- 1. Аналитический способ сложение сил (метод проекций).
- 2. Равновесие системы сходящихся сил.
- 3. Теорема о трех силах.
- 4. Реакции геометрических связей.
- Силы в теоретической механике
- Основные понятия и аксиомы статики
- Основные определения
- Аксиомы статики
- Связи и их реакции
- Сложение сил. Система сходящихся сил
- Сложение двух сил
- Сложение системы сил
- Разложение сил
- Аналитический способ задания сил
- Аналитический способ сложения сил
- Равновесие плоской системы сходящихся сил
- Момент силы относительно центра или точки
- Теорема Вариньона о моменте равнодействующей
1. Аналитический способ сложение сил (метод проекций).
2. Равновесие системы сходящихся сил.
3. Теорема о трех силах.
4. Реакции геометрических связей.
Порядок решения задач статики.
1. Метод проекций, с помощью которого реализуется аналитический способ сложения любого числа сил, основан на применении следующей теоремы геометрии: проекция векторной суммы на любую ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Рис. 1.10. Иллюстрация метода проекций
Пусть 

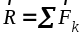
Rx = Fkx , Ry = Fky , 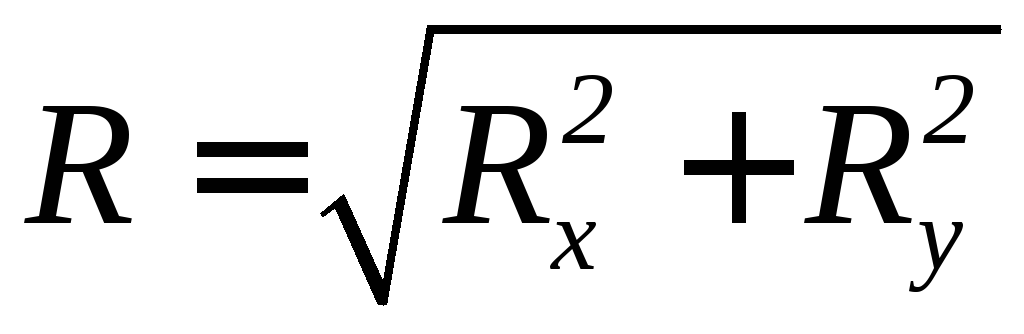
В пространственном случае
Rx = Fkx , Ry = Fky , Rz = Fkz , 
Равновесие системы сходящихся сил
Геометрическая сумма произвольной системы сил называется главным вектором этой системы сил, т.е.:

Понятие главного вектора нельзя путать с понятием равнодействующей. Равнодействующая — это сила, эквивалентная по действию на тело всей системе сил, с вполне определенной линией действие. Главный вектор — это формально вычисленная геометрическая сумма всех сил системы и, являясь свободным вектором, может быть приложена в любой точке тела. Но если некоторая система имеет равнодействующую, то она численно равна и параллельна главному вектору этой системы. Например, к таким системам относятся все системы сходящихся сил.
Для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая (а, следовательно и главный вектор данной системы сил) были равны нулю.
Условия, которым при этом должны удовлетворять силы системы, можно выразить в геометрической и в аналитической форме.
Геометрические условия равновесия.
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из сил системы, был замкнутым. Это означает равенство нулю равнодействующей и главного вектора данной системы сил. Напомним, что векторная сумма — это вектор, соединяющий конец последнего из слагаемых векторов с началом первого из них.
Аналитические условия равновесия.
Очевидно [см. формулы (1.1)], что равнодействующая системы сходящихся сил и ее главный вектор будут равны нулю, если суммы проекций всех сил на координатные оси будут равны нулю, т.е.
Равенства (1.2) выражают условия равновесия системы сходящихся сил в аналитической форме.
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Так как по условию теоремы все три силы непараллельны, перенесем две любые из них в точку пересечения их линий действий (на рис 1.11 силы А! и А@ переносятся в точку Е) и заменим равнодействующей ™. Поскольку тело по условию находится в равновесии, а операция по переносу сил вдоль линий их действия и последующего сложения этого равновесия не нарушит, то линия действия третьей силы А# должна пройти через точку Е в соответствие с первой аксиомой статики.
Рис. 1.11. К доказательству теоремы о трех силах
Реакции геометрических связей
Сила, с которой данная связь действует на тело, препятствуя его перемещению, называется силой реакции связи или просто реакцией связи. Значения реакций связей определяются в процессе решения соответствующей задачи механики. Направлена же реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Ниже представлены наиболее часто встречающиеся типы связей и направления их реакций.
Гладкая плоскость (поверхность или опора)(рис. 1.12). Реакция 
Нить (канат, цепь, ремень, трос).Связь, осуществленная в виде гибкой нерастяжимой нити (рис. 1.13), не дает телуМ удаляться от точки подвеса нити по направлениюАМ.Поэтому реакция 
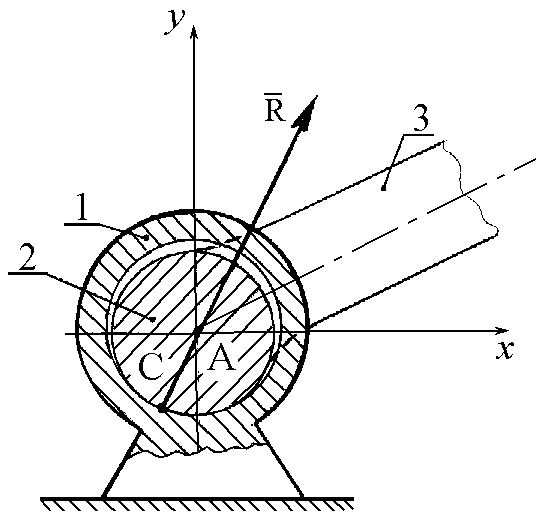
Неподвижный цилиндрический шарнир или подшипник (шарнирно-неподвижная опора).Цилиндрическим шарниром (рис. 1.14) называется совокупность неподвижной обоймы (втулки)1и помещенного в нее валика (пальца)2, жестко соединенного с телом3. В точкеСсоприкосновения втулки с валиком возникает сила опорной реакции, направленная по нормали к идеально гладким поверхностям. Эта нормаль проходит через геометрический центрАвалика. Так как положение точкиСсоприкосновения валика со втулкой заранее не известно, то невозможно сразу указать направление силы реакции 





Рис. 1.14 Рис. 1.15

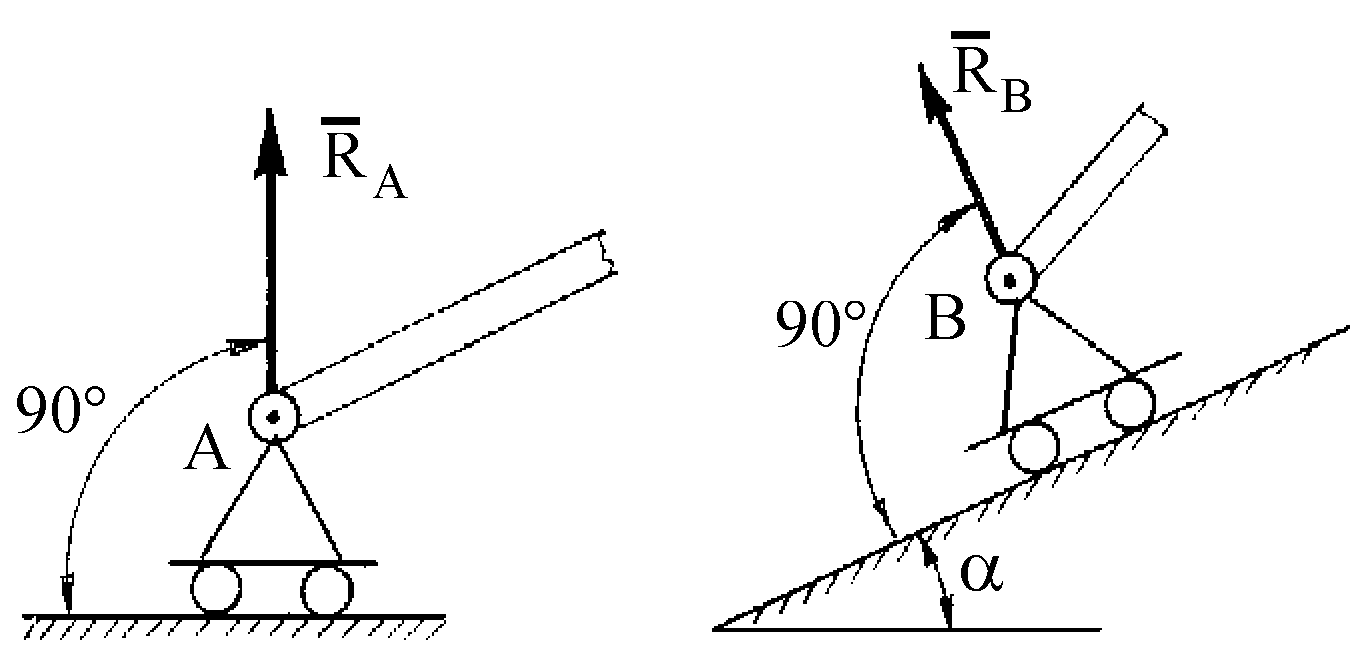
Шарнирно-подвижная опора (опора на катках).Реакция 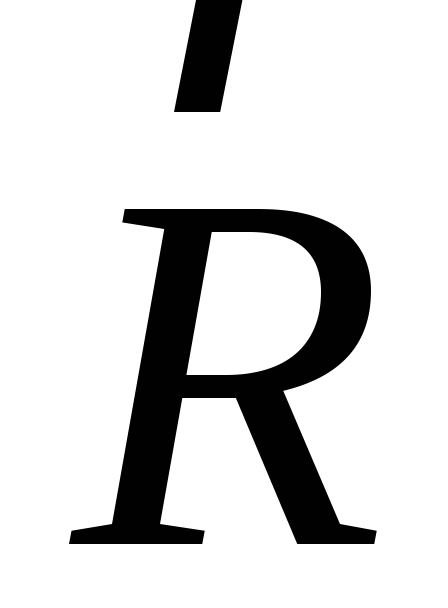
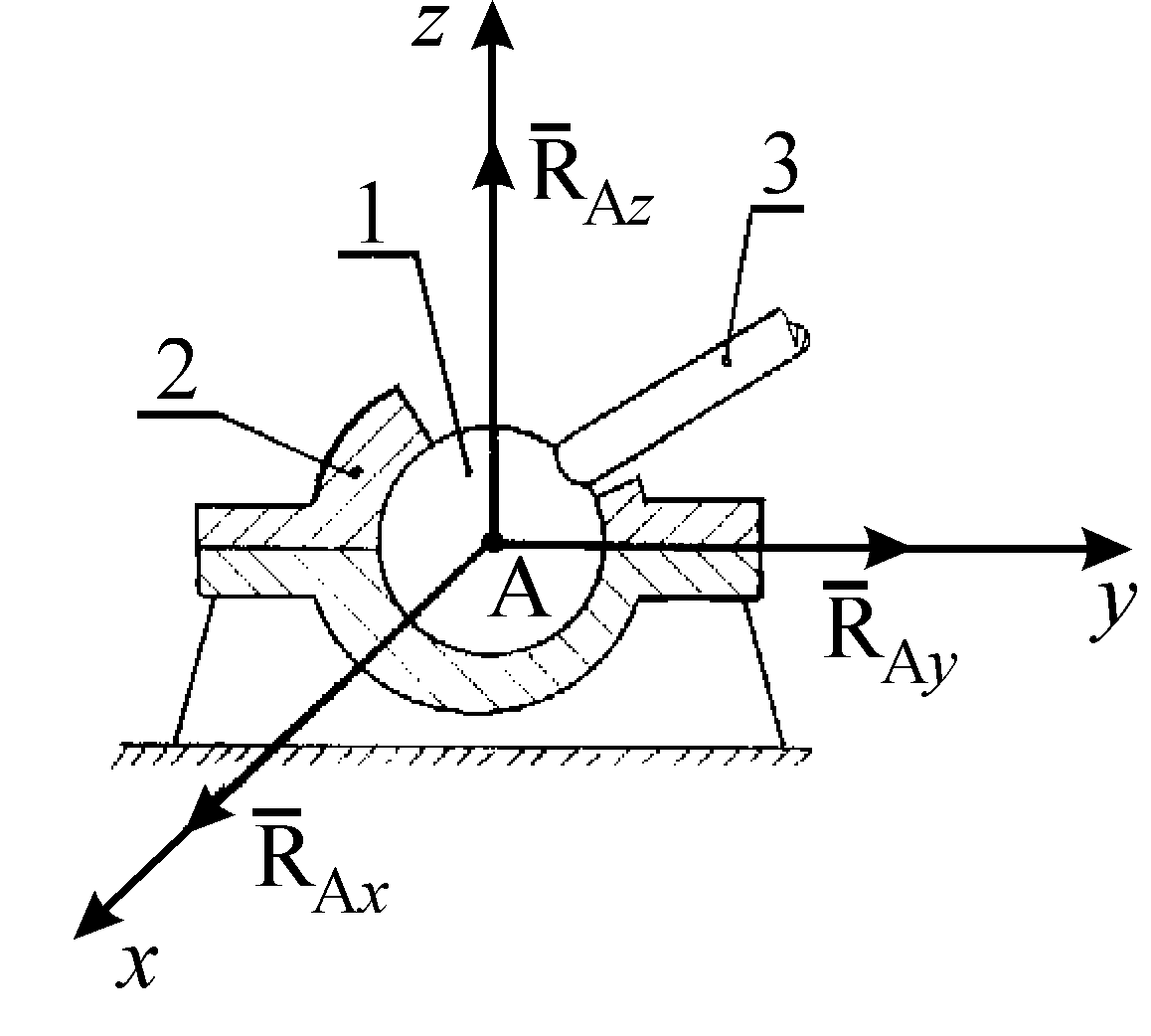
Сферический шарнир(рис. 1.17). Сферическим шарниром называется устройство, выполненное в виде двух контактирующих сфер, геометрический центрАкоторых неподвижен. Тело3, равновесие которого рассматривается, жестко связано с внутренней подвижной сферой1. При условии, что сферические поверхности гладкие, реакция 
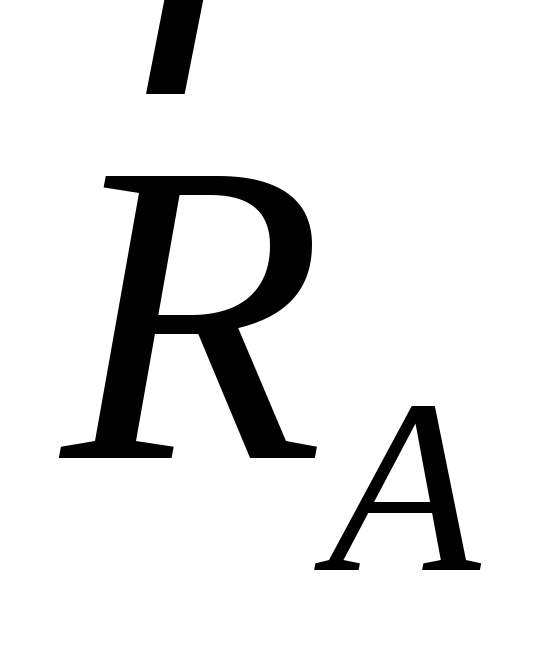


Подпятник (рис. 1.18). Подпятник представляет собой соединение цилиндрического шарнира 2 и опорной плоскости 3, на которую опирается вал 1. Реакция подшипника, лежащая в плоскости перпендикулярной оси вала, представляется двумя ее взаимно-перпендикулярными составляющими 


Невесомый стержень(рис. 1.19). Реакция 
Жесткая заделка (неподвижное защемление)конца балки (рис. 1.20). Такая связь не допускает не только линейных перемещений балки1вдоль координатных осей, но и вращения балки в плоскостихАу.
Нахождение реакций жесткой заделки сводится к определению трех неизвестных величин: составляющих 


5. Порядок решения задач статики
Большинство задач статики решаются в следующем порядке:
а). Для решения задачи нужно рассмотреть равновесие твердого тела, к кото-
рому приложены заданные и искомые силы (или силы равные искомым).
б). На чертеже изображаем все силы, приложенные к данному телу, включая
в). Выбираем систему координат и составляем уравнения равновесия.
г) Решая данную систему уравнений равновесия, определяем искомые величины.
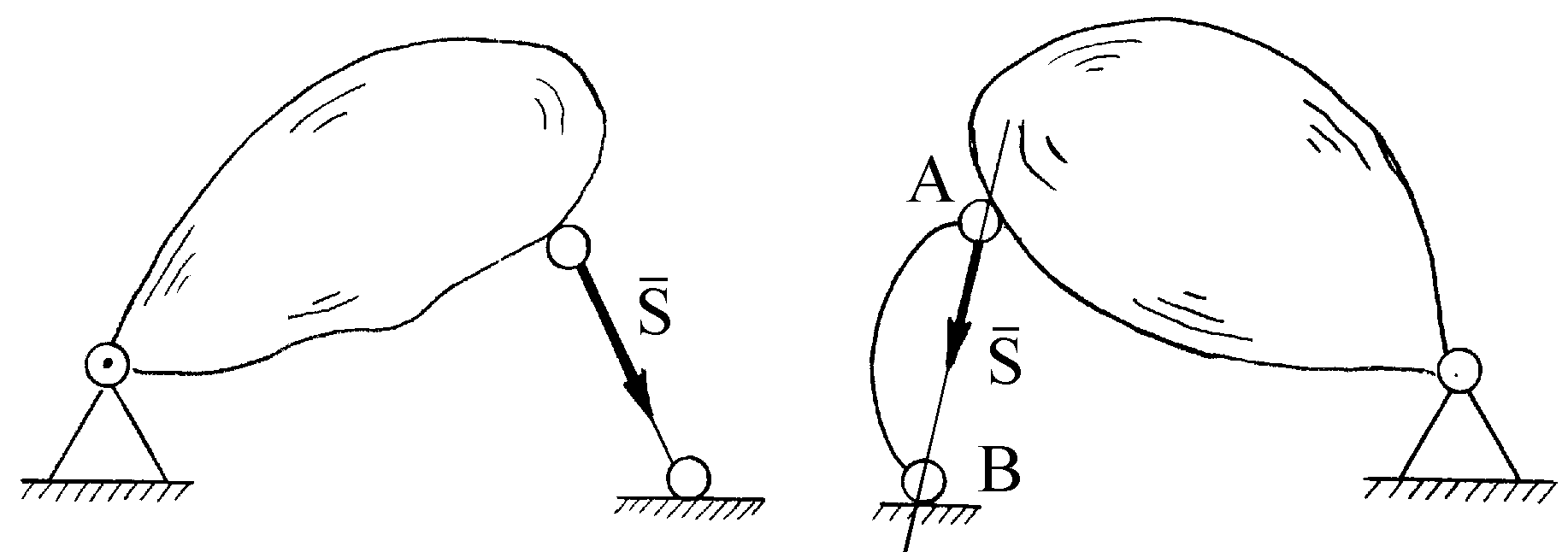
Пример. Однородная балка АС длиной L = 3 м и весом P= 40 кН поднимается вверх с помощью крана. Определить минимальную длину троса АВС, при котором возможен подъем балки, если трос выдерживает натяжение T = 30 кН.
Решение. Рассмотрим равновесие балки, поскольку именно к ней приложены заданная сила (вес балки) и силы натяжения троса. Пусть оси системы координат направлены как обычно: ось x вправо, ось y — вверх. Тогда уравнения равновесия запишутся в виде:
Подставляя во второе уравнение численные значения веса Р и максимальное значение силы натяжения Т, определяем значение sin, а затем и минимальную длину троса:
Источник
Силы в теоретической механике
Содержание:
Основные понятия и аксиомы статики
Под равновесием понимается состояние покоя тела по отношению к другим материальным телам.
Абсолютно твердое тело — это тело, расстояние между любыми двумя точками которого всегда остается постоянным.
Чтобы твердое тело под действием некоторой системы сил находилось в равновесии (в покое), необходимо, чтобы эти силы удовлетворяли определенным условиям равновесия данной системы сил.
Основными задачами статики являются:
- 1. Сложение сил и приведение системы сил, действующих на твердое тело, к простейшему виду.
- 2. Определение условий равновесия систем сил, действующих на твердое тело.
Состояние равновесия или движение тела зависит от характера его механических взаимодействий с другими телами.
Сила — это величина количественной меры механического взаимодействия материальных тел.
Рассматриваемые в механике величины разделяют на векторные и скалярные.
Скалярные величины характеризуются только численными значениями.
Векторные величины характеризуются численными значениями и направлением в пространстве.
Сила является векторной величиной и ее действие на тело определяется численной величиной, или мерой силы, направлением силы, точкой приложением силы.
Сила (в механике) измеряется в Ньютонах (
Основные определения
Прямая, вдоль которой направлена сила, называется линией действия силы.
Совокупность сил, действующих на какое-либо тело называется системой сил.
Тело, не связанное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.
Если одну систему сил, действующую на тело, можно заменить другой системой, не изменяя при этом состояние данной системы, то такие две системы сил называются эквивалентными.
Система сил, под действием которой свободное твердое тело может находиться в покос, называется уравновешенной или эквивалентной нулю.
Равнодействующая сила — это сила, которая одна заменяет действие данной системы сил на твердое тело.
Сила, равная равнодействующей силе по модулю, но противоположно направленная по той же прямой, называется уравновешивающей.
Силы бывают внешними и внутренними:
Внешние силы действуют со стороны других материальных тел.
Внутренние — это силы, с которыми частицы данного тела действуют друг на друга.
Сила, приложенная к телу в какой-либо точке, называется сосредоточенной.
Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.
Возможно вам будут полезны данные страницы:
Аксиомы статики
Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств. Эти положение называются аксиомами статики.
- Аксиома 1. Если на свободное, абсолютно твердое тело действуют две силы, то твердое тело может находиться в равновесии тогда и только тогда, когда эти силы будут равны по модулю (
) и направлены вдоль одной прямой в противоположные стороны (рис. 1.1). Следовательно, тело, на которое действует только одна сила, находиться в равновесии не может.
- Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней прибавить или отнять уравновешивающую систему сил.
Следствие из 1-й и 2-й аксиом таково: действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
Этим принципом можно пользоваться тогда, когда определяются условия равновесия той или иной конструкции и не рассматриваются возникающие в ее частях внутренние усилия. Следовательно, при определении внутренних усилий переносить точку приложения силы вдоль линии действия нельзя.
- Аксиома 3. Две силы, приложенные к телу в одной точке, имеют равнодействующую, изображаемую диагональю параллелограмма, построенную на этих силах как на сторонах (рис. 1.2).
- Аксиома 4. При всяком действии силы материального тела на другое имеет место такое же по величине, противоположное по направлению противодействие (рис. 1.3).
- Аксиома 5. Равновесие деформируемого тела, находящегося под действием данной системы сил, не нарушится, если тело считать абсолютно твердым.
Связи и их реакции
Тело, которое из данного положения может совершать любые перемещения в пространстве, называется свободным.
Тело, перемещению которого препятствуют другие скрепленные или соединенные с ним тела, называется несвободным.
Все то, что ограничивает перемещение данного тела в пространстве, называется связью.
Сила, с которой данная связь действует на тело, препятствуя его перемещениям, называется реакцией связи.
Реакция связи направлена в сторону, противоположную той, куда связь не даст перемещаться телу (при решении задач очень важно правильно определить направление реакций связи).
1. Гладкая поверхность или опора. Реакция 
2. Нить. Реакция 
3. Цилиндрический шарнир. Реакция 
4. Шаровой шарнир и подпятник. Реакция 
Аксиома связей. Всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями этих связей (рис. 1.8).
Реакции связи — это исходные данные, которые необходимо знать при расчете конструкций на прочность.
Сложение сил. Система сходящихся сил
Величина геометрической суммы сил называется главным вектором системы сил. Геометрическая сумма — это нсравнодсйствующая сил, т.е. для многих систем равнодействующих вообще не существует, а геометрическую сумму можно вычислить для любой системы сил.
Сложение двух сил
Геометрическая сумма 


Модуль 


где 
Углы 


Сложение системы сил
Правило параллепипеда. Геометрическая сумма 


Геометрическая сумма любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Рассмотрим второй способ как наиболее простой.
Для нахождения суммы сил 
Необходимо учесть, что при построении векторного многоугольника у всех векторов стрелки должны быть направлены в одну сторону, а у вектора 
Сходящимися называются силы, линии действия которых пересекаются в одной точке.
Последовательно применяя аксиому параллелограмма сил, получаем, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору 
Разложение сил
Разложение сил — это разложение равнодействующей силы на систему сил. Эта задача является неопределенной и имеет однозначное решение лишь при задании дополнительных условий.
Разложение силы по двум заданным направлениям. Для того чтобы разложить силу 
Например, по направлению прямых 


Разложение силы по трем заданным направлениям. Решение этой задачи сводится к построению такого параллепипеда, у которого диагональю является данная сила 
Пример. Кронштейн состоит из стержней 









Из треугольника 
Из того же треугольника найдем, что стержень 
Далее рассмотрим проекцию силы на ось и на плоскость.
Проекцией силы на ось называется скалярная величина, равная величине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, сели перемещение от ее начала к концу происходит в положительном направлении оси (совпадает по направлению), и знак минус, если в отрицательном (рис. 1.13).
Из вышесказанного определения следует, что проекции силы на любые параллельные и одинаково направленные оси равны друг другу.
Проекции силы на ось записываются с индексом, соответствующим данной оси:
На рисунке видно, что
Проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси.
Проекция силы будет положительной, если этот угол — острый, и отрицательной, если тупой.
Если сила перпендикулярна к оси, то ее проекция на ось равна нулю. Проекцией силы на плоскость 


Проекция силы на плоскость есть величина векторная, так как она характеризуется численным значением и направлением в плоскости (рис. 1.14):
Аналитический способ задания сил
Для аналитического задания силы необходимо выбрать систему координатных осей 
Величины модуля силы 



Для решения задач статики более удобно задавать силу ее проекциями:
Возведя равенство 1 почленно в квадрат и складывая их получим
Когда все рассматриваемые силы лежат в одной плоскости, то каждую из сил можно задать се проекциями на две оси 
Аналитический способ сложения сил
Сложение сил. Переход от зависимостей между векторами к зависимостям между их проекциями осуществляется с помощью следующей теоремы геометрии: проекция вектора силы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось (рис. 1.16).
Если вектор силы
где
Для любой системы сил равнодействующая (или главный вектор 

Зная 
Формулы (1.1) и (1.2) позволяют решить задачу о сложении сил аналитически. Для сил, лежащих в одной плоскости, формулы (1.1) и (1.2) примут вид
Равновесие плоской системы сходящихся сил
Твердое тело, на которое действуют взаимно уравновешивающие внешние силы, может не только находиться в покое, но и совершать движение «по инерции». Например, поступательное равномерное или прямолинейное движение тела. Отсюда можно сделать следующие выводы:
- 1. Условиям равновесия статики удовлетворяют силы, действующие как на покоящееся тело, так и на тело, движущееся «по инерции».
- 2. В покос тело будет находиться лишь в том случае, если оно было в покос и до момента приложения к нему уравновешенных сил.
- 3. Для равновесия приложенной к твердому телу системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сил была равна нулю.
- 4. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или аналитической форме.
Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.
Аналитическое условие равновесия. Так как 

Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух координатных осей были равны нулю:
Теорема о трех силах. Если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил должны пересекаться в одной точке.
При решении задач о равновесии несвободного тела реакции наложенных связей являются величинами неизвестными. Соответствующая задача статики может быть решена только тогда, когда число неизвестных реакций связей не превышает числа уравнений равновесия, содержащих эти реакции. Такие задачи называются статически определимыми.
Задачи, в которых число неизвестных реакций связей больше числа уравнений равновесия, содержащих эти реакции, называются статически неопределимыми (рис. 1.17).
Например, груз подвешен на трех стержнях. В этом случае для плоской системы сходящихся сил можно составить только два уравнения равновесия, а неизвестных усилий будет три. Поэтому данная система статически неопределима.
Момент силы относительно центра или точки
Под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра.
Вращательный эффект силы характеризуется ее моментом.
Моментом силы 




Правило знаков для момента. Момент имеет знак плюс, если сила стремится повернуть тело против хода часовой стрелки.
Момент имеет знак минус, если сила стремится повернуть тело по ходу часовой стрелки.
Основные свойства момента силы:
- 1. Момент силы не изменится при переносе точки приложения силы вдоль ее линии действия.
- 2. Момент силы относительно центра
равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр
(плечо равно нулю).
Теорема Вариньона о моменте равнодействующей
Момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Аналитические условия равновесия сходящихся сил можно выразить не только через проекции этих сил, но и через моменты (рис. 1.19). На основании теоремы Вариньона можно записать еще одну форму условий равновесия плоской системы сходящихся сил:
где 


На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Услуги по теоретической механике:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Источник












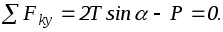

 ) и направлены вдоль одной прямой в противоположные стороны (рис. 1.1). Следовательно, тело, на которое действует только одна сила, находиться в равновесии не может.
) и направлены вдоль одной прямой в противоположные стороны (рис. 1.1). Следовательно, тело, на которое действует только одна сила, находиться в равновесии не может.












































 равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр
равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр  (плечо равно нулю).
(плечо равно нулю).







