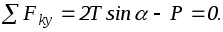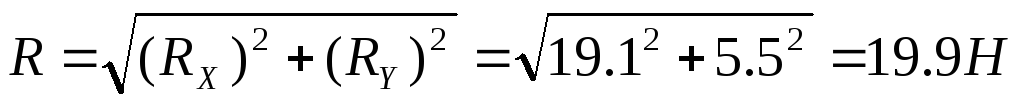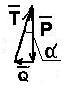1. Аналитический способ сложение сил (метод проекций).
2. Равновесие системы сходящихся сил.
3. Теорема о трех силах.
4. Реакции геометрических связей.
Порядок решения задач статики.
1. Метод проекций, с помощью которого реализуется аналитический способ сложения любого числа сил, основан на применении следующей теоремы геометрии: проекция векторной суммы на любую ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Рис. 1.10. Иллюстрация метода проекций
Пусть 

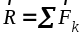
Rx = Fkx , Ry = Fky , 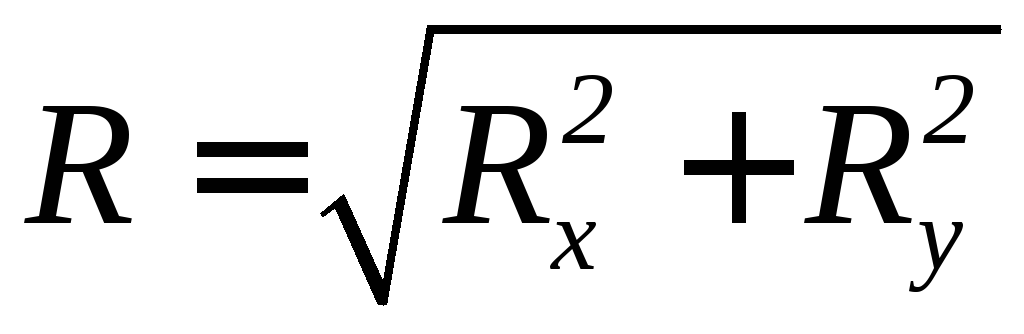
В пространственном случае
Rx = Fkx , Ry = Fky , Rz = Fkz , 
Равновесие системы сходящихся сил
Геометрическая сумма произвольной системы сил называется главным вектором этой системы сил, т.е.:

Понятие главного вектора нельзя путать с понятием равнодействующей. Равнодействующая — это сила, эквивалентная по действию на тело всей системе сил, с вполне определенной линией действие. Главный вектор — это формально вычисленная геометрическая сумма всех сил системы и, являясь свободным вектором, может быть приложена в любой точке тела. Но если некоторая система имеет равнодействующую, то она численно равна и параллельна главному вектору этой системы. Например, к таким системам относятся все системы сходящихся сил.
Для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая (а, следовательно и главный вектор данной системы сил) были равны нулю.
Условия, которым при этом должны удовлетворять силы системы, можно выразить в геометрической и в аналитической форме.
Геометрические условия равновесия.
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из сил системы, был замкнутым. Это означает равенство нулю равнодействующей и главного вектора данной системы сил. Напомним, что векторная сумма — это вектор, соединяющий конец последнего из слагаемых векторов с началом первого из них.
Аналитические условия равновесия.
Очевидно [см. формулы (1.1)], что равнодействующая системы сходящихся сил и ее главный вектор будут равны нулю, если суммы проекций всех сил на координатные оси будут равны нулю, т.е.
Равенства (1.2) выражают условия равновесия системы сходящихся сил в аналитической форме.
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Так как по условию теоремы все три силы непараллельны, перенесем две любые из них в точку пересечения их линий действий (на рис 1.11 силы А! и А@ переносятся в точку Е) и заменим равнодействующей ™. Поскольку тело по условию находится в равновесии, а операция по переносу сил вдоль линий их действия и последующего сложения этого равновесия не нарушит, то линия действия третьей силы А# должна пройти через точку Е в соответствие с первой аксиомой статики.
Рис. 1.11. К доказательству теоремы о трех силах
Реакции геометрических связей
Сила, с которой данная связь действует на тело, препятствуя его перемещению, называется силой реакции связи или просто реакцией связи. Значения реакций связей определяются в процессе решения соответствующей задачи механики. Направлена же реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Ниже представлены наиболее часто встречающиеся типы связей и направления их реакций.
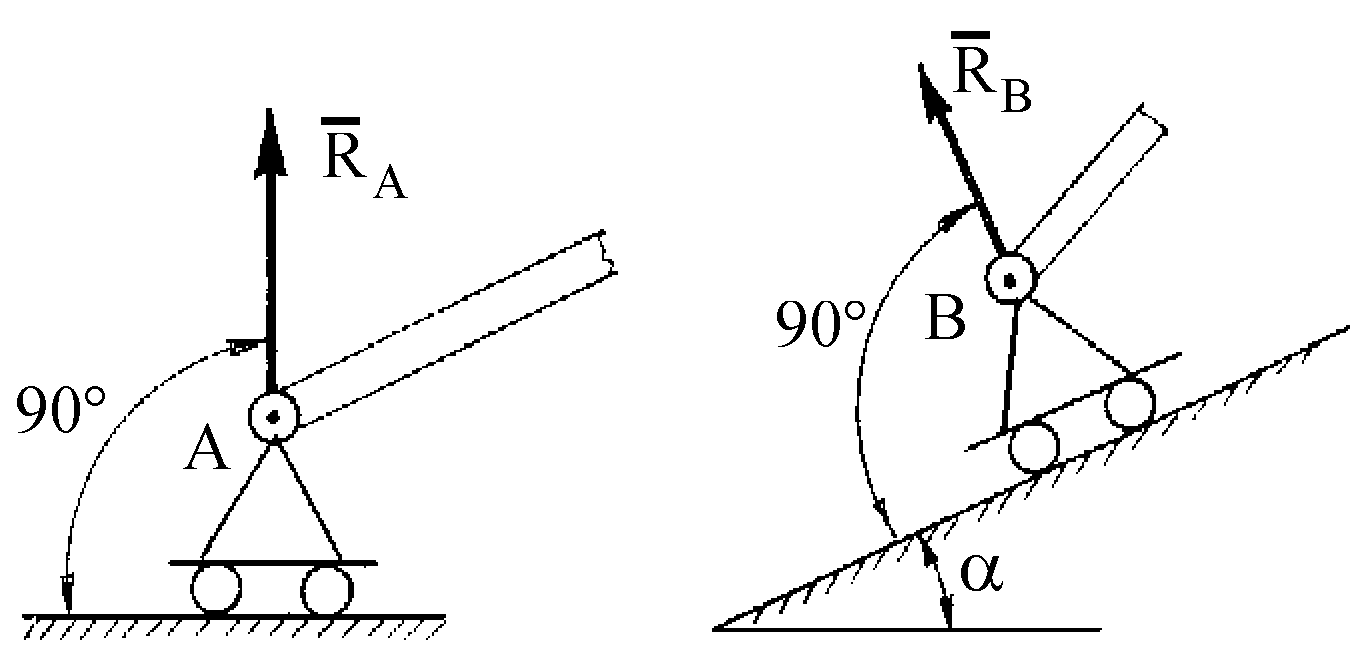
Гладкая плоскость (поверхность или опора)(рис. 1.12). Реакция 
Нить (канат, цепь, ремень, трос).Связь, осуществленная в виде гибкой нерастяжимой нити (рис. 1.13), не дает телуМ удаляться от точки подвеса нити по направлениюАМ.Поэтому реакция 
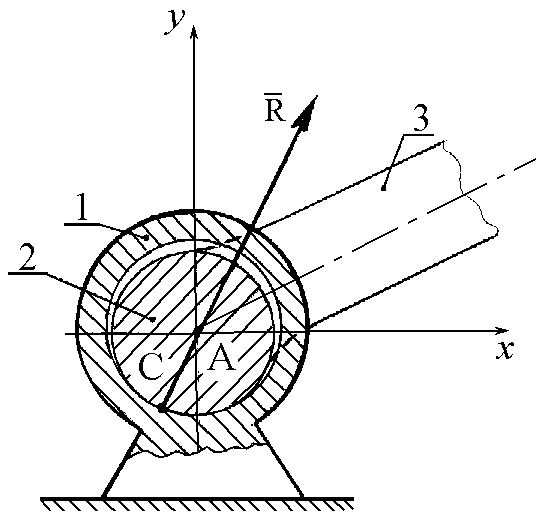
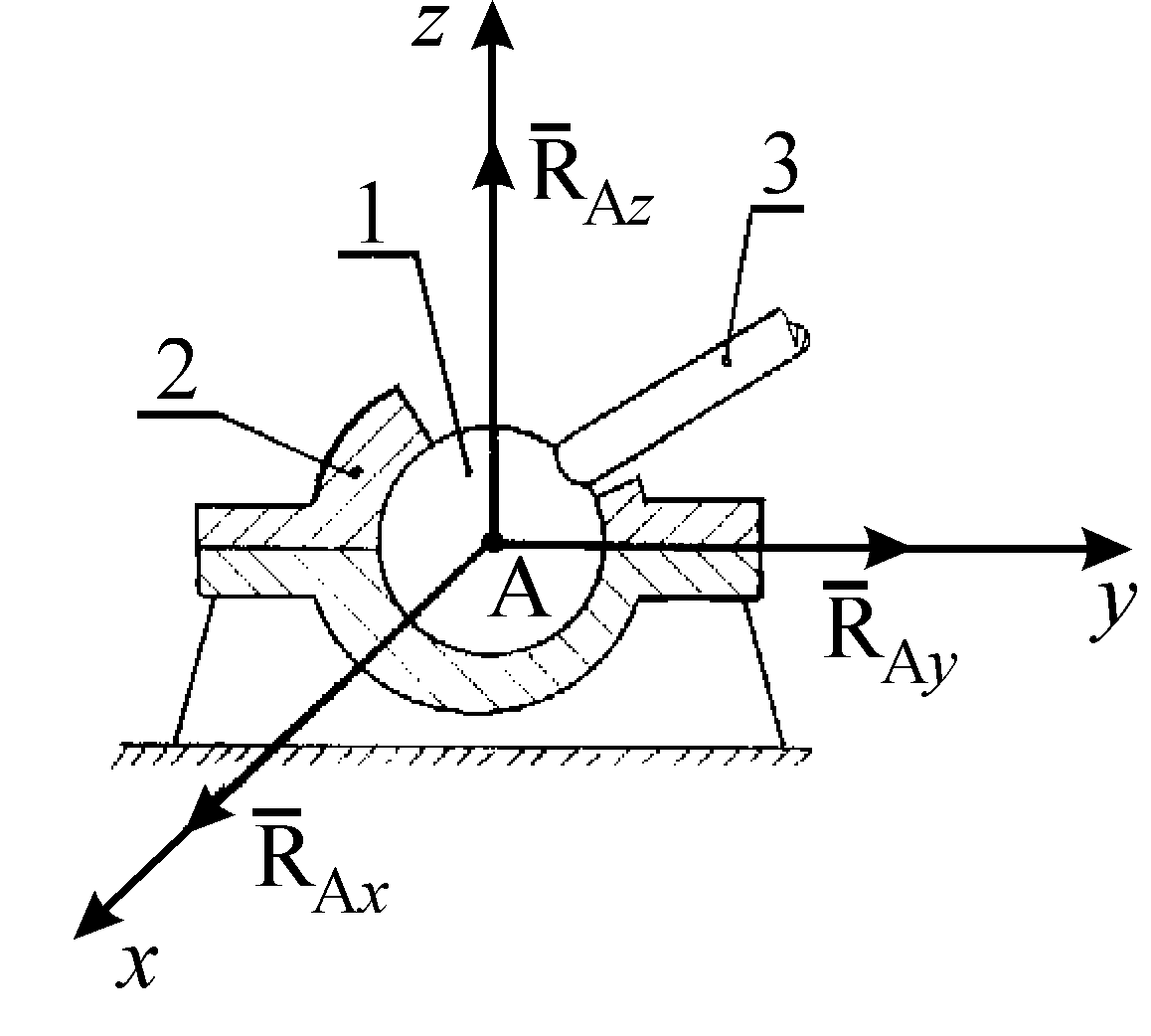
Неподвижный цилиндрический шарнир или подшипник (шарнирно-неподвижная опора).Цилиндрическим шарниром (рис. 1.14) называется совокупность неподвижной обоймы (втулки)1и помещенного в нее валика (пальца)2, жестко соединенного с телом3. В точкеСсоприкосновения втулки с валиком возникает сила опорной реакции, направленная по нормали к идеально гладким поверхностям. Эта нормаль проходит через геометрический центрАвалика. Так как положение точкиСсоприкосновения валика со втулкой заранее не известно, то невозможно сразу указать направление силы реакции 





Рис. 1.14 Рис. 1.15

Шарнирно-подвижная опора (опора на катках).Реакция 
Сферический шарнир(рис. 1.17). Сферическим шарниром называется устройство, выполненное в виде двух контактирующих сфер, геометрический центрАкоторых неподвижен. Тело3, равновесие которого рассматривается, жестко связано с внутренней подвижной сферой1. При условии, что сферические поверхности гладкие, реакция 

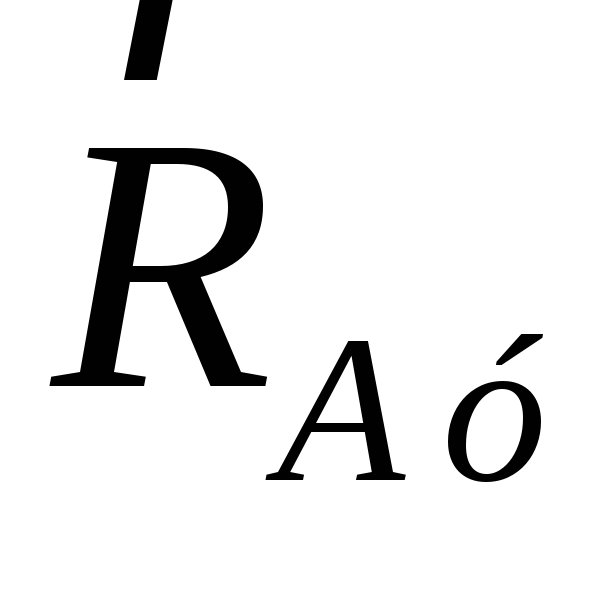

Подпятник (рис. 1.18). Подпятник представляет собой соединение цилиндрического шарнира 2 и опорной плоскости 3, на которую опирается вал 1. Реакция подшипника, лежащая в плоскости перпендикулярной оси вала, представляется двумя ее взаимно-перпендикулярными составляющими 


Невесомый стержень(рис. 1.19). Реакция 
Жесткая заделка (неподвижное защемление)конца балки (рис. 1.20). Такая связь не допускает не только линейных перемещений балки1вдоль координатных осей, но и вращения балки в плоскостихАу.
Нахождение реакций жесткой заделки сводится к определению трех неизвестных величин: составляющих 


5. Порядок решения задач статики
Большинство задач статики решаются в следующем порядке:
а). Для решения задачи нужно рассмотреть равновесие твердого тела, к кото-
рому приложены заданные и искомые силы (или силы равные искомым).
б). На чертеже изображаем все силы, приложенные к данному телу, включая
в). Выбираем систему координат и составляем уравнения равновесия.
г) Решая данную систему уравнений равновесия, определяем искомые величины.
Пример. Однородная балка АС длиной L = 3 м и весом P= 40 кН поднимается вверх с помощью крана. Определить минимальную длину троса АВС, при котором возможен подъем балки, если трос выдерживает натяжение T = 30 кН.
Решение. Рассмотрим равновесие балки, поскольку именно к ней приложены заданная сила (вес балки) и силы натяжения троса. Пусть оси системы координат направлены как обычно: ось x вправо, ось y — вверх. Тогда уравнения равновесия запишутся в виде:
Подставляя во второе уравнение численные значения веса Р и максимальное значение силы натяжения Т, определяем значение sin, а затем и минимальную длину троса:
Источник
Аналитический способ сложения сил
Теорема: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Е
Модуль результирующей силы:
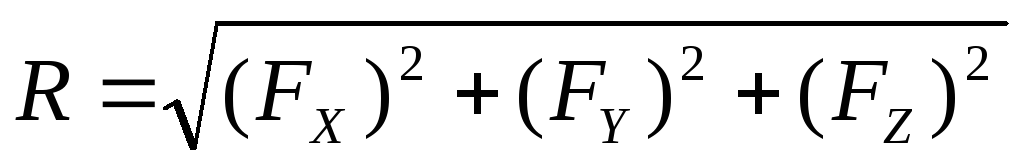
Н
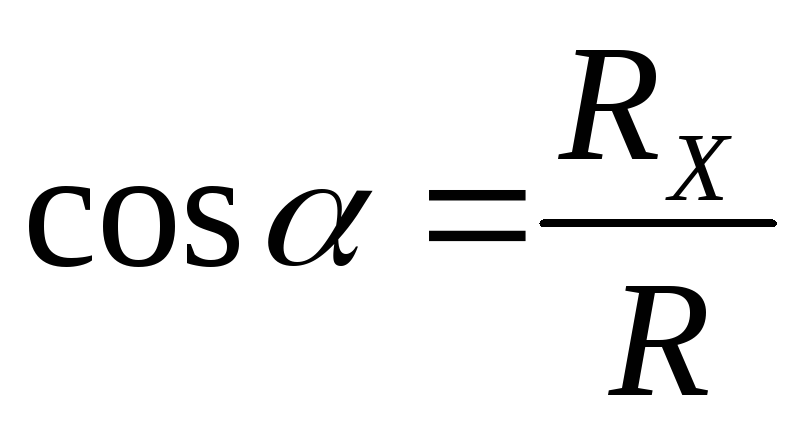
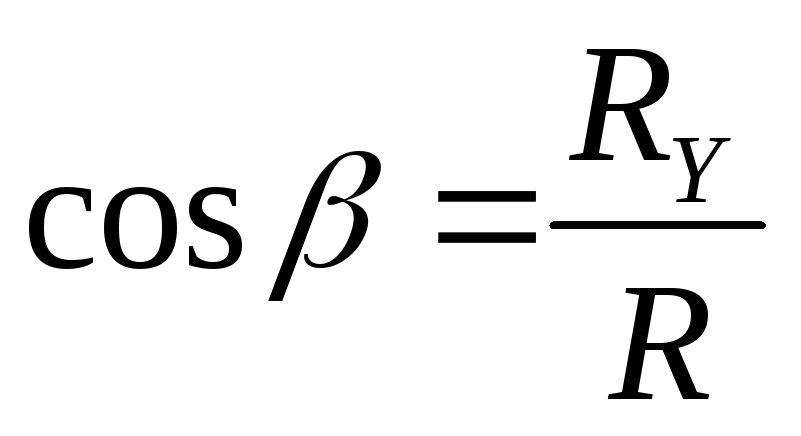

П
Р
Rx = 3 + 6 – 5 = 4H; Ry = 3 – 2 – 3 = -2H;
одуль результирующей силы:
Ответ: R = 4,5H; = 63 o ; = 27 o .
Пример 2. Задана плоская система сил, действующая на точку А. F1 = 15Н; F2 = 10Н. Определить равнодействующую силу (рис. 2.5).
Р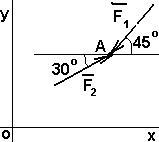
Определим сумму проекций данных сил на оси OX и OY:
Ось OX:
сьOY:
Подставляя численные значения получим:
Модуль равнодействующей:
Направляющие косинусы: 

Ответ: R = 19,9H; = 74 o ; = 16 o .
Равновесие системы сходящихся сил
Система сходящихся сил – это силы, сходящиеся в одной точке (рис. 2.6).
Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.
А
налитические условия равновесия. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.
Теорема о трех силах. Если свободное твердое тело находится в состоянии равновесия под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
F
Системы статически определимые и статически неопределимые
Задача статики может быть решена лишь в том случае, когда для нее число неизвестных реакций связей не превышает число уравнений равновесия, содержащих эти реакции. Такие задачи называют статически определенные, а система тел, для которых это имеет место – статически определимыми системами.
Задачи, в которых число неизвестных реакций связей больше числа уравнений равновесия, содержащих эти реакции, называются статически неопределенные, а система тел для которых это имеет место – статически неопределимыми системами.
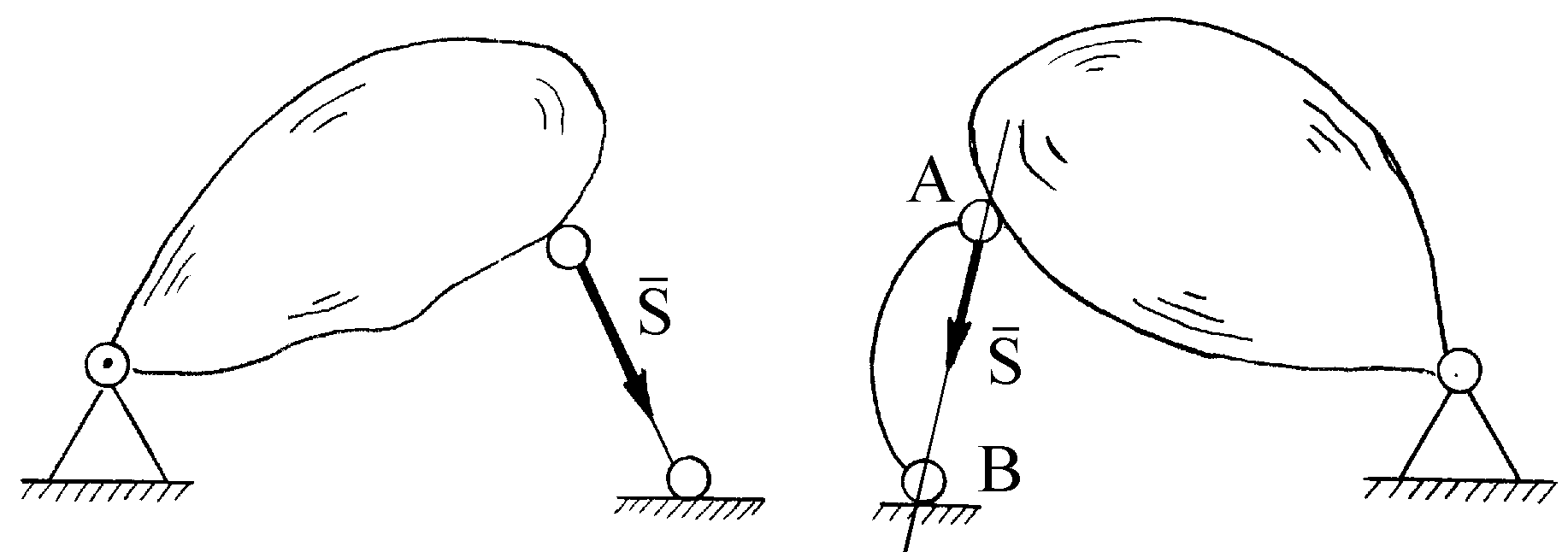
П
римером для статически неопределенной системы может служить груз, подвешенный на трех нитях, лежащих в одной плоскости (рис. 2.7). В этой задаче три неизвестные силы натяжения нитиT1, T2, T3, а уравнений равновесия в случае плоской системы сходящихся сил можно составить только два.
Решение задач статики
Для решения задач статики необходимо:
Выбрать тело, равновесие которого должно быть рассмотрено.
Освобождение тела от связей и изображение действующих на него заданных сил и реакций отброшенных связей.
Составление уравнений равновесия.
Определение искомых величин, проверка правильности решения и исследование полученных результатов.
Для решения задач на равновесие тела под действием сходящихся сил можно использовать следующие способы:
а
б) Аналитический способ. Применяется при любом количестве сил, действующих на тело. В случае плоской системы сходящихся сил составляется два уравнения равновесия, а в случае пространственной системы сил – три.
П
Р
Силовой треугольник должен быть замкнут. В данном случае это прямоугольный треугольник. Тогда: 
твет:
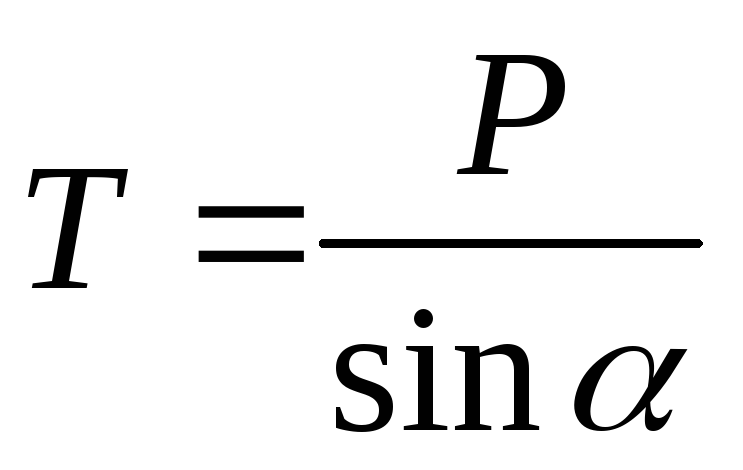
ример №4. Однородный стержень АВ прикреплен к стенке посредством шарнира А и удерживается под углом 60 0 к вертикали при помощи троса ВС, образующего с ним угол 30 0 (рис. 2.9а). Определить величину и направление реакции R шарнира, если известно, что вес стержня равен 20Н.
Определим силы, действующие на данную конструкцию:
Р – сила тяжести стержня АВ, так как стержень однородный, то сила приложена к его геометрическому центру (точка О).
Т – натяжение троса СВ, направлено вдоль СВ.
R – реакция в шарнире А (направление неизвестно) (рис. 2.9б).
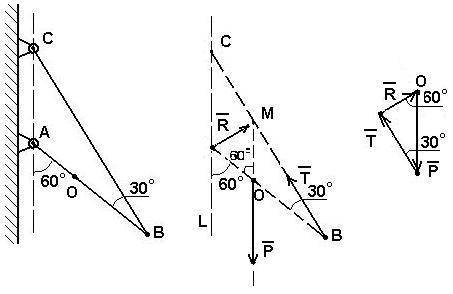
Согласно принципу освобождаемости от связей, заменим связи соответствующими реакциями.
Так как система находится в равновесии под действием трех сил, то эти силы должны сходиться, а поэтому сила реакции R направлена от А к М (точка пересечения сил Р и Т).
Построим силовой треугольник. Для этого выберем произвольную точку О и отложим от нее известную силу Р, сохраняя ее направление. Из конца вектора Р под углом 30 0 проведем луч, который соответствует направлению силы Т (рис. 2.9в).
Так как — 60 0 = 120 0 , тогда 0 – (120 0 + 30 0 ) = 30 0 , т.е. треугольник ОМВ равнобедренный: сторона ОМ = ОВ. Поэтому ОМ = ОВ = ОА, так как О является серединой АВ, а угол 0 , то треугольник АОМ является равносторонним. Поэтому 0 = 0 к направлению силы Р до пересечения с направлением силы Т. Полученный треугольник прямоугольный, поэтому R = Psin30 0 = 20/2 = 10H.
Пример №5. Три груза А, В и С массой 10, 20, и 60 кг соответственно лежат на плоскости, наклоненной под углом к горизонту (рис. 2.10). Грузы соединены тросами, как показано на рисунке. Коэффициенты трения между грузами и плоскостью равны А = 0,1, В = 0,25, С = 0,5 соответственно.
Определить угол , при котором тела равномерно движутся вниз по плоскости. Найти также натяжение тросов ТАВ и ТВС.
Р
ассмотрим, какие силы действуют на каждое тело и запишем условие равновесия, так как тела движутся равномерно, то
с
Выберем систему координат и спроектируем силы на оси:
Подставляя численные значения получим: 10sin — cos — ТАВ = 0.
Р
Проектируя это уравнение на ось ОХ, получим:
Н
60sin — 60*0,5cos – ТВС = 0.
Получим систему из трех уравнений с тремя неизвестными:
Так как неизвестные силы перпендикулярны оси y, то на эту ось силы не проектируем.
1
60sin — 30cos – ТВС = 0 (3).
Отсюда: ТАВ = 10sin — cos; ТВС = 60sin — 30cos.
Подставляя выражения ТАВ и ТВС в уравнение (2), получим:
100sin = 38.5cos; tg = 0.385; = arctg0.385; = 21 0 .
Из уравнения (1) получим: ТАВ = 10sin21 0 — cos21 0 = 10*0,358 – 0,93 = 2,67Н.
Подставляя численные данные в уравнение (3), получим:
ТВС = 60sin21 0 — 30cos21 0 = 60*0,358 – 30*0,93 = 6,42Н;
Ответ: = 21 0 ; ТАВ = 2,67Н; ТВС = 6,42Н.
Источник