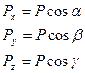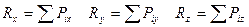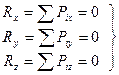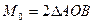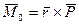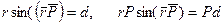Геометрический и аналитический способы сложения сходящихся сил.
Основные определения и понятия статики. Проецирование силы на ось.
Равновесие- такое состояние, при котором тело находится в покое или движется равномерно и прямолинейно.
Твердое тело-такое тело, расстояние между каждыми двумя точками которого всегда остается постоянным.
Материальная точка-тело, размерами которого можно пренебречь, но она обладает всеми свойствами материального тела(массой).
Сила-величина векторная.
Ее действие на тело определяется:
1)числовым значением или модулем силы
3)точкой приложения силы
Равнодействующая сила-сила равная по модулю сумме (разности) сил, действующих на тело.
Уравновешивающая сила-сила равная по модулю равнодействующей и разная по направлению.
Проекция силы на осьесть алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси.
Аксиомы статики.
1) Аксиома инерции-под действием взаимно уровновешующих сил , материальная точка находится в состоянии покоя или движется прямолинейно и равномерно ( 1 закон Ньютона).
2) Аксиома равновесия 2ух сил-две силы взаимно уровновешующие, только в том случае, если их модули равны и они направлены по одной прямой в разные стороны.
3) Аксиома присоединения или исключения взаимно уровновешующих сил-действия системы сил не изменится, если к ней присоединить или исключить взаимно уравновешивающие силы.
Следствие:не изменяя кинематического состояния твердого тела, силу можно переносить вдоль действия, сохраняя модуль и направление.
Силу можно переносить по линии действия, при этом равновесие тела не изменится, значит сила — скользящий вектор.
4) Аксиома параллелограмма-равнодействующая двух пересекающихся сил построена диагональю, параллелограмм построен на этих силах.
Аксиома равенства действия и противодействия-
6) Аксиома сохранения равновесия сил, приложенных к деформируемому телу при его отвердевании –равновесие сил, приложенных к деформированному телу, сохраняется при его отвердевании(трос, нить, цепь).
Система сходящихся сил. Условия равновесия системы сходящихся сил.
Системой сходящихся силназ. система сил, линии действия которой пересекаются в одной точке.
Условия равновесия системы сходящихся сил.
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая била равна 0, т.е. чтобы силовой многоугольник был замкнут.
Геометрический и аналитический способы сложения сходящихся сил.
Геометрический:1)способ параллелограмма; 2)способ треугольника; 3)способ параллелепипеда; 4)способ силового многоугольника.
Если многоугольник замкнулся, то равнодействующая равна нулю.
Аналитический-этот способ основан на понятии проекции силы на координатную ось.
Дата добавления: 2015-05-05 ; просмотров: 2 | Нарушение авторских прав
Источник
Аналитический способ сложения сил
Проекция равнодействующей сходящейся системы сил на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Пусть на тело действует система сил (F1,…, F4), при этом линии действия сил расположены в плоскости OXY (рис. 1.30).
 |
Их равнодействующая R = F1 + … + F4. Спроецируем составляющие векторы и их равнодействующую на ось OX. Очевидно F1OX > 0, F2OX > 0, F3OX > 0, F4OX 0.
Из рис. 1.30 видно, что ROX = F1OX + F2OX + F3OX + F4OX. Для любой сходящейся системы сил (F1,…, Fn), обозначая их равнодействующую через R, получим:
Зная проекции ROX, ROY, ROZ равнодействующей R на координатные оси, можно найти её модуль и направляющие косинусы.
= 
;
cos(R, i) = ROX/R; cos(R, j) = ROY/R; cos(R, k) = ROZ/R.
Для плоской сходящейся системы сил последние выражения приобретают вид:
= 
;
cos(R, i) = ROX/R; cos(R, j) = ROY/R.
Известно, что сходящаяся система сил уравновешивается только в том случае, если их равнодействующая равна нулю. Графически плоская сходящаяся система сил изображается замкнутым силовым многоугольником (рис. 1.31).
 |
В общем случае
R = Σ Fi = 0.
В замкнутом силовом многоугольнике все силы направлены в одну сторону по обходу многоугольника.
Частный случай. Три сходящиеся силы уравновешиваются, если треугольник этих сил замкнут.
Линии действия трёх непараллельных, взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке (рис. 1.32).
Геометрическое условие равновесия сходящейся системы сил, расположенных в пространстве и на плоскости, одно и то же. Однако графический метод решения задач на равновесие сходящейся системы сил практически применяется только для плоской системы сходящихся сил.
Аналитические условия равновесия
Системы сходящихся сил
В случае если силы взаимно уравновешиваются, их равнодействующая равна нулю. Аналитически это выражается соответствующими уравнениями равновесия.
Для пространственной системысходящихся сил уравнения равновесия имеют вид:
Для плоской сходящейся системы сил уравнения равновесия приводятся к виду:
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей системы отсчёта равнялись нулю.
При помощи этих уравнений можно решить задачи на равновесие сходящейся системы сил на плоскости и в пространстве.
Алгоритм решения задач статики
Как правило, в задачах статики по известным активным силам Fi E требуется определить реакции Ri E внешних связей, наложенных на механическую систему. Напомним, что активные силы и реакции связей относятся к разряду внешних сил. С учётом этого геометрическое условие равновесия внешних сил записывают в следующем виде
Σ Fi E + Σ Ri E = 0.
Для равновесия механической системы необходимо и достаточно, чтобы геометрическая сумма активных сил Fi E и реакций внешних связей Ri E , приложенных к этой системе, равнялась нулю.
При такой системе обозначений внешних сил аналитические условия равновесия пространственной сходящейся системы сил выражаются тремя уравнениями:
Σ 
+ Σ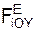 
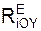
= 0;
Σ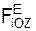 
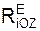
+ Σ 
= 0;
Σ 
+ Σ 
= 0.
Для равновесия механической системы, на которую наложены внешние связи, необходимо и достаточно, чтобы суммы проекций активных сил Fi E и реакций внешних связей Ri E на координатные оси системы отсчёта равнялись нулю.
Для плоской сходящейся системы сил имеем два уравнения:
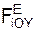
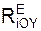
Σ + Σ = 0;
Σ + Σ = 0.
Все задачи на равновесие внешних сил, приложенных к телу, решаются по следующему алгоритму.
Алгоритм решения задач статики
1. Выбирают систему отсчёта.
2. Выбирают тело, к которому приложена система уравновешивающихся сил.
3. Показывают все действующие на тело активные нагрузки.
4. Согласно аксиоме связей действие связей на тело заменяют соответствующими реакциями связей.
5. К полученной системе сил применяют уравнения равновесия, соответствующие этой системе сил.
6. Из уравнений равновесия определяют неизвестные величины.
Источник
Аналитический способ сложения сходящейся системы сил
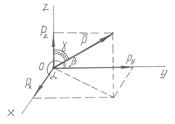
Для аналитического задания силы необходимо выбрать систему координационных осей, по отношению к которым будет определяться направление силы в пространстве.
Вектор, изображающий силу, можно построить, если известны её проекции на прямоугольные декартовы оси координат.
Сила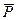 
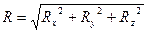
разложена на составляющие 
, которые численно равны проекциям силы на соответствующие оси. Отсюда следует, что если известны проекции силы на оси координат, то можно вектор силы построить геометрически.
,
где 
Чтобы сложить силы аналитически, необходимо вычислить проекции сил на координатные оси.
Аналитическое условие равновесия сходящейся системы сил.
, т.е. и 
, тогда
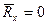
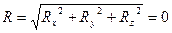
-аналитическое выражение равновесия пространственной сходящейся системы сил.
— для плоской системы сил
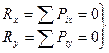
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три взаимноперпендикулярных оси были равны 0.
Лекция 3.
Момент силы относительно точки.
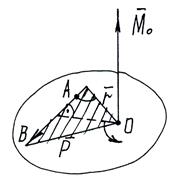
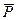
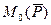
Дано: тело с неподвижной т.О, в т.А приложена сила , которая стремится повернуть тело вокруг т.О. Такое действие силы называется вращательным эффектом. Вращательный эффект изменяется моментом силы относительно точки: 
.
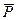
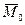
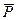
Момент силы относительно т.О изображается вектором 
приложенным в этой точке и направленным перпендикулярно к плоскости, содержащей силу и точку, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу , стремящуюся вращать эту плоскость в сторону, обратную вращению часовой стрелки.
Модуль этого вектора: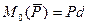 
,
где d – плечо — кратчайшее расстояние от т.О до линии действия силы.
Модуль можно выразить 
Момент силы равен, нулю если d=0
Если в т.А провести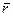 
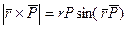
, то 
, но 
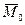
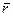
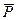
Вектор момента силы относительно т.О можно рассматривать как векторное произведение , проведенного из этой точки в точку приложения силы на вектор силы .
Дата добавления: 2017-02-04 ; просмотров: 468 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
