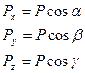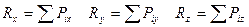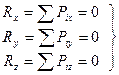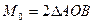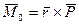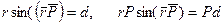Аналитический способ сложения сходящейся системы сил
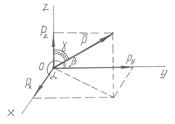
Для аналитического задания силы необходимо выбрать систему координационных осей, по отношению к которым будет определяться направление силы в пространстве.
Вектор, изображающий силу, можно построить, если известны её проекции на прямоугольные декартовы оси координат.
Сила 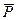


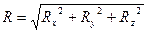
где
Чтобы сложить силы аналитически, необходимо вычислить проекции сил на координатные оси.
Аналитическое условие равновесия сходящейся системы сил.
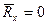
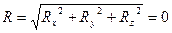
-аналитическое выражение равновесия пространственной сходящейся системы сил.
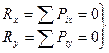
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три взаимноперпендикулярных оси были равны 0.
Лекция 3.
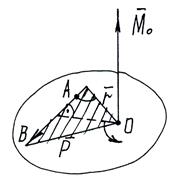
Дано: тело с неподвижной т.О, в т.А приложена сила 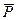
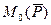
Момент силы 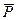
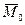
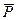
Модуль этого вектора: 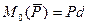
где d – плечо — кратчайшее расстояние от т.О до линии действия силы.
Модуль можно выразить
Момент силы равен, нулю если d=0
Если в т.А провести 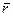
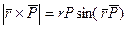
Вектор момента силы 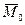
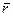
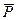
Дата добавления: 2017-02-04 ; просмотров: 466 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Аналитический способ сложения сил
Проекция равнодействующейсходящейся системы сил на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Пусть на тело действует система сил (F1,…, F4), при этом линии действия сил расположены в плоскости OXY (рис. 1.30).
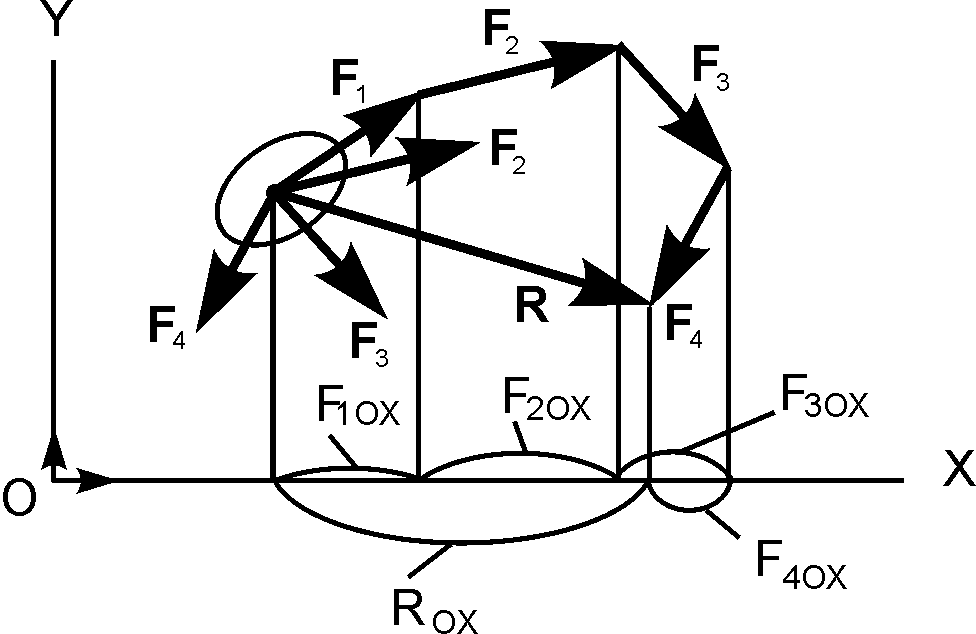 Рис. 1.30 Рис. 1.30 |
Их равнодействующая R = F1 + … + F4. Спроецируем составляющие векторы и их равнодействующую на ось OX. Очевидно F1OX> 0, F2OX> 0, F3OX> 0, F4OX 0.
Из рис. 1.30 видно, что ROX = F1OX + F2OX + F3OX + F4OX. Для любой сходящейся системы сил (F1,…, Fn), обозначая их равнодействующую через R, получим:
Зная проекции ROX, ROY, ROZ равнодействующей R на координатные оси, можно найти её модуль и направляющие косинусы.

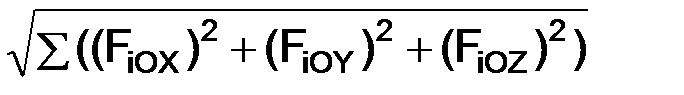
cos(R, i) = ROX/R; cos(R, j) = ROY/R; cos(R, k) = ROZ/R.
Для плоской сходящейся системы сил последние выражения приобретают вид:

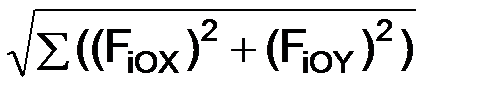
cos(R, i) = ROX/R; cos(R, j) = ROY/R.
Известно, что сходящаяся система сил уравновешивается только в том случае, если их равнодействующая равна нулю. Графически плоская сходящаяся система сил изображается замкнутым силовым многоугольником (рис. 1.31).
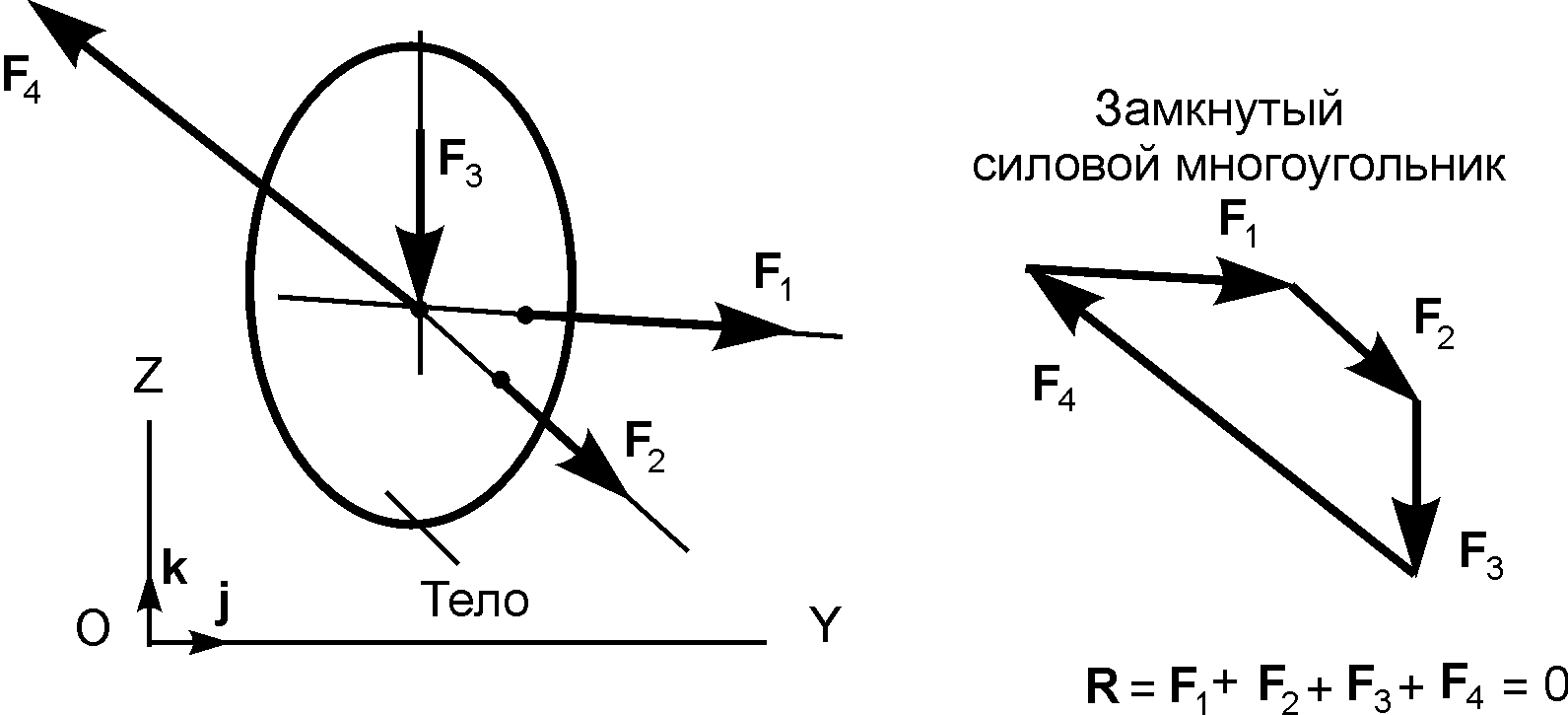 Рис. 1.31 Рис. 1.31 |
В общем случае
R = Σ Fi = 0.
В замкнутом силовом многоугольнике все силы направлены в одну сторону по обходу многоугольника.
Частный случай. Три сходящиеся силы уравновешиваются, если треугольник этих сил замкнут.
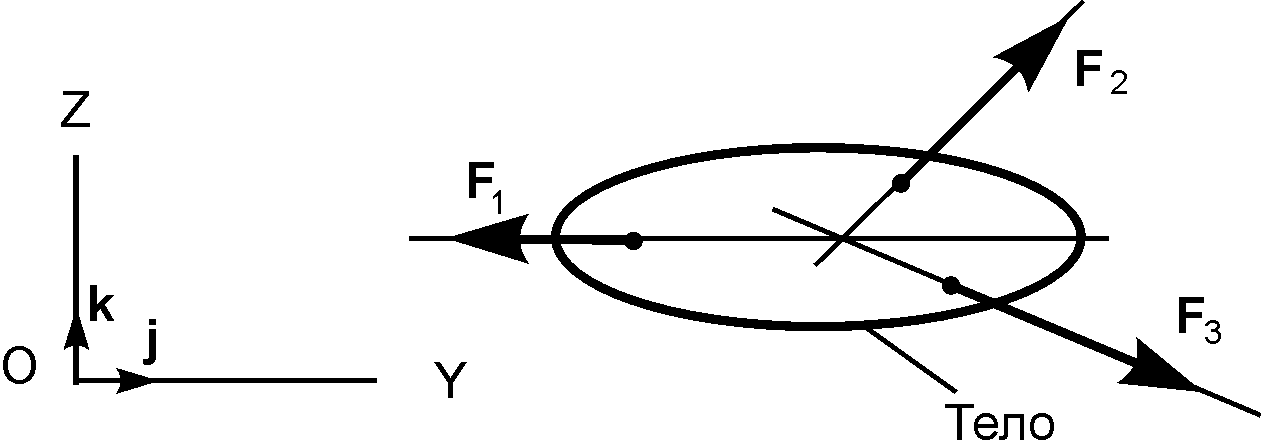 Рис. 1.32 Рис. 1.32 |
Линии действия трёх непараллельных, взаимно уравновешивающихся сил, лежащих в одной плоскости, пересекаются в одной точке (рис. 1.32).
Геометрическое условие равновесия сходящейся системы сил, расположенных в пространстве и на плоскости, одно и то же. Однако графический метод решения задач на равновесие сходящейся системы сил практически применяется только для плоской системы сходящихся сил.
Аналитические условия равновесия
Системы сходящихся сил
В случае если силы взаимно уравновешиваются, их равнодействующая равна нулю. Аналитически это выражается соответствующими уравнениями равновесия.
Для пространственной системысходящихся сил уравнения равновесия имеют вид:
Для плоской сходящейся системы сил уравнения равновесия приводятся к виду:
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из координатных осей системы отсчёта равнялись нулю.
При помощи этих уравнений можно решить задачи на равновесие сходящейся системы сил на плоскости и в пространстве.
Алгоритм решения задач статики
Как правило, в задачах статики по известным активным силамFi E требуется определить реакции Ri E внешних связей, наложенных на механическую систему. Напомним, что активные силы и реакции связей относятся к разряду внешних сил. С учётом этого геометрическое условие равновесия внешних сил записывают в следующем виде
ΣFi E + Σ Ri E = 0.
Для равновесия механической системы необходимо и достаточно, чтобы геометрическая сумма активных сил Fi E и реакций внешних связей Ri E , приложенных к этой системе, равнялась нулю.
При такой системе обозначений внешних сил аналитические условия равновесия пространственной сходящейся системы сил выражаются тремя уравнениями:
Σ 

Σ 

Σ 

Для равновесия механической системы, на которую наложены внешние связи, необходимо и достаточно, чтобы суммы проекций активных сил Fi E и реакций внешних связей Ri E на координатные оси системы отсчёта равнялись нулю.
Для плоской сходящейся системы сил имеем два уравнения:
Σ 

Σ 

Все задачи на равновесие внешних сил, приложенных к телу, решаются по следующему алгоритму.
Дата добавления: 2020-04-25 ; просмотров: 76 ; Мы поможем в написании вашей работы!
Источник
Техническая механика. Конспекты лекций (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Модуль равнодействующей двух сил можно определить из треугольника ACD:
На основании четвертой аксиомы одну силу F∑ можно заменять двумя составляющими силами F1 и F2. Такую замену часто производят при решении задач статики.
Пятая аксиома устанавливает, что в природе не может быть одностороннего действия силы. При взаимодействии тел всякому действию соответствует равное и противоположно направленное противодействие. Так, если на тело В действует сила F1 со стороны материального тела А, то на тело А действует со стороны тела В такая же по численному значению сила F2. Обе силы действуют по одной прямой и направлены в противоположные стороны. Действие и противодействие всегда приложены к различным телам, и именно поэтому они не могут уравновешиваться(рис.6).
Рис.6 Иллюстрации к пятой аксиоме статики
4 Связи и их реакции
Рассматриваемые в механике тела могут быть свободными и несвободными. Свободным называют тело, которое не испытывает никаких препятствий для перемещения в пространстве в любом направлении. Если же тело связано с другими телами, которые ограничивают его движение в одном или нескольких направлениях, то оно является несвободным. Тела, которые ограничивают движение рассматриваемого тела, называют связями.
При взаимодействии между телом и его связями возникают силы, противодействующие возможным движениям тела. Эти силы действуют на тело со стороны связей и называются реакциями связей.
Реакция связи всегда противоположна тому направлению, по которому связь препятствует движению тела. Существование реакций обосновывается аксиомой о действии и противодействии. Для определения реакций связей используют принцип освобождения от связей. Не изменяя равновесия тела, каждую связь можно отбросить, заменив ее реакцией. Определение реакций связей является одной из наиболее важных задач статики. Ниже приведены наиболее распространенные виды связей, встречающиеся в задачах:
1. Связь в виде гладкой (т. е. без трения) плоскости или поверхности. В этом случае реакция связи всегда направлена по нормали к опорной поверхности (рис.7а).
2. Связь в виде контакта цилиндрической или шаровой поверхности с плоскостью. В этом случае реакция связи направлена также по нормали к опорной поверхности (рис.7б).
3. Cвязь в виде шероховатой плоскости. Здесь возникают две составляющие реакции: нормальная Rn, перпендикулярная плоскости, и касательная Rt, лежащая в плоскости. Касательная реакция Rt называется силой трения и всегда направлена в сторону, противоположную действительному или возможному движению тела.
Полная реакция R, равная геометрической сумме нормальной и касательной составляющих R=Rn+Rt, отклоняется от нормали к опорной поверхности на некоторый угол р. При взаимодействии тела с реальными связями возникают силы трения. Однако во многих случаях силы трения незначительны и вследствие этого ими часто пренебрегают (рис.7в).
4. Гибкая связь, осуществляемая веревкой, тросом, цепью и т. п. (рис.7г). Реакции гибких связей направлены вдоль связей, причем гибкая связь может работать только на растяжение.
5. Связь в виде жесткого прямого стержня с шарнирным закреплением концов. Здесь реакции всегда направлены вдоль осей стержней. Стержни при этом могут быть как растянутыми, так и сжатыми (рис.7д).
6. Связь, осуществляемая ребром двугранного угла или точечной опорой. Реакция такой связи направлена перпендикулярно поверхности опирающегося тела (рис.7е).
Рис.7 Виды связей.
Тема 1.2 Плоская система сходящихся сил
Лекция № 3 «Плоская система сходящихся сил»
1. Плоская система сходящихся сил
Рис. 8 Силовой многоугольник
Рассмотрим равновесие системы сходящихся сил. Сходящимися называются силы, линии действия которых пересекаются в одной точке (рис. 8а). Существуют два способа сложения пересекающихся сил: геометрический (рис. 8б) и аналитический (рис. 8в).
Геометрический способ сложения сходящихся сил.
От произвольной точки О откладываем вектор, равный силе 




Аналитический метод сложения сходящихся сил. Проектируя векторное равенство 



Flx + F2x + F3x = Rx;
F1 cos 



Отсюда определим значение равнодействующей всех сходящихся сил:
и направление вектора 
Условием равновесия системы сходящихся сил является равенство нулю модуля равнодействующей 
Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из осей координат была равна нулю.
Метод проекций
Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.
Рис.9 Виды проекций
Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (—), если направление от начала проекции к ее концу противоположно положительному направлению оси.
Тема 1.3 Пара сил и момент силы относительно точки
Лекция № 4 «Пара сил. Момент силы»
Парой сил называют две силы 

Сила, действующая на тело, может не только смещать его, но и поворачивать вокруг какой-нибудь точки. Пусть сила 
Моментом силы F относительно некоторого центра О называется величина, равная произведению силы на кратчайшее расстояние от точки О до линии действия силы и взятая с соответствующим знаком. Знак «плюс» соответствует моменту силы, которая стремится повернуть тело вокруг точки О против хода часовой стрелки, а знак «минус» — если сила стремится повернуть тело по направлению движения часовой стрелки. Если линия действия силы проходит через точку, то момент силы относительно этой точки равен нулю. Перпендикуляр, опущенный из точки О на линию действия силы 
Источник