Аналитический способ решения квадратных неравенств 8 класс

Понятие о квадратном неравенстве и его решении, аналитический способ решения — КВАДРАТНОЕ НЕРАВЕНСТВО И ЕГО РЕШЕНИЕ — КВАДРАТНЫЕ НЕРАВЕНСТВА

Цель: рассмотрение квадратного неравенства и его решения, аналитического способа решения.

I. Сообщение темы и цели урока

II. Изучение нового материала (основные понятия)

Понятие квадратного неравенства аналогично понятию квадратного уравнения. Если в одной части неравенства стоит квадратный трехчлен, а в другой — число нуль, такое неравенство называют квадратным. Например, неравенства 3х2 — 2х — 1 ≤ 0 и -5х2 + 3х + 2 > 0 являются квадратными. Вообще, если в части неравенства переменная х входит в степени 2 и ниже, то после несложных преобразований такое неравенство сводится к квадратному.

В неравенстве 2х2 ≥ 5х — 3 перенесем (изменяя знак) члены 5х и -3 в левую часть и получим квадратное неравенство 2х2 — 5х + 3 ≥ 0.

Напомним, что решением неравенства с одним неизвестным называется такое значение неизвестного, при котором это неравенство обращается в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет. Например, для неравенства примера 1 число х = 2 является одним из решений, а число х = 1,2 — нет.

К квадратным неравенствам приводят многие геометрические и текстовые задачи.

Одну сторону квадрата увеличили на 2 см, а другую — на 6 см. Площадь получившегося прямоугольника стала больше 45 см3. Какова была сторона квадрата?

Пусть сторона квадрата равна х см, тогда стороны прямоугольника (х + 2) см и (х + 6) см и его площадь равна (х + 2)(х + 6) см2. По условию задачи получаем неравенство (х + 2)(x + 6) > 45 или х2 + 8х + 12 > 45, или x2 + 8x – 33 > 0. Разложим левую часть неравенства на множители (х – 3)(х + 11) > 0. Так как по условию х > 0, то и х + 11 > 0. Разделим обе части неравенства на положительное выражение х + 11, (при этом знак неравенства сохраняется) и получаем линейное неравенство х — 3 > 0, откуда х > 3. Итак, сторона квадрата больше 3 см.

На плану производит построение рота солдат, состоящая не менее чем из 72 человек. Оказалось, что шеренг на 6 больше, чем солдат в каждой шеренге. Сколько может быть солдат в каждой шеренге?

Пусть число солдат в каждой шеренге равно х, тогда число шеренг равно х + 6 и число солдат в роте равно х(х + 6). По условию задачи получаем неравенство х(х + 6) ≥ 72 или х2 + 6х – 72 ≥ 0. Разложим левую часть этого квадратного неравенства на множители (х + 12)(х — 6) ≥ 0. Так как по условию х > 0, то и х + 12 > 0. Разделим обе части неравенства на положительное выражение х + 12 (при этом знак неравенства сохраняется) и получаем линейное неравенство х — 6 ≥ 0, откуда х ≥ 6. Итак, в каждой шеренге находится не менее 6 солдат.

Заметим, что в двух последних примерах по условию задачи возникало дополнительное условие х > 0, что позволило легко свести квадратное неравенство к линейному неравенству и решить его. Теперь рассмотрим решение квадратных неравенств (без ограничений на х).

Решим неравенство x2 + 8х – 33 > 0.

Квадратное уравнение х2 + 8х — 33 = 0 имеет два корня x1 = -11 и х2 = 3. Поэтому квадратный трехчлен x2 + 8x — 33 можно разложить на множители x2 + 8x – 33 = (x + 11)(x — 3). Тогда данное неравенство имеет вид (х + 11)(х — 3) > 0. Произведение двух множителей положительно, если они имеют одинаковые знаки. Рассмотрим два случая.

1) Пусть оба множителя положительны, т. е. х + 11 > 0 и х — 3 > 0. Получаем систему линейных неравенств Решая систему, имеем откуда х > 3. Итак, все числа х > 3 являются решениями неравенства (х + 11)(x — 3) > 0.

2) Пусть оба множителя отрицательны, т. е. х + 11 0. Таким образом, решениями неравенства (х + 11)(x — 3) > 0, а следовательно, и данного неравенства х2 + 8х – 33 > 0 являются числа х 3. Итак, х 3.

Итак, при решении квадратного неравенства ax2 + bx + c > 0 или ax2 + bx + c 0 или а(х – х1)(x – х2) 0). Итак, при a = 2 решение данного неравенства х = 2.

3) Пусть a > 2. Тогда получаем две системы линейных неравенств: или (решение этой системы 2 ≤ х ≤ a) и или (такая система решений не имеет, т. к. а > 2). Итак, при а > 2 решение данного неравенства 2 ≤ х ≤ а.

Так как в задачах с параметрами очень важен правильный ответ, то выпишем ответ данной задачи: при а 2 2 ≤ х ≤ а.

Заметим, что аналогичный подход можно использовать и при решении неравенств с модулями. При этом надо помнить, что при возведении в квадрат неотрицательных частей неравенства знак неравенства сохраняется и получается равносильное неравенство (т. е. имеющее те же решения, что и данное неравенство). Учитывая свойство модуля |а| = а2, отпадает необходимость раскрытия модуля.

Решим неравенство

Возведем в квадрат обе неотрицательные части данного неравенства и получим: или (при этом знак модуля исчезает). Перенесем все члены неравенства в левую часть Используя формулу разности квадратов, разложим эту часть на множители. Имеем: или или Произведение множителей положительно, если множители х — 2 и х + 1 имеют одинаковые знаки. Получаем две системы линейных неравенств.

1) или Решение этой системы х > 2.

2) или Решение этой системы х 2.

Решим неравенство

Возведем в квадрат обе неотрицательные части данного неравенства и получим: или (при этом знаки модулей исчезают). Перенесем все члены неравенства в левую часть Используя формулу разности квадратов, разложим эту часть на множители. Имеем: или или Произведение множителей отрицательно, если множители 2 — х и 3х — 1 имеют разные знаки. Получаем две системы линейных неравенств.

1) или Решение этой системы x 2.

Итак, решение данного неравенства х 2.

III. Контрольные вопросы

1. Какое неравенство называется квадратным? Приведите примеры.

2. Что называется решением неравенства с одной переменной?

3. Что значит решить неравенство?

4. Как решают квадратное неравенство (опишите алгоритм)?

IV. Задание на уроке

№ 649; 650 (1, 4); 651 (1, 2); 652 (2, 3); 653 (1, 4); 654 (5); 655 (1, 4); 657.

V. Задание на дом

№ 650 (2, 3); 651 (3, 4); 652 (1,4); 653 (2, 3); 654 (6); 655 (2, 3); 658.

VI. Творческие задания

1. При всех значениях параметра а решите неравенство:

Ответы: а) при всех а х = a/2;

б) при всех а х — любое число, кроме х = -3/4а;

в) при всех а решений нет;

г) при всех а х — любое число;

д) при а 1, при а = 1 х — любое число, кроме х = 1, при а > 1 х a;

е) при а 1 2 ≤ х ≤ 2а;

ж) при а 3 3 -4 х ≤ -4 и х ≥ a;

и) при a > 0 х ≤ 2а и х ≥ a, при a = 0 х — любое число, при a > 0 х ≤ a и х ≥ 2a.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.

Источник

Решение квадратных неравенств. Цель изучения: формирование понятия квадратного неравенства и обучение аналитическому способу решения квадратного неравенства. — презентация

Презентация была опубликована 8 лет назад пользователемАнна Юрина

Похожие презентации

Презентация на тему: » Решение квадратных неравенств. Цель изучения: формирование понятия квадратного неравенства и обучение аналитическому способу решения квадратного неравенства.» — Транскрипт:

1 Решение квадратных неравенств

2 Цель изучения: формирование понятия квадратного неравенства и обучение аналитическому способу решения квадратного неравенства в случае положительного дискриминанта трёхчлена, стоящего в левой части.

3 1 Является ли каждое из чисел 0; 1; 5; -2 решением неравенства 2х-1

4 3 Зная, что х- отрицательное число, сравнить с нулём значение выражения: 1) х-2 2) — х 3) -2х — 1

5 4 К обеим частям неравенства х

6 5 Обе части неравенства х

0 3) ½ x +1 > 0 2) – х 0 3) ½ x +1 > 0 2) – х 7 6 Решить неравенство : 1) х+5 > 0 3) ½ x +1 > 0 2) – х 0 3) ½ x +1 > 0 2) – х 0 3) ½ x +1 > 0 2) – х 0 3) ½ x +1 > 0 2) – х 0 3) ½ x +1 > 0 2) – х

2 x>5 3) x 5 x» title=»7 Решить систему неравенств : 1) x>2 x>5 3) x 5 x» > 8 7 Решить систему неравенств : 1) x>2 x>5 3) x 5 x 2 x>5 3) x 5 x»> 2 x>5 3) x 5 x»> 2 x>5 3) x 5 x» title=»7 Решить систему неравенств : 1) x>2 x>5 3) x 5 x»>

0 или 0; х²-4 0″ title=»Неравенство вида ах²+bх + с> 0 или 0; х²-4 0″ > 9 Неравенство вида ах²+bх + с> 0 или 0; х²-4 0 0 или 0; х²-4 0″> 0 или 0; х²-4 0″> 0 или 0; х²-4 0″ title=»Неравенство вида ах²+bх + с> 0 или 0; х²-4 0″>

10 Если в левой части неравенства стоит квадратный трёхчлен, а в правой части- 0, то такое неравенство называют квадратным. Решить неравенство с одним неизвестным- найти то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство. Решить неравенство-это значит найти все его решения или установить, что их нет.

0 х-2>0 или x-20 x-32 x3 x» title=»1)x²-5x+6=0 х =2 или х = 3 x²- 5х +6= (х -2)(х-3) (х-2)(х-3)>0 х-2>0 или x-20 x-32 x3 x» > 11 1)x²-5x+6=0 х =2 или х = 3 x²- 5х +6= (х -2)(х-3) (х-2)(х-3)>0 х-2>0 или x-20 x-32 x3 x 0 х-2>0 или x-20 x-32 x3 x»> 0 х-2>0 или x-20 x-32 x3 x»> 0 х-2>0 или x-20 x-32 x3 x» title=»1)x²-5x+6=0 х =2 или х = 3 x²- 5х +6= (х -2)(х-3) (х-2)(х-3)>0 х-2>0 или x-20 x-32 x3 x»>

12 23 23 Ответ: (- ; 2) U (3 ; + )

13 В классе:649, 650, 651. Задача 2, 3 из п Дома: п.40, 652(2,4).

14 Квадратные неравенства Решение квадратного неравенства с помощью системы из двух неравенств Составила: Шутова Е. Г.

Источник

Квадратные неравенства, примеры, решения

В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.

Что представляет собой квадратное неравенство

Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.

Квадратное неравенство – это такое неравенство, которое имеет вид a · x 2 + b · x + c 0 , где a , b и c – некоторые числа, причем a не равно нулю. x – это переменная, а на месте знака может стоять любой другой знак неравенства.

Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y = a · x 2 + b · x + c .

Приведем пример квадратного неравенства:

Возьмем 5 · x 2 − 3 · x + 1 > 0 . В этом случае a = 5 , b = − 3 и c = 1 .

Или вот такое неравенство:

− 2 , 2 · z 2 − 0 , 5 · z − 11 ≤ 0 , где a = − 2 , 2 , b = − 0 , 5 и c = − 11 .

Покажем несколько примеров квадратных неравенств:

Здесь коэффициенты этого квадратного неравенства есть ; 1 2 3 · x 2 — x + 5 7 0 , в этом случае a = 1 2 3 , b = — 1 , c = 5 7 .

Особое внимание нужно обратить на тот факт, что коэффициент при x 2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b · x + c > 0 , так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.

Пример такого неравенства x 2 − 5 ≥ 0 .

Способы решения квадратных неравенств

Основным метода три:

• графический;
• метод интервалов;
• через выделение квадрата двучлена в левой части.

Графический метод

Метод предполагает проведение построения и анализа графика квадратичной функции y = a · x 2 + b · x + c для квадратных неравенств a · x 2 + b · x + c 0 ( ≤ , > , ≥ ) . Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.

Метод интервалов

Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a · x 2 + b · x + c при их наличии.

Для неравенства a · x 2 + b · x + c 0 решениями являются промежутки со знаком минус, для неравенства a · x 2 + b · x + c > 0 , промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.

Выделение квадрата двучлена

Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида ( x − p ) 2 q ( ≤ , > , ≥ ) , где p и q – некоторые числа.

Неравенства, сводящиеся к квадратным

К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.

Приведем пример. Рассмотрим равносильное преобразование неравенства 5 ≤ 2 · x − 3 · x 2 . Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3 · x 2 − 2 · x + 5 ≤ 0 .

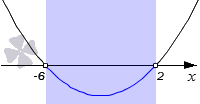
Необходимо найти множество решений неравенства 3 · ( x − 1 ) · ( x + 1 ) ( x − 2 ) 2 + x 2 + 5 .

Решение

Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:

3 · ( x − 1 ) · ( x + 1 ) − ( x − 2 ) 2 − x 2 − 5 0 , 3 · ( x 2 − 1 ) − ( x 2 − 4 · x + 4 ) − x 2 − 5 0 , 3 · x 2 − 3 − x 2 + 4 · x − 4 − x 2 − 5 0 , x 2 + 4 · x − 12 0 .

Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.

D ’ = 2 2 − 1 · ( − 12 ) = 16 , x 1 = − 6 , x 2 = 2

Построив график, мы можем увидеть, что множеством решений является интервал ( − 6 , 2 ) .

Ответ: ( − 6 , 2 ) .

Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2 · x 2 + 5 x 2 + 6 · x + 14

равносильно квадратному неравенству x 2 − 6 · x − 9 0 , а логарифмическое неравенство log 3 ( x 2 + x + 7 ) ≥ 2 – неравенству x 2 + x − 2 ≥ 0 .

Источник