Аналитический способ разбора задач
На основе аналитического и синтетического методов решения задач при работе над поиском решения задачи применяются два основных способа разбора задачи: аналитический (анализ) и синтетический (синтез). Однако на практике чаще употребляют аналитическо-синтетический разбор задачи.
Под анализом подразумевают способ рассуждений от общего к частному (анализировать – разбивать на составляющие), таким образом при разборе текста задачи от вопроса к данным применяется аналитический способ.
Под синтезом подразумевают способ рассуждений от частного к общему (синтезировать – получать из частей). В задачах это разбор от данных к вопросу, однако, назвать этот метод чисто синтетическим нельзя, т.к. прежде, чем получать метод разбора от данных к вопросу, эти данные нужно предварительно вычленить из задачи, т.е. проанализировать условие задачи.
Непосредственно сам разбор задачи представляет собой цепочку рассуждений, основанных на анализе и синтезе. Организуя разбор задачи вместе с детьми, учитель должен продумать систему специально подобранных вопросов, при помощи которых организуется выбор решения задачи. Эти вопросы не должны быть наводящими, должны вести к самостоятельному выбору решения. Разбор составной задачи заканчивается составлением плана решения. Если вы разбираете задачу с одновременным составлением схемы разбора, то план решения прослеживается прямо по схеме.
Проиллюстрируем различные способы разбора задач на примере следующей задачи: «За день туристы преодолели 100 км. 84 км они проехали автобусом, а остальной путь прошли пешком за 4 часа. Сколько километров туристы проходили за 1 час?» [Б3, №716].
В результате анализа содержания задачи появляется ее краткая запись в виде чертежа:
Направление рассуждений будет следующим:
1) Разбор от вопроса к данным.
Что спрашивается в задаче? (Сколько км туристы проходили за 1 час?) Что нужно знать, чтобы ответить на этот вопрос? (Путь, который прошли туристы и время, которое они затратили на этот путь). Можно ли сразу узнать, сколько км туристы проходили за 1 час? (Нельзя, т.к. мы не знаем путь, который они прошли). Можно ли сразу узнать путь, пройденный пешком? (Можно). Почему вы думаете, что можно? (Так как мы знаем общий путь и путь, пройденный пешком). Далее осуществляется наметка плана решения.
Источник
Аналитический метод решения



При аналитическом методе решения отправляются не от условия задачи, как это делают при синтетическом методе, а от ее требования, вопроса. Это характерно для всех разновидностей аналитического метода, применяемых при решении задач.
Решение задач аналитическим методом начинается с постановки следующего вопроса, связанного с требованием решаемой задачи: «Что нужно знать, чтобы ответить на вопрос данной задачи (выполнить требование)?» Для правильного ответа на поставленный вопрос необходимо знать данные задачи и учитывать те зависимости, которые связывают их с искомым числом.
Пусть для вычисления искомого Y основной задачи требуется знать, например, числа p1 и q1, из которых при помощи некоторого математического действия можно получить Y, т.е. решить основную задачу. Итак, основная задача с требованием Y преобразовалась в первую серию вспомогательных задач с искомыми p1 и q1. Обозначим первую серию вспомогательных задач через В1. Ставим тот же вопрос к каждой из вспомогательных задач: «Что нужно знать, чтобы найти p1 (q1)?» и опять при ответе на этот вопрос используем условие А основной задачи, а также арсенал математической теории.
Пусть для вычисления p1 нужно знать p2 и q2, а для вычисления q1 – знать 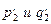
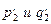
Продолжая процесс преобразования, получаем, наконец, такую серию (Вn) вспомогательных задач, искомые которых содержатся во множестве данных основной задачи.
Итак основная задача решена аналитическим методом, поскольку этим методом проведен поиск и найден путь решения задачи; главное здесь именно в этом, а не в оформлении записи уже известного решения.
Найденное аналитическое решение можно изложить различными способами, в том числе и синтетическим. В последнем случае пришлось бы следовать от конца аналитического рассуждения к его началу, не производя при этом никаких поисков.
Если основную задачу условно записать формулой А 

Где А 



К рассмотренной в предыдущем пункте текстовой задаче применим аналитический метод решения. Наличие двух искомых в задаче несколько осложняет построение рассуждений, поэтому можно ограничиться сначала одним искомым, найти его и затем воспользоваться им как уже известным числом при отыскании пути получения второго искомого. Рассмотрим схему:
- За сколько часов может выполнить всю работу, работая отдельно, та машина, которая продолжила работу?
- Часть всей работы, выполненная этой машиной.
- Сколько часов работала эта машина отдельно когда она работала отдельно
- Объем всей работы
- Часть всей работы, выполненная двумя машинами совместно
- За сколько часов машины вместе Выполнят всю работу?
- Сколько часов они работали совместно?
Такой поиск обычно проводится устно и завершается составлением плана решения. Аналогично теперь можно построить схему аналитического поиска второго числа основной задачи (сделайте самостоятельно!).
В практике решения задач методы анализа и синтеза полностью разделить, изолировать друг от друга невозможно. Они полезно сочетаются. При аналитическом методе имеют место скрытые элементы синтеза. Например, преобразуя требование основной задачи в требования первой серии вспомогательных задач, мы неявно проверяем правильность этого преобразования, возможность синтезирования из искомых чисел задач первой серии искомого основной задачи.
Широкое применение находит аналитический метод при решении геометрических задач на вычисление. Здесь удобно начинать решение с соответствующей формулы, которая и показывает, какой будет первая серия вспомогательных задач и т.д. Кратко продемонстрируем это на примере следующей геометрической задачи.
Задача. В конус вписана пирамида, основанием которой служит прямоугольный треугольник и боковая грань которой, проходящая через один из катетов основания, образует с плоскостью основания двугранный угол α. Найти объем пирамиды, если образующая конуса равна l и наклонена к плоскости основания под углом β.

Р е ш е н и е. Начертим конус с вписанной в него пирамидой МАВС, в которой длины боковых ребер МА = МВ = МС = l, АС – гипотенуза треугольника АВС, центр основания конуса – точка О, Ао = ОС, ÐМАО=β, ÐМDО = α.
Формула объема пирамиды 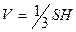
Из прямоугольного треугольника ОМА находим Н = ОМ = lsinβ.
Для нахождения площади основания надо найти длины катетов АВ и ВС. (Получаем вторую серию из двух вспомогательных задач.)
Для определения АВ достаточно найти ОD – длину средней линии треугольника АВС, а для вычисления ВС надо найти АС ( третья серия из двух вспомогательных задач; решение первой задачи уже известно):
OD = MO ctgα = l sinβ ctg α.
Для получения АС достаточно знать АО ( четвертая серия – одна задача, которую можно решить):
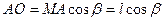
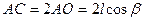
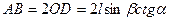
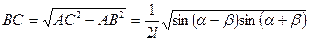
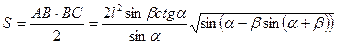
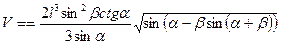
Приведенное решение является очень кратким (отсутствуют выкладки, обоснования), чтобы выделить метод решения. Учащиеся, чтобы научиться решать задачи, должны делать полные математические выкладки и уметь обосновывать каждый свой шаг в процессе решения ссылкой на условие задачи или изученную математическую теорию.
Хотя путь поиска на основе аналитического метода решения не всегда однозначен, однако он все же менее многозначен и более определен, чем путь поиска при синтетическом методе решения. Аналитический метод удобен для поиска пути решения новой для учащихся задачи, он опирается на определенное умение школьника рассуждать и эффективно способствует развитию его продуктивного, логического и функционального мышления. В результате систематического применения аналитического метода решения задач у учащихся быстрее формируется умение cамостоятельно решать новые для них задачи, чем при пользовании синтетическим методом.
Источник
Аналитический подход в решении математических задач.
статья на тему
В статье описаны основные этапы решения текстовых задач в курсе математики 5 — 6 классов.
Скачать:
| Вложение | Размер |
|---|---|
| analiticheskiy_podhod_v_reshenii_matematicheskih_zadach.docx | 19.25 КБ |
Предварительный просмотр:
Камалутдинова Светлана Михайловна,
учитель математики МОУ СОШ с углублённым изучением отдельных предметов № 1 города Малмыжа.
Аналитический подход в решении математических задач
Умение решать задачи – один из основных показателей математического развития ученика, глубины усвоения им учебного материала. Любой экзамен, любая проверка знаний содержит в качестве основной и, пожалуй, наиболее важной части, решение задач.
Как показывает моя практика подготовки к итоговой аттестации, многие учащиеся даже не приступают к решению задач, пропуская их.
Психологические исследования данной проблемы показывают, что причина несформированности умений и способностей в решении задач состоит в том, что школьники не получают необходимых знаний о сущности задач и их решений и поэтому решают задачи, не осознавая свою деятельность. Ребята не стараются понять, в чём состоят приёмы и методы решения задач, стараются как можно быстрее решить задачу, решают их лишь ради получения ответа, не вникая в процесс решения.
Значит для того, чтобы научить детей решать задачи, надо научить их разбираться в том, что они собой представляют, как устроены, из каких частей состоят, каковы инструменты, с помощью которых производится их решение.
И если мы сумеем научить школьников не просто получать правильный ответ при решении задач, а анализировать задачу, проникать в её сущность, обучим приёмам поиска решений, различным методам решения, то в дальнейшем они не будут испытывать трудностей при решении не только математических, но и любых, в том числе жизненных задач.
Особое внимание уделяю обучению решению текстовых задач. Ещё в начальной школе дети обучаются решению таких задач, поэтому перед тем как взять 5 класс, я консультируюсь с учителем об умениях каждого ученика решать текстовые задачи, изучаю методику работы учителя над задачей, посещаю уроки математики.
В 5 классе обращаю внимание на работу с каждым этапом решения текстовых задач. Выделяют следующие этапы решения задачи:
- Анализ содержания задачи;
- Схематическая запись;
- Поиск способа решения задачи;
- Осуществление решения задачи;
- Проверка решения задачи;
- Исследование задачи;
- Формулировка ответа задачи;
- Анализ решения задачи;
При этом все 8 этапов можно не выделять, достаточно рассмотреть 5 основных этапов (подчёркнуты). Но я при работе с задачей уделяю существенное внимание и схематической записи, так как считаю это существенным звеном при решении задач.
Этап анализа содержания задачи, на мой взгляд, является одним из наиболее важных этапов решения задачи. Основная цель на данном этапе : выявить все имеющиеся связи между данными и искомыми величинами. Очень важно на данном этапе понять содержание задачи. При этом помогают вопросы:
- О чём говорится в задаче?
- Каков тип задачи?
- Информация о решении такой задачи.
- Все ли понятия и термины вам знакомы?
- Каким числом может выражаться ответ задачи?
Данная работа должна быть постоянной для того, чтобы ребёнок, при самостоятельном решении текстовых задач, автоматически отвечал на эти вопросы.
Результаты предварительного анализа нужно фиксировать. Я учу это делать на втором этапе решения задач в виде схематической записи. Использую разные виды схематической записи:
Считаю, что удачно выполненная схематическая запись условия – это залог успешного решения задачи. Кроме того, схематическая запись даёт возможность ликвидировать у большей части учащихся страх перед текстовой задачей и правильно выбрать способ решения.
Цель этапа поиска решения задачи: выбрать метод решения задачи и составить план решения. Вопросы, помогающие составить план решения задачи:
- Решали ли вы аналогичную задачу? Если такая задача была решена, то план составить не трудно.
- Известна ли вам задача, к которой можно свести решаемую? Чтобы ответить на этот вопрос, часто приходится прибегать к совету: переформулировать условие задачи.
Если же ученики затрудняются ответить на эти вопросы, то приходится искать другие способы решения. Многие ученики решение задачи начинают с вопроса: Что мы можем найти, исходя из имеющихся данных? При решении арифметических задач это не создаёт больших проблем, но в дальнейшем приводит к избыточному решению геометрических задач. Поэтому я приучаю своих учеников решать задачи, начиная с вопроса, по следующему алгоритму:
- Что нужно найти в задаче?
- Какие величины для этого нужно знать?
- Знаем ли мы эти величины?
- Можем ли мы найти неизвестные величины?
- Что для этого нужно сделать?
Анализ задачи по данному алгоритму мы проводим как в виде таблицы, так и виде схемы.
Большое внимание при решении задач уделяю поиску разных способов решения задачи, по возможности стараюсь разобрать все способы, предложенные учениками. Это помогает каждому ученику выбрать оптимальный путь решения задачи.
Кроме арифметического и алгебраического способов решения текстовых задач знакомлю ребят с ещё одним методом – методом перебора. Знание этого метода поможет ребятам со слабой математической подготовкой, особенно при решении текстовых задач ГИА. Кроме того, данный метод находит применение и при решении более сложных задач.
Как правило, у учеников большие затруднения возникают при решении задач на смеси, сплавы, растворы. Знание разных способов решения таких задач помогает выбрать оптимальный способ для каждого ученика. В основном мы решаем такие задачи алгебраическим способом. Я знакомлю своих ребят и с арифметическим способом решения (Представлен в презентации).
Учить осмысленному подходу к решению текстовых задач мне помогает учебник математики под редакцией Г. В. Дорофеева, в котором выделены такие типы задач, как задачи на части и задачи на уравнивание. В 7 классе умение решать такие задачи позволяет более осмысленно подходить к решению уравнений и позволяет решать геометрические задачи арифметическим способом. Также в этом учебнике рассматриваются задачи на совместную работу, даётся алгоритм решения таких задач.
Такая системная, целенаправленная работа над текстовыми задачами приводит к тому, что ученики приучаются анализировать любое математическое задание и более осмысленно подходить к его выполнению, что пригодится ребятам при выполнении заданий ГИА и ЕГЭ.
Источник









