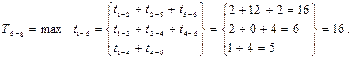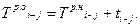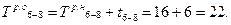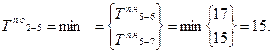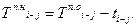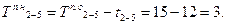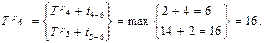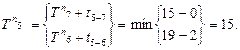Аналитический способ расчета сетевых графиков

Аналитический способ расчета сетевых графиков

«Организация, планирование и управление строительным производством» под общей редакцией профессора И.Г.Галкина, Москва, «Высшая школа», 1978г. стр. 89-121

Сетевая модель календарного плана

Недостатки линейных календарных планов в значительной мере устраняются при использовании сетевых моделей, позволяющих не только рассчитать основные параметры графика, определяющие продолжительность выполнения программы в целом и сроки начала и окончания взаимосвязанных работ в составе комплекса, но и анализировать график, выявлять резервы и использовать их для его улучшения (оптимизации).

Сетевая модель календарного плана является наиболее удачной для отражения вероятностных производственных процессов. Она позволяет в более наглядной форме отобразить порядок возведения сложного объекта.

В строительной практике построение сетевого графика преимущественно ведется по типу «работы-дуги», поскольку при большом числе входящих и выходящих работ для одного события такой тип построения графика оказывается наиболее удобным.

При таком построении работа в сетевом графике изображается сплошной стрелкой, причем в зависимости от характера графика и степени его детализации одной стрелкой может быть изображен комплекс работ, либо отдельная операция. На рис. 1 сплошными стрелками (дугами) показаны работы — предшествующая, данная работа и последующая. Стрелки в сетевом графике не имеют масштаба и определенного угла наклона, однако все они должны иметь направление, ведущее от начала к завершению программы, т. е. слева направо.

У начала программы стоит исходное событие, не имеющее непосредственно предшествующих событий. Событие у начала любой работы называют начальным или предшествующим, а у конца работы — конечным или последующим.

К каждому событию может непосредственно примыкать несколько предшествующих (входящих) работ и несколько последующих (выходящих) работ, Событие в этом случае отражает совокупность условий, позволяющих начать одну или несколько работ лишь при окончании некоторых других (непосредственно предшествующих) работ.

В конце программы стоит завершающее событие, не имеющее непосредственно следующих работ.
Для точного обозначения предшествования одной работы другим работам в необходимых случаях вводятся дополнительные дуги (в виде пунктирных стрелочек), выполняющие функции связей (или фиктивных работ) (рис. 2 ).

Для удобства кодирования и анализа сети не допускают, чтобы несколько параллельно выполняемых работ имели общие начальные или общие конечные события. На рис. 3 показан фрагмент такого графика с вводом дополнительных связей. Между исходным и завершающим событием лежит несколько технологически связанных между собой цепочек работ, выполняемых последовательно. Поскольку к некоторым событиям примыкают «входящие» и «выходящие» работы, выполняемые параллельно, цепочки последовательно выполняемых работ как бы пересекаются, образуя сеть с узлами в местах событий.

Как указывалось выше, событие фиксирует состояние, а не является процессом, требующим затрат времени или труда. Все события нумеруются от исходного до завершающего.

Сетевые модели могут быть одноцелевые и многоцелевые.

Одноцелевой сетевой моделью называют сетевой график, который составлен для достижения единственной цели. Завершающее событие в такой графике является целевым событием.

Многоцелевые сети предусматривают достижение нескольких целей, в том числе промежуточных.

Для оперативного контроля к управления строительством при планировании в сетевом графике могут быть выделены контрольные события, привязанные к календарным датам. Каждая работа характеризуется продолжительностью ее выполнения, получаемой в результате подсчета объема работ, трудоемкости, выбора метода ее выполнения, средств механизации и состава рабочей бригады.

В комплексе работ, отраженном на сетевом графике, имеются работы, выполняемые последовательно и параллельно. При рассмотрении какой-либо работы в сети различают непосредственно предшествующую ей работу и последующую.

При наличии данных о продолжительности выполнения каждой работы в сетевом графике представляется возможным проследить все цепочки последовательно выполняемых работ от исходного события до завершающего и определить общую продолжительность каждой цепочки. Самый продолжительный по времени путь от исходного до завершающего события называют критическим. Им определяется продолжительность выполнения всей программы работ.

Критический путь обозначается на графике двойными или жирными стрелками. Близкие к критическому по продолжительности пути называют подкритическими. Все другие, менее продолжительные пути называют некритическими и работы, лежащие на этих путях,— некритическими. Не исключено, что в одном графике может быть два и даже несколько критических (равных по продолжительности) путей.

В зависимости от размера сетевого графика (числа работ и событий) количество критических работ, т. е. лежащих на критическом пути, обычно бывает не более 10-15% от общего числа работ, что позволяет руководителям строительства сосредоточивать внимание прежде всего на этих работах, от которых зависит соблюдение установленного общего срока строительства.

Сетевые модели бывают детерминированные и вероятностные. В последних учитываются некоторые неопределенные данные о параметрах, составе и порядке выполнения работ.

Простейшая одноцелевая модель с учетом времени (ПДВ—простейшая детерминированная временная) должна в качестве исходной информации иметь единственное исходное событие i0 и единственное завершающее событие.

Продолжительность каждой работы в сети, т. е. временная1 опенка дуги (стрелки) обозначается t_i-j.

В качестве исходной информации задается начало выполнения комплекса работ, а в некоторых случаях — директивная продолжительность строительства или срок ввода в действие объекта.

На основе расчета модели определяется критическое время T_кр, т. е. минимальное время, в течение которого может быть осуществлена программа. Остальные параметры сетевого графика имеют следующие обозначения:

t_h-i — продолжительность предшествующей работы;
t_i-j — продолжительность данной работы, у которой предшествующее событие i, а последующее j;
t_j-k — продолжительность последующей работы;
t рн _i-j— раннее начало работы;
t ро _i-j — раннее окончание работы;
t пн _i-j — позднее начало работы;
t по _i-j — позднее окончание работы;
R_i-j— полный запас времени работы;
r_i-j—частный запас времени работы.

Источник

Расчет сетевого графика аналитическим путем

Расчет временных параметров СГ может выполняться по работам или по событиям.

Расчет по работам. Раннее начало работы T р.н _i—j – самое раннее из возможных время начала работы.

Например, для работы 6-8 (рис. 5.5) раннее начало

Так как продолжительность наибольшего пути 1-2, 2-5, 5-6 составляет 16, то работу 6-8 можно начать на 17 день.

T р.о _i—j – раннее окончание работы – начата в самый ранний из возможных сроков

Например, для работы 6-8 раннее окончание

T п.о _i—j – позднее окончание работы i – j – самый поздний из допустимых сроков окончания работы, при котором не увеличивается общая продолжительность работ сетевого графика:

Определение позднего начала через позднее окончание основано на том, что расчет ведут от завершающего события, у которого ранние и поздние сроки совпадают, т.е. T р _k= T п _k, поэтому, рассчитав ранние сроки работ, мы установили тем самым и поздний срок завершающего события:

Для работы 2-5 позднее окончание

T п.н _i—j – позднее начало работы – самый поздний из допустимых сроков начала работы, при котором не увеличивается общая продолжительность работ. T п.н _i—j равно разности между величинами ее позднего окончания и продолжительности:

Для работы 2-5 позднее начало

Расчет по событиям. T р _i – ранний срок свершения события i определяют максимальной величиной суммы ранних сроков свершения предшествующих событий и продолжительности работ, входящих в данное событие:

Например,

T п _i – поздний срок свершения события j определяется минимальной величиной из значений разности поздних сроков свершения конечных событий k и продолжительности работ, выходящих из данного события j.

Например, для события 5

Для критических работ соблюдаются следующие условия:

1. ранние и поздние сроки начала работы и соответственно их окончания равны, т.е.

или при расчете по событиям ранние и поздние сроки свершения событий, ограничивающих данную работу, соответственно равны, т. е.

2. разность между возможными сроками окончания и начала работы равна ее продолжительности, т.е.

или разность между сроками свершения конечного и начального событий равна продолжительности данной работы, т.е.

Например, для критической работы 3-7 первое условие T р.н _3-7 = T п.н _3-7 = 10; T р.о _3-7 = T п.о _3-7 = 15 соблюдено. Второе условие также выполняется: T о _3-7 — T н _3-7 = t_3-7; 15-10=5.

Общий (полный) и частный резервы времени для работ критического пути равны нулю.

R . _i—j – общий (полный) резерв времени работы i–j – это максимальное время, за которое можно задержать начало работы или увеличить ее продолжительность без изменения общего срока строительства. Определяется разностью поздних и ранних сроков начала или окончания работы:

Например, общий резерв времени для работы 4-6 составляет

или то же самое по событиям:

r . _i—j – частный (свободный) резерв времени работы i–j – максимальное количество времени, на которое можно перенести начало работы или увеличить ее продолжительность без изменения раннего начала последующих работ. Оно имеет место, когда в событие входят 2 работы или больше, и определяется разностью значений раннего начала последующей работы и раннего окончания данной работы.

Источник

Разработка сетевого графика проекта

Процесс расчета параметров сетевого графика

Сетевой график проекта располагает операции в подходящей последовательности для расчета времени начала и окончания операции . Оценка продолжительности операции проводится на основе затрат времени, требуемого для решения всех задач, составляющих набор работ операции .

С помощью нескольких простых расчетов можно выполнить прямой и обратный анализ сетевого графика проекта. Этот анализ даст ответы на следующие вопросы:

Прямой анализ — Определение ранних сроков начала операций

1. Как скоро может начаться операция? (ранний старт — ES )
2. Как скоро она может закончиться? (ранний финиш- EF )
3. Как скоро может быть завершен проект в целом? (предполагаемое время- ТЕ )

Обратный анализ — Определение поздних сроков завершения операций

1. Каковы самые поздние сроки начала операции? (позднее начало — LS )
2. Каковы самые поздние сроки завершения операции? (позднее окончание — LF )
3. Какие операции составляют критический путь ( СР )? Это самый длинный путь , при задержке выполнения операций на этом пути задерживается выполнение проекта.
4. На какое время может быть задержано выполнение операции? (резерв времени — SL )

Термины в скобках являются общепринятыми обозначениями и используются в большинстве книг по управлению проектами

Прямой анализ — определение ранних сроков начала операций

Процесс прямого анализа разворачивается от первых операций проекта, проходя по всем цепочкам последовательных операций сетевого графика до самой последней операции проекта.

По мере продвижения по любому из путей производится добавление времени выполнения операций. Самый длинный путь показывает время завершения проекта в целом и называется критическим путем ( СР ).

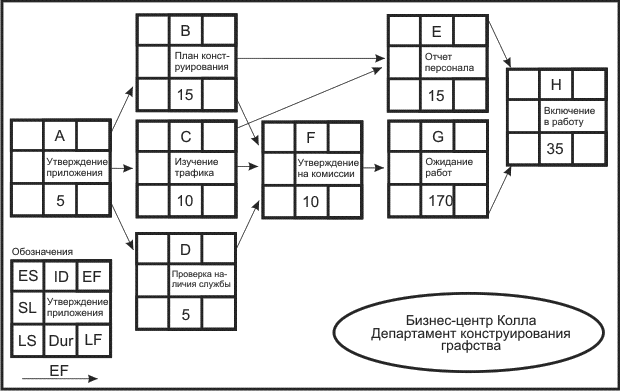
В табл. 2.2 представлено время операций в рабочих днях для проекта бизнес-центра Колла.

На рис. 2.5 показана система с оценкой продолжительности операций, которую вы можете видеть в блоке.

Например, операция А имеет продолжительность 5 дней, операция G -170 рабочих дней.

Поступательный путь начинается со времени начала проекта, которое обычно принимается равным нулю.

Таблица 2.2. Информация для сетевого графика

Бизнес-центр Колла
Операция	Описание	Предшествующая операция	Время операции
А	Утверждение приложения	нет	5
В	Планы конструирования	А	15
С	Изучение трафика	А	10
D	Проверка наличия службы	А	5
Е	Отчет персонала	В , С	15
F	Одобрение комиссии	В , C , D	10
G	Ожидание работ	F	170
Н	Включение в работу	Е , G	35

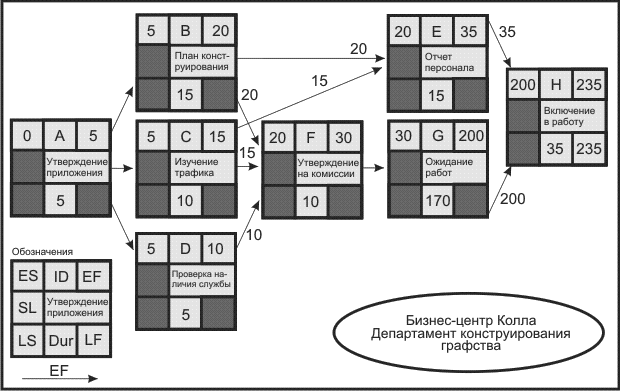
В нашем примере, ранний срок начала первой операции (операция- А ) это 0. Это время проставляется в верхнем левом углу блока операции А (рис. 2.6).

Самое раннее окончание операции А это 5 ( ES + Dur или 0 + 5 = 5 ).

Далее мы видим, что операция А предшествует операциям B , C , D .

Следовательно, самое раннее время начала этих операций — это момент завершения операции А , 5 рабочих дней.

На рис. 2.6 можно видеть, что операции В , С и D могут начаться в момент завершения операции А , и поэтому все они имеют раннее начало ( ES ) 5.

Используя формулу ES + Dur = EF , раннее время завершения этих операций — В , C , D -( EF ) будет, соответственно, 20 , 15 , и 10 .

Какое же тогда будет раннее время начала ( ES ) для операции Е, которая является операцией слияния?

Это будет 15 или 20 ? Ответ — 20 , так как все операции, непосредственно предшествующие операции Е ( В и С ) должны быть завершены до начала операции Е . Поскольку для завершения операции В требуется более продолжительное время, она и определяет раннее начало ( ES ) операции Е .

Тот же процесс используется для определения ES для операции F . Ей предшествуют операции В , C , и D . Операция В является определяющей для времени раннего окончания ( EF ), которой требуется больше времени ( 20 против 15 и 10 ), чем операциям ( В , C , и D ), непосредственно предшествующим операции F .

Прямой анализ предполагает, что каждая операция начинается в тот момент, когда завершается последняя предшествующая ей операция. При расчете времени раннего начала операций в процессе прямого анализа необходимо помнить три вещи:

1. Вы добавляете время операции на каждом шаге анализа ( ES + Dur = EF )
2. Вы переносите раннее завершение ( EF ) предшествующей операции до следующей, у которой оно же становится временем раннего начала ( ES ), если только
3. Последующая операция не является операцией слияния.В этом случае вы выбираете самое большое по значению время раннего окончания ( ЕF ) среди всех непосредственно предшествующих операций.

В нашем примере на рис. 2.6 ЕF для операции F (30) проводится до операции G , где становится ее ES (30).

Мы видим, что операция Н является операцией слияния и, следовательно, необходимо найти самое большое по значению EF у непосредственно предшествующих ей операций ( Е и G ). В этом случае выбор происходит между временем EF 35 и 200 ; выбор ES операции Н 200 EF для операции Н ( 235 ) становится самым ранним расчетным временем ( ТЕ ), когда проект может быть завершен в целом.

Таким образом, на все три вопроса, которые ставятся в процессе прямого анализа, были получены ответы.

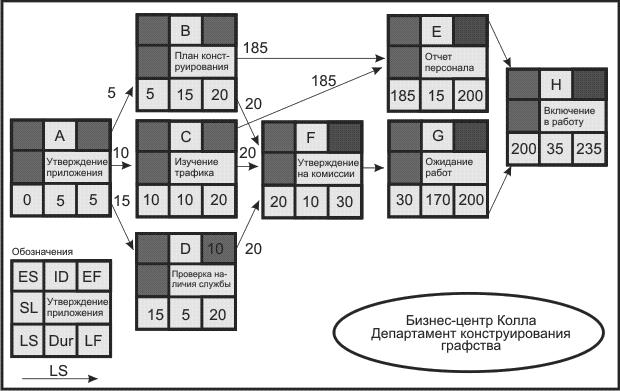
Обратный анализ — определение поздних сроков завершения операций

Обратный анализ начинается с самой последней операции сетевого графика .

Каждый раз, выполняя шаг назад к началу сетевого графика , необходимо вычитать время рассматриваемой операции из общей продолжительности проекта в целом, с тем, чтобы определить сроки ее самого позднего возможного начала ( LS ) и окончания ( LF ) выполнения. За исходную временную точку при выполнении обратного анализа выбирается время позднего окончания самой последней операции проекта. В этой операции данное время совпадает с временем раннего окончания ее выполнения ( EF ) (или в случае нескольких завершающих операций, операции с самым большим ( EF )). В некоторых случаях имеются установленные крайние сроки продолжительности проекта, тогда будут использоваться именно эти сроки. Предположим, что мы можем принять EF предполагаемого окончания проекта ( ТЕ ) равным 235 рабочим дням. LF для операции Н становится 235 рабочих дней ( EF

Обратный анализ похож на прямой. Выполняя его, следует помнить три вещи:

1. Вы вычитаете время операции на каждом шаге, начиная с последней операции проекта ( LF — Dur = LS ).
2. Вы переносите LS на предшествующую операцию и приравниваете ей LF к ней, если
3. Предшествующая операция не является операцией дробления; в противном случае вы выбираете наименьший LS из всех операций, которым данная операция дает начало, и приравниваете к этому значению ее LF .

Давайте применим эти правила к нашему примеру с бизнес-центром Колла. Начинаем с операции Н (включение в работу) и ее LF в 235 рабочих дней, LS для операции Н оказывается равным 200 рабочих дней ( LF — Dur = LS или 235 — 35 = 200 ).

LS для операции Н становится LF для операций Е и G . LS для операций Е и G становится соответственно 185 ( 200 — 15 = 185 ) и 30 рабочих дней ( 200 — 170 = 30 ).

LS для операции G становится LF для операции F , и ее LS становится 20 .

Здесь мы видим, что операции В и C являются операциями дробления, которые связаны с операциями Е и F . Поздний финиш для операции В контролируется LS операций Е и F . LS для операции Е — 185 дней и для операции F — 20 дней. Идите по стрелке назад от операций Е и F к операции В .

Отметим, что время LS для операций Е и F помещено в правый блок, и вы можете выбрать наименьшее время — 20 дней.

Заключительная операция В может быть завершена за 20 дней; в противном случае выполнение операции F задержится, задержится и выполнение проекта.

LF для операции C идентично операции В , поскольку она также определяет LS операций Е и F .

Операция D просто получает свое позднее окончание ( LF ) от операции F .

Вычислив LS ( LF — Dur = LS ) для операций В , C , D , мы можем определить LF для операции А , которая является операцией дробления.

Окончание операции А определяется операцией В , которая является наименьшим LS для операций В , С и D .

Так как LS для операции В составляет период времени 5 , LF для операции А — 5 , и ее LS — период времени — 0 .

Обратный анализ завершен, и сроки последней операции известны.

Источник