Аналитический способ построения модели

Способы построения моделей

В зависимости от характера и объема априорной информации выделяют два способа построения моделей объектов и систем управления:

Аналитический способ применяется для построения моделей объектов хорошо изученной природы. В этом случае имеется вся необходимая информация, но она представлена в иной форме. Реализуемые при этом модели представляются в виде схем с сосредоточенными параметрами (компонентами). На таких моделях базируются, например, теоретическая механика и теоретическая электротехника.

Методы теории управления абстрагируются от конкретной природы объектов и оперируют более абстрактными – математическими (символьными) моделями.

Аналитический способ моделирования состоит из двух основных этапов:

− построения схемы объекта;

− построение математического описания схемы в требуемой форме.

При этом принципиальные проблемы моделирования решаются на первом (неформальном) этапе, а второй является процедурой преобразования форм представления моделей. Это позволяет разработать и использовать различные компьютерные программы автоматизации составления уравнений по схемам.

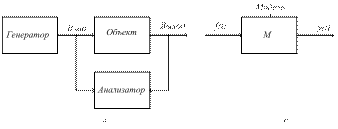
Экспериментальный способ применяется, когда свойства объекта изучены в недостаточной степени либо слишком сложны для аналитического описания. Он заключается в активных экспериментах над объектом или пассивной регистрации его поведения в режиме нормальной эксплуатации (рис. 1.19, а).

Рис. 1.19. Экспериментальное исследование (а) и модель «вход-выход» (б)

В результате обработки данных наблюдений получают модели в требуемой форме. Совокупность этих операций носит название «идентификация объекта». В результате идентификации получают модели «вход-выход» (рис. 1.19, б). Очевидно, что получаемая модель зависит не только от свойств объекта, но и от разнообразия входных сигналов.

Поскольку объект на практике не является «черным ящиком», т.е. о нем что-то известно, то есть возможность комбинировать оба способа: вначале аналитически строить структуру модели и определять приближенные значения параметров, а затем обработкой экспериментальных данных уточнять эти значения.

Используются три основных класса структур моделей систем управления:

– с причинно-следственной структурой;

Модели «вход-выход» отображают зависимость поведения системы от входных воздействий при целостном представлении системы (в виде «черного ящика»). Внутренние переменные (переменные состояния) в них выражаются через входные и выходные переменные.

При построении модели системы с раскрытой причинно-следственной структурой объект или систему предварительно расчленяют на элементы направленного действия и рассматривают их как преобразователи сигналов. Элементы выделяются по функциональному признаку: объект управления, измерительные, преобразовательные и усилительные элементы, устройство управления, исполнительный механизм и т.д. Для каждой части строится своя модель, соединением которых, в соответствии с соединением элементов образуется модель системы. Принципиальной трудностью является создание таких моделей систем с контурами: не зная свойств частей, нельзя знать сигналы на входах этих частей, а без этого нельзя идентифицировать сами части.

В иерархическом представлении структурные модели систем представляются уровнями иерархии (интеграции). При этом модели «вход-выход» являются моделями нулевого уровня причинно-следственной интеграции. Разделение модели «вход-выход»на подсистемы приводит к первому уровню причинно-следственной интеграции и т.д. Дальнейшее раскрытие структур подсистем, каждая из которых снова рассматривается как модель «вход-выход», приводит к многоуровневым (иерархическим) моделям. Часто иерархический подход является единственно возможным для проектирования сложных систем. При этом предполагается, что поведение подсистемы L-го уровня полностью объясняется свойствами подсистем непосредственно нижележащего L-1-го уровня.

Модели среды. Среда на входе системы моделируется автономными системами двух типов:

− генераторами типовых воздействий;

− преобразователями типовых воздействий (фильтрами).

В качестве типовых воздействий используются единичные импульсная и ступенчатая функции, «белый шум». Часто используются также случайные входные воздействия. Некоторые из этих воздействий будут рассмотрены далее.

Детальному исследованию перечисленных типов моделей должно предшествовать рассмотрение математического аппарата, применяемого при исследовании моделей. Поэтому рассмотрим математические средства, применяемые при описании систем управления.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Основы аналитических методов построения математических моделей

Классификация математических моделей.

Роль математического моделирования при исследовании, проектировании и эксплуатации теплотехнических систем.

При разработке и исследовании техн-их объектов важным фактом явл-ся технико-экономическое обоснования, в котором рассм-ся предполагаемые источники финансирования. В рез-те этого обоснования проводят выбор рациональных структур и оптимальных пар-ров теплотехнических сис-м. Устное решение этих задач на современном уровне не возможно без применения матем. модели. Реализация матем. модели на данном этапе существующего объекта позволяет решать задачи:

1.исследовать хар-р взаимосвязи и пар-ров сис-мы и проанализировать их влияние на основные показатели, как технические, так и экономические.

2.исследовать влияние внешних условий сооружения и эксплуатации теплоэнергетической установки на соотношение ее пар-ров и технико-экономических показателей.

3.численно оценить дополнительные материальные вложения, снижения КПД, изменения приведенных затрат и ряда других показателей сис-мы, в случае отказа оптимальных пар-ров и схем из-за каких-нибудь технических или экономических причин.

4.оценить структурную и параметрическую оптимизацию сис-мы.

Матем. моделирование позволяет выполнять в едином интерактивном пр-се расчет технологической схемы установки и технические расчеты оборудования, при этом достигается значение тепловых балансов, теплового гидравлического и прочностного эл-ов оборудования, определение тепловых и гидравлических потерь, уточнение КПД и основных показателей сис-мы установок. Такое взаимное уточнение без применения методов мат. моделирования невозможно в виду сложности и трудоемкости многократного повторения расчетов. При этом следует помнить, что мат. модели, разработанные на стадии проектирования технического объекта, м.б. использованы на этапе его эксплуатации. В виду физ. старения оборудования происходит изменение его технических пар-ров, а 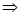изменяются: значения оптимальных пар-ров, которые должны уточняться периодически или постоянно при эксплуатации оборудования. При выполнении технико-экономического обоснования следует учитывать, что теплоэнергетические сис-мы явл-ся эл-ми топливно-энергетического комплекса страны, а так же они взаимосвязаны с другими пром. отраслями, а именно металлургией и машиностроением. Вследствие этого при оптимизации следует учитывать не только внутренние связи, но и внешние, т.е. необходимо учитывать общее состояние развития, энергетики, металлургии, машиностроения, вопросы взаимодействия с о.с. Учет внешних связей еще более усложняет задачу оптимизации. В то же время применения матем. моделирования позволяет не только описать известные связи хар-щие исследуемый объект, но так же позволяет раскрыть новые закономерности, как в самом объекте, так и при его взаимодействии с внешними сис-ми. Следует так же учитывать, что применение матем. моделирования повышает ответственность исполнителями, т.е. чел-ка, участвующего в пр-се проектирования оборудования, т.к. возрастает производительность его труда, а и выполняемые объемы за одно и то же время. Таким образом, при выполнении технико-экономического обоснования с применением метода мат. моделирования, необходимо иметь обобщенную модель, включающую в себя модель структуры сис-мы матем. модели эл-ов сис-мы, мат. модели с взаимодействиями с внешней сис-ой. В то же время следует отметить, что основной сложностью внедрения мат. моделирования в инженерную практику, явл-ся большие затраты труда на создание мат. моделей, и создания программного обеспечения для реализации мат. моделей.

Сущ-ет ряд классификаций мат. моделей по различным признакам. Отметим некоторые из них. По признаку соотношений для больших технических сис-м мат. модели можно разделить на 2 группы:

1.детерминированные, т.е. модели, в которых состояние сис-мы в заданный момент времени однозначно определяется через значения ее пар-ров, входящую инф-цию и начальные условия.

2.вероятностные (стохастические), т.е. модели по средствам, которых можно определить лишь распределение вероятностей для состояния сис-мы при известных ее пар-рах, входной ее инф-ции и начальных условий.

В зависимости от способа использования мат. модели при ее реализации можно выделить аналитические модели, когда пр-сы функционирования записываются в виде некоторых функциональных соотношений и логических условий и имитационные модели, когда создается спец. алгоритм, при реализации которого воспроизводится функционирование объектов во времени. Мат. модель можно исследовать 3 способами: аналитически, когда при построении модели в ее основу закладывается некоторая явная зависимость в общем виде; численно, когда невозможно получить аналитическую зависимость, но можно получить численное решение, описывающее состояние сис-мы; качественно, когда возможно только определить некоторые св-ва предполагаемого решения.

, , , , — имея эту зависимость, мы можем рассчитать т-ру в любой точке, либо время.

. Чтобы решить более точно, необходимо применять аналитические методы решения. Мы разбиваем печь на n –частей, делаем интегральный расчет. От уровня представления сис-мы матем. модели м.б. разделены на: модели микроуровня – это уровень теплофизических пр-сов, протекающих в эл-ах теплоэнергетических установок; макроуровень – это уровень теплотехнических установок и сис-м; метод уровня – это уровень взаимодействия теплотехнических сис-м с внешними сис-ми.

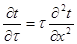
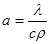
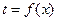
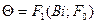
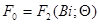
Методы построения мат. моделей можно разделить на 3 вида: аналитический, имперический и комбинированный.

По способу их построения: ручные и автоматизированные.

Аналитические методы построения мат. модели позволяют получить мат. описание объекта исследования в широком диапазоне изменения его пар-ров. Сам пр-сс построения модели в данном случае включает в себя следующие этапы:

1. теоретический анализ пр-сов, протекающих в объекте исследования.
2. определение пр-сов наиболее существенно влияющих на работу объекта, в зависимости от поставленной задачи исследования.
3. определение пар-ров, хар-щих каждый из пр-сов, выбранных на 2-м этапе: описание статики и динамики этих пр-сов.
4. построение мат. модели для объекта в целом, исходя из описания выделенных пр-сов.

В данном способе получения мат. модели наиболее трудно подается алгоритмизация, и в каждом случае требуется индивидуальный подход т.е. не сущ-ет универсального алгоритма, позволяющего построить модель аналитическим способом. Тем не менее сущ-ют общие основные подходы:

1-я общая черта закл-ся в том, что в основу построения мат. модели, закладываются основ- ные законы природы, а именно законы сохранения материи и движения, которые дополня-ются при необходимости законами, полученными опытным путем. Законы сохранения записывают в виде закона сохранения в-ва (материального баланса), и закона сохранения движения или энергии (энергетический баланс). Эти у-ния представляются на диф. уровне по принципу “прибыль” – “убыль” = 0 – для статических или стационарных; и “прибыль” – “убыль” = “приращение” – для нестационарных или динамических. В рез-те применения аналитических методов к пр-сам гидроаэродинамики и ТМО, получают мат. описание в виде у-ния или сис-мы у-ний, (диф. частных производных), которые дополняют- ся условиями однозначности, в которые входят: геометрические пар-ры исследуемой сис-мы, граничные условия и начальные условия. Совокупность граничных и начальных условий наз-ют краевыми условиями.

2-я общей чертойаналитического метода построения мат. модели явл-ся институт допущений. В виду нашей ограниченности знаний об исследуемой сис-ме и невозможности построения абсолютно точной модели необходимо вводить ряд допущений. В качестве примера перечислим допущения, которые применяются при изучении теплопроводности в твердых телах:

1. тело однородно и изотропно.

2. физ. пар-ры постоянны.

3. деформация рассм-мого объема, связанное с изменением т-ры, явл-ся очень малой величиной по сравнению с самим объемом.

4. макроскопические частицы тела неподвижны относительно друг друга.

5. внутренние источники теплоты в теле, которые в общем случае м.б. заданны как ф-ции от координат, распределены равномерно.

При применении аналитических методов построения мат. модели часто необходимо включать дополнительное у-ние, или численные пар-ры, полученные опытным путем, или в рез-те физ. эксперимента, что вызвано необходимостью сделать сис-му у-ний замкнутой или другими словами привести к соответствию число у-ний к числу неизвестных пар-ров.

Источник