Построение графика функции методом дифференциального исчисления
Правила ввода функции
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Пример №1 . Провести полное исследование функции 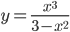
1) Функция определена всюду, кроме точек 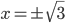
2) Функция нечетная, так как f(-x) = -f(x) , и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.
3) Функция не периодическая.
4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.
5) Функция имеет разрыв второго рода в точке 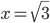
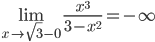
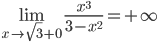
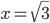
6) Находим 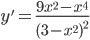
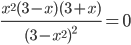
В окрестности точки x3=3 имеет: y’>0 при x 3, следовательно, в точке x3 функция имеет максимум, ymax(3)=-9/2. Найти первую производную функции
7) Находим 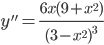

8) Выясним вопрос об асимптотах.
Наличие вертикальной асимптоты 

Найдем наклонные асимптоты: 

9) Теперь, используя полученные данные, строим чертеж:

Пример №2 . Построить график функции 
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем 

4. Точки разрыва x=0 , причем 
Найдем наклонные асимптоты: 

Наклонная асимптота имеет уравнение y=x .
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем 
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.
Источник
Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины
Понятие модуля является одной из важнейших характеристик числа в области действительных чисел, широко применяется в различных разделах школьного курса математики, физики, но рассмотрение задач, связанных с понятием модуля ( а тем более исследование и построение графиков функций, содержащих знак модуля ) появляется лишь эпизодически, в рамках изучения той или иной темы. Тем не менее, задачи, связанные с модулями построением графиков функций, содержащих знак модуля, часто встречаются на математических олимпиадах, вступительных экзаменах в ВУЗы, ЕГЭ.
Цель моей исследовательской работы: изучить соответствующие теоретические материалы, выявить алгоритм построения графиков функции, аналитическое выражение которых содержит знак абсолютной величины.
Объект исследования: линейные функции, квадратичные и кубические функции, аналитическое выражение которых содержит знак абсолютной величины.
В результате исследования графиков функции, аналитическое выражение которых содержит знак абсолютной величины, я получала возможность знать и понимать определение модуля действительного числа, правила построения графиков функций, содержащих знак модуля; уметь применять определение, свойства модуля к решению конкретных задач, читать и строить графики функций, содержащих знак модуля, графически решать уравнения и неравенства, применять компьютерную программу для исследования и построения графиков функций, содержащих знак модуля.
При выполнении исследовательской работы я сформировала алгоритмы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины. Это функции: у=f |(х)|, у=|f(х)|, у=|f |(х)| |.
Скачать:
| Вложение | Размер |
|---|---|
| muhamatdinova_.doc | 124.5 КБ |
| muhamatdinova_dinara_.ppt | 2.48 МБ |
Предварительный просмотр:
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИИ, АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ КОТОРЫХ СОДЕРЖИТ ЗНАК АБСОЛЮТНОЙ ВЕЛИЧИНЫ
Мухаматдинова Динара Рамзиевна,
МОУДОД Центр внешкольной работы Агрызского муниципального района РТ, Кучуковская СОШ
ученик 10 класса.
Бурганиева А.Р., учитель математики высшей категории Кучуковской СОШ Агрызского муниципального района РТ
2. Геометрическая интерпретация понятия |а |—————————- — -5
Цель и задачи работы: изучить соответствующие теоретические материалы, выявить алгоритм построения графиков функции, аналитическое выражение которых содержит знак абсолютной величины.
Объект исследования : функции, содержащие знак абсолютной величины.
Предмет исследования: закономерность графиков функции у = f |(х)|,
у = | f (х)|, у = | f |(х)| |.
Методы исследования : решение примеров на построения графиков, сравнение, анализ, обобщение.
Построение графиков функций одна из интереснейших тем в школьной математике. Один из крупнейших математиков нашего времени Израиль Моисеевич Гельфанд писал: «Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это – построение графиков – является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Например, если написано y=x 2 , то Вы сразу видите параболу; если y=x 2 -4, Вы видите параболу, опущенную на четыре единицы; если же y=4-x 2 , то Вы видите предыдущую параболу, перевернутую вниз. Такое умение видеть сразу и формулу, и ее геометрическую интерпретацию – является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с Вами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».
Хотя уравнения с модулями мы начали изучать уже с 6-го – 7-го класса, где мы проходили самые азы уравнений с модулями. Я выбрал именно эту тему, потому что считаю, что она требует более глубокого и досконального исследования. Я хочу получить более широкие знания о модуле числа, различных способах построения графиков, содержащих знак абсолютной величины.
Цель работы: изучить соответствующие теоретические материалы, выявить алгоритм построения графиков функции, аналитическое выражение которых содержит знак абсолютной величины.
Объект исследования: линейные функции, квадратичные и кубические функции, аналитическое выражение которых содержит знак абсолютной величины.
Методы исследования: решение примеров на построения графиков, сравнение, анализ, обобщение.
II. Основная часть.
1. Историческая справка.
В первой половине XVII века начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма(1601-1665) и Рене Декарт (1596-1650) представляли себе функцию как зависимость ординаты точки кривой от её абсциссы. А английский ученый Исаак Ньютон(1643-1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки.
Термин «функция» (от латинского function – исполнение , совершение) впервые ввел немецкий математик Готфрид Лейбниц(1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли(1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер(1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п.
Модуль объемного сжатия( в физике)- отношение нормального напряжения в материале к относительному удлинению.
Определение. Модуль числа a или абсолютная величина числа a равна a , если a больше или равно нулю и равна -a , если a меньше нуля:
Из определения следует, что для любого действительного числа a,
2. Геометрическая интерпретация понятия модуля |а |
Каждому действительному числу можно поставить в соответствие точку числовой прямой, это точка будет геометрическим изображением данного действительного числа. Каждой точке числовой прямой соответствует её расстояние от начало отсчета, или длина отрезка, начало которого в точке начала отсчета, а конец – в данной точке. Длина отрезка всегда рассматривается как величина неотрицательная. Геометрической интерпретацией действительного числа служит вектор, выходящий из начала отсчета и имеющий конец в точке, изображающей данное число. Длина этого вектора будет геометрической интерпретацией модуля данного действительного числа.
3. График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f (х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f (х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
1. Построить график функции у= |х|
- Если х≥0, то |х| =х и наша функция у=х, т.е. искомый график совпадает с биссектрисой первого координатного угла.
- Если х
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
Из сопоставления двух графиков: у=х и у= |х|, я сделаю вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Из сопоставления двух графиков: у = х и у = -х, я выдвинула гипотезу, что график функции у = f(|х|) получается из графика у = f (x) при х ≥0
симметричным отображением относительно оси ОУ.
Можно ли применять этот метод построения графиков для любой функции, содержащей абсолютную величину? Для этого я рассмотрела несколько функций, и сделала для себя выводы.
1. Построить график функции у=0,5 х² — 2|х| — 2,5
1) Поскольку |х| = х при х≥0, требуемый график совпадает с параболой у=0,5 х² — 2х — 2,5 . Если х у=0,5 х² + 2х — 2,5 .
2) Если рассмотрим график у=0,5 х² -2х — 2,5 при х≥0 и отобразить его относительно
оси ОУ мы получим тот же самый график.
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину? Для этого я рассмотрела несколько функций, и сделала для себя вывод.
2. Например: у=х 2 — |х| -3
1) Поскольку |х| = х при х≥0, требуемый график совпадает с параболой у=0,25 х² — х — 3. Если х у=0,25 х² + х — 3.
2) Если рассмотрим график у=0,25 х² — х — 3 при х≥0 и отобразить его относительно оси ОУ мы получим тот же самый график.
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
х 2 -4х -12 = 0 Имеем, х 1 = — 2; х 2 = 6.
(-2; 0) и (6; 0) – координаты точки пересечения графика функции с осью ОХ.
Значит, часть требуемого графика, соответствующая значениям х 0.
б) Поэтому достраиваю для х
Докажем, что график функции у = f |(х)| совпадает с графиком функции у = f (х) на множестве неотрицательных значений аргумента и симметричен ему относительно оси ОУ на множестве отрицательных значений аргумента.
Доказательство: Если х≥0, то f |(х)|= f (х), т.е. на множестве неотрицательных значений аргумента графики функции у = f (х) и у = f |(х)| совпадают. Так как у = f |(х)| — чётная функция, то её график симметричен относительно ОУ.
Таким образом, график функции у = f |(х)| можно получить из графика функции
у = f (х) следующим образом:
1. построить график функции у = f(х) для х>0;
Вывод: Для построения графика функции у = f |(х)|
1. построить график функции у = f(х) для х>0;
2. Для х отразить построенную часть
относительно оси ОУ.
4. График функции у = | f (х)|
Построить график функции у = |х² — 2х|
Освободимся от знака модуля по определению
Если х² — 2х≥0, т.е. если х≤0 и х≥2, то |х² — 2х|= х² — 2х
Я вижу, что на множестве х≤0 и х≥2 графики функции
у = х² — 2х и у = |х² — 2х|совпадают, а на множестве (0;2)
графики функции у = -х² + 2х и у = |х² — 2х|совпадают. Построю их.
График функции у = | f (х)| состоит из части графика функции у = f(х) при у ≥0 и симметрично отражённой части у = f(х) при у
- Построить график функции у = |х² — х — 6 |
1) Если х² — х -6≥0, т.е. если х≤-2 и х≥3, то |х² — х -6|= х² — х -6.
2) Построим у = х² — х -6 . Нижнюю часть графика
симметрично отбражаем относительно ОХ.
Сравнивая 1) и 2), видим что графики одинаковые.
Докажем, что график функции у = | f (х)| совпадает с графиком функции у = f (х) для f(х) >0 и симметрично отражённой частью у = f(х) при у
Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у = f(х), если f(х) ≥0; у = — f(х), если f(х)
Для любой функции у = f(х), если f(х) >0, то
| f (х)| = f(х), значит в этой части график функции
у = | f (х)| совпадает с графиком самой функции
Если же f(х) ) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика у = f(х).
Вывод: Гипотеза верна, действительно для построения графика функции
у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где
Вывод : Для построения графика функции у=|f (х) |
1.Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
5. График функции у=|f |(х)| |
Проверка истинности гипотез для графика функции у=|f |(х)| |
Применяя, определение абсолютной величины и ранее рассмотренные примеры построила графиков функции:
у = | |х³| — 2| и сделал выводы.
Для того чтобы построить график функции у = | f |(х)| надо:
1. Строить график функции у = f(х) для х>0.
2. Строить вторую часть графика, т. е. построенный график симметрично отражать относительно ОУ, т.к. данная функция четная.
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Построить график функции у = | 2|х | — 3| ( 1-й способ по определению модуля)
1. Строю у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х |>1,5 т.е. х 1,5
а) у = 2х — 3 , для х>0
2. Строю у = — 2 |х| + 3 , для 2|х | — 3
а)у = — 2х + 3 , для х>0
1) Строю у = 2х-3, для х>0.
2) Строю прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.
Сравнивая оба графика, видим, что они одинаковые.
1. Строю у = х² – 5 |х|, для х² – 5 |х| > 0 т.е. х >5 и х
а) у = х² – 5 х , для х>0
2. Строю у = — х² + 5 |х| , для х² – 5 |х|
а) у = — х² + 5 х , для х>0
а) Строю график функции у = х² – 5 х для х>0.
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.9)
1). Строю у = |х|³ — 2 , для |х|³ — 2 > 0, x> и x
а) у = х³ — 2 , для х>0
2). Строю у = — |х|³ + 2 , для |х|³ — 2
а) у = — х³ + 2 , для х>0
а) Строю у = х³ -2 для х > 0.
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.10)
При выполнении исследовательской работы я делала такие выводы:
— сформировала алгоритмы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
Алгоритм построения графика функции у=f |(х)|
1.Построить график функции у=f (х) для х>0;
2.Построить для х
Алгоритм построения графика функции у=|f (х) |
1.Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f (х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
— приобрела опыт построения графиков таких функций, как:
у=f |(х)|; у = | f (х)| ; у=|f |(х)| |;
— научилось работать с дополнительной литературой и материалами, производить отбор
— приобрела опыт выполнения графических работ на компьютере.
- И. М.Гельфанд, Е.Г. Глаголева. Функции и графики. Издательство «Наука»
- Р.А. Калнин. Алгебра и элементарные функции. Издательство «Наука»
- М.К. Потапов, С.Н. Олехник. Конкурсные задачи по математики, Москва. «Наука»
- Ю. Н.Макарычев, Н.Г. Миндюк. Дополнительные главы к школьному учебнику.
Предварительный просмотр:
Подписи к слайдам:
«Исследовательская работа по построению графиков функции, аналитическое выражение которых содержит знак абсолютной величины» Выполнила: Мухаматдинова Динара , ученик 10 класса Кучуковской средней общеобразовательной школы Агрызского муниципального района РТ Научный руководитель: Бурганиева А. Р., у читель математики высшей категории
Цель и задачи работы: изучить соответствующие теоретические материалы, выявить алгоритм построения графиков функции, аналитическое выражение которых содержит знак абсолютной величины. Объект исследования : функции, содержащие знак абсолютной величины. Предмет исследования: закономерность графиков функции у = f |(х)|, у = | f (х)|, у = | f |(х)| |. Методы исследования: решение примеров на построения графиков, сравнение, анализ, обобщение.
Содержание 1.Историческая справка 2.Геометрическая интерпретация понятия |а | 3.График функции у = f |(х)| 4.График функции у = | f (х)| 5.График функции у = | f |(х)| | 6.Выводы. 7.Список литературы.
В первой половине XVII века начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма(1601-1665) и Рене Декарт (1596-1650) представляли себе функцию как зависимость ординаты точки кривой от её абсциссы. А английский ученый Исаак Ньютон(1643-1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки. Историческая справка
Термин «функция» (от латинского function – исполнение , совершение) впервые ввел немецкий математик Готфрид Лейбниц(1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли(1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер(1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
Слово «модуль» произошло от латинского слова « modulus », что в переводе означает «мера». Это многозначное слово(омоним),которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках. В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Каждому действительному числу можно поставить в соответствие точку числовой прямой, это точка будет геометрическим изображением данного действительного числа. Каждой точке числовой прямой соответствует её расстояние от начало отсчета, или длина отрезка, начало которого в точке начала отсчета, а конец – в данной точке. Длина отрезка всегда рассматривается как величина неотрицательная. Геометрической интерпретацией действительного числа служит вектор, выходящий из начала отсчета и имеющий конец в точке, изображающей данное число. Длина этого вектора будет геометрической интерпретацией модуля данного действительного числа. Определение. Модуль числа a или абсолютная величина числа a равна a , если a больше или равно нулю и равна — a , если a меньше нуля: Геометрическая интерпретация понятия модуля |а| -а 0 а
Исследование графиков функции: 1. График функции у = f |(х)| 2. График функции у = | f (х)| 3. График функции у = | f |(х)| | 1.Анализ изученной литературы, построение графиков функции 2.Выдвижение гипотезы 3.Проверка гипотезы 4.Доказательство 5.Выводы
График функции у = |х| а) Если х≥0, то |х| = х и наша функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х 0; 2. Для х 0; 2. Для х 0 и симметрично отражённой частью у = f(х) при у 0, то | f (х)| = f(х), значит в этой части график функции у = | f (х)| совпадает с графиком самой функции у = f(х). Если же f(х) 0. 2. Строим вторую часть графика, т. е. построенный график симметрично отражаем относительно ОУ, т.к. данная функция четная. 3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Построить график функции у = | 2|х | — 3| 1. Строю у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х | >1,5 т.е. х 1,5 а) у = 2х — 3 , для х > 0 б) д ля х 0 б) д ля х 0. 2) Строю прямую, симметричную построенной относительно оси ОУ. 3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ. Сравнивая оба графика, видим что они одинаковые.
у = | х ² – 5|х| | 1. Строю у = х ² – 5 | х| , для х ² – 5 |х| > 0 т.е. х > 5 и х 0 б) д ля х 0 б) д ля х 0. б) Строю часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.
3. у =| |х| ³ — 2 | 1). Строю у = |х| ³ — 2 , для |х| ³ — 2 > 0 , x> и x 0 б) д ля х 0 б) д ля х 0. б) Строю часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Заключение При выполнении исследовательской работы я c делал такие выводы: — сформировал алгоритмы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины; — приобрел опыт построения графиков таких функций, как: у = f |(х)|; у = | f (х)|; у = |f |(х)||; — научился работать с дополнительной литературой и материалами, производить отбор научных сведений; выдвигал гипотезы и доказала истинность гипотез, сделал выводы; — приобрел опыт выполнения графических работ на компьютере.
Для построения графика функции у = f |(х)|: 1.Построить график функции у = f (х) для х>0; 2.Построить для х 0. 2. Строим вторую часть графика, т. е. построенный график симметрично отражаем относительно ОУ 3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ. Выводы
у = f |(х)| у = | f (х)| у = | f |(х)| | у = f (х), х>0 Построить часть для х 0 Выводы
Список литературы: И. М.Гельфанд, Е.Г. Глаголева. Функции и графики. Издательство «Наука» Р.А. Калнин. Алгебра и элементарные функции. Издательство «Наука» М.К. Потапов, С.Н. Олехник. Конкурсные задачи по математики, Москва. «Наука» Ю. Н.Макарычев, Н.Г. Миндюк. Дополнительные главы к школьному учебнику. Москва, «Просвещение».
Источник

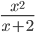 ≡ x^2/(x+2)
≡ x^2/(x+2) 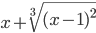 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3) 



