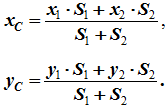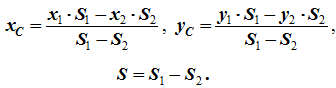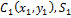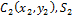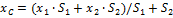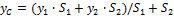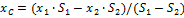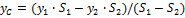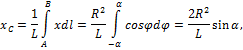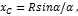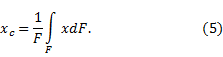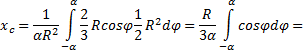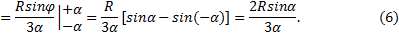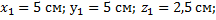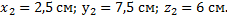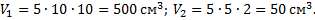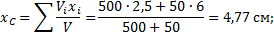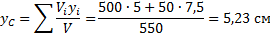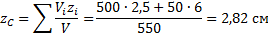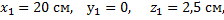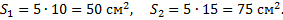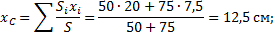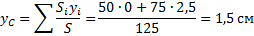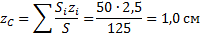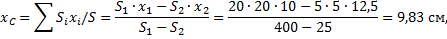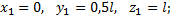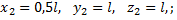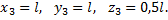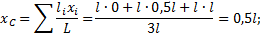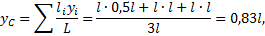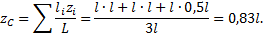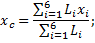iSopromat.ru
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов:
- Аналитический (путем интегрирования).
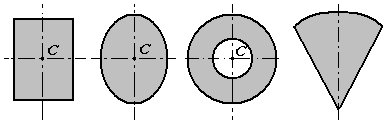
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел.
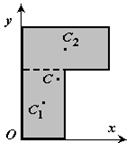
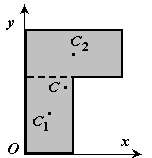
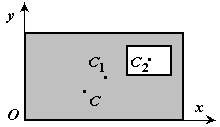
Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1+ S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
Дополнение (Метод отрицательных площадей или объемов).
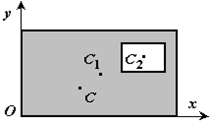
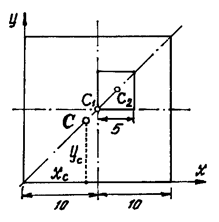
Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Определение центра тяжести плоской фигуры
методическая разработка
Определение центра тяжести плоской фигуры. В разработке указан способ определения центра тяжести аналитическим образом. Разработка будет полезна студентам для осовения практических умений по дисциплине «Техническая механика».
Скачать:
| Вложение | Размер |
|---|---|
| metodicheskaya_razrabotka_tsentr_tyazhesti_ploskoy_figury.docx | 165.39 КБ |
Предварительный просмотр:
Определение центра тяжести плоской фигуры
Центр тяжести применяется при исследовании устойчивости положений равновесия тел и сплошных сред, находящихся под действием сил тяжести и в некоторых других случаях, а именно: в сопротивлении материалов и в строительной механике – при использовании правила Верещагина.
При определении координат центра тяжести используются следующие методы:
1) метод симметрии: если сечение имеет центр симметрии или ось симметрии, то центр тяжести находится в центре симметрии или на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых, легко определить;
3) метод отрицательных площадей: этот способ является частным случаем способа разделения. Он используется, когда сечение имеет вырезы, срезы, полости (отверстия), которые рассматриваются как часть сечения с отрицательной площадью.
При решении задач на определение центра тяжести сложных сечений следует придерживаться следующего порядка:
1. Выбрать метод, который наиболее применим к данной задаче.
2. Разбить сложное сечение на простые части, для которых центры тяжести известны.
3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии.
4. Определить координаты центров тяжести отдельных частей относительно выбранных осей.
5. Используя формулы определить искомые координаты центра тяжести заданного сечения.

где А 1 , А 2 . Аn — площади простых сечений;
x 1 , x 2 … x n , y 1 , y 2 … y n – координаты центра тяжести простых сечений.
Координаты центра тяжести сложной плоской фигуры определяются после разделения ее на простые фигуры и определения их центров тяжести.
Координаты центра тяжести некоторых простых плоских фигур:
Порядок выполнения задания:
1) начертить заданное сложное сечение (фигуру), выбрать оси координат.
2) разбить сложное сечение на простые, для которых центры тяжести и силы тяжести известны;
3) определить необходимые данные для простых сечений:
4) определить координаты центров тяжести простых сечений относительно выбранных осей координат;
5) определить положение центра тяжести сложного сечения.
Найти координаты центра тяжести плоской фигуры, изображенной на рисунке.
Выбираем оси координат так, чтобы нижний и левый край фигуры совпали с ними:
Делим заданную плоскую фигуру на прямоугольник (1), треугольник (2) и круг (3).
Вычисляем площади этих фигур:
S 1 = 10·20 = 200; S 2 = 0,5·5·10 = 25; S 3 = π·9 =28,3.
Определяем координаты центров тяжести фигур:
x 2 = 5; y 2 = 11,7.
Координаты центра тяжести всей плоской фигуры:
По теме: методические разработки, презентации и конспекты
Проецирование плоских фигур
Методическая разработка по теме Проецирование плоских фигурпо дисциплине инженерная графика. Краткое содержание материала, тестовое задание по теме, задание на графическую работу.
Методическая разработка «Сценарий интегрированного занятия Математика + Информатика «Вычисление площади плоской фигуры с помощью определенного интеграла»
Интегрированный урок — это учебное занятие, на котором тема рассматривается с различных точек зрения, средствами нескольких дисциплин. Интегрированные уроки формируют познавательный интерес обучающихс.
Методическая разработка урока по технической механике «Определение центра тяжести плоской фигуры»
Данная методическая разработка содержит методические указания по проведению лабораторной работы «Определение центра тяжести плоской фигуры».
План — конспект урока на тему Центр тяжести для студентов СПО
ГБПОУ «Навашинский политехнический техникум», Россия, Глебова Ю.В., 2012 г., 12 стр., 76 слайдов; Описание: План-конспект урока по дисциплине «Техническая механика» на тему «Центр тяжести» для студент.
Творческая работа студента «Роль центра тяжести в машиностроении»
ГБПОУ «Навашинский судомеханический техникум»; Выполнил: Кирилов А.В. студент II курса; Руководитель: Глебова Ю.В.,преподаватель ; Исследовательская работа — 26 стр., , 2014 г. Практ.
Методические указания по выполнению лабораторной работы «Определение положения центра тяжести сечения» по дисциплине «Техническая механика»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИГосударственное бюджетное профессиональное образовательное учреждение «Кстовский нефтяной техникум имени Бориса Ивановича Корнилова»ОП-04Система.
Определение центра тяжести плоских фигур
решени задач на определение центра тяжести плоских фигур.
Источник
Способы определения координат центра тяжести.



Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.7
2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.
Рис.8
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.9
4. Метод группировки. Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы.
Центры тяжести некоторых однородных тел.
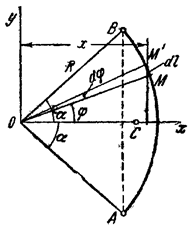
1) Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом 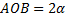
Рис.10
Найдем координату 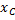
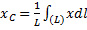
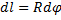
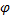
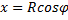
где L — длина дуги АВ, равная 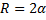
Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном
где угол 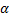
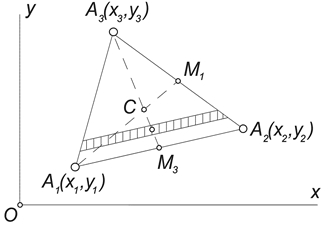
2) Центр тяжести площади треугольника. Рассмотрим треугольник, лежащий в плоскости Oxy, координаты вершин которого известны: Ai (xi,yi), (i = 1,2,3). Разбивая треугольник на узкие полоски, параллельные стороне А1А2 , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А3 М3 (рис.11).
Рис.11
Разбивая треугольник на полоски, параллельные стороне А2А3, можно убедиться, что он должен лежать на медиане А1М1. Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан, которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.
В частности, для медианы А1М1 получим, учитывая, что координаты точки М1 — это среднее арифметическое координат вершин А2 и А3 :
Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:
3) Центр тяжести площади кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2α, расположенный симметрично относительно оси Ox (рис.12) .
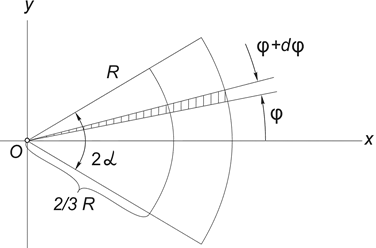
Очевидно, что yc = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле:
Рис.12
Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом dφ. С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R×dφ и высотой R. Площадь такого треугольника dF=(1/2)R 2 ?dφ, а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому в (5) положим x = (2/3)R?cosφ. Подставляя в (5) F = αR 2 , получим:
С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга.
Подставляя в (2) α = π/2, получим: xc = (4R)/(3π) ≅ 0,4R .
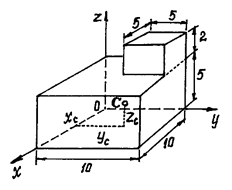
Пример 1. Определим центр тяжести однородного тела, изображённого на рис. 13.
Рис.13
Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:
Объёмы их:
Поэтому координаты центра тяжести тела
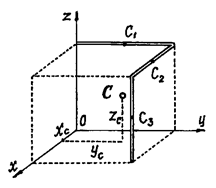
Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.14).
Рис.14
Координаты центров тяжести:
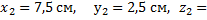
Площади:
Пример 3. У квадратного листа 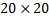
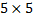
Рис.15
В этой задаче удобнее разделить тело на две части: большой квадрат и квадратное отверстие. Только площадь отверстия надо считать отрицательной. Тогда координаты центра тяжести листа с отверстием:

координата 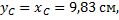
Пример 4. Проволочная скобка (рис.16) состоит из трёх участков одинаковой длины l.
Рис.16
Координаты центров тяжести участков:
Поэтому координаты центра тяжести всей скобки:
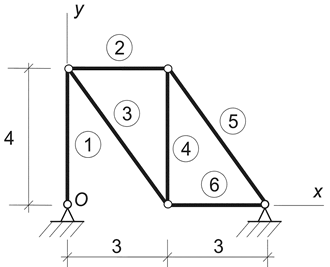
Пример 5. Определить положение центра тяжести фермы, все стержни которой имеют одинаковую погонную плотность (рис.17).
Напомним, что в физике плотность тела ρ и его удельный вес g связаны соотношением: γ= ρg , где g — ускорение свободного падения. Чтобы найти массу такого однородного тела, нужно плотность умножить на его объем.
Рис.17
Термин «линейная» или «погонная» плотность означает, что для определения массы стержня фермы нужно погонную плотность умножить на длину этого стержня.
Для решения задачи можно воспользоваться методом разбиения. Представив заданную ферму в виде суммы 6 отдельных стержней, получим:
где Li длина i-го стержня фермы, а xi, yi — координаты его центра тяжести.
Решение этой задачи можно упростить, если сгруппировать 5 последних стержней фермы. Нетрудно видеть, что они образуют фигуру, имеющую центр симметрии, расположенный посредине четвертого стержня, где и находится центр тяжести этой группы стержней.
Таким образом, заданную ферму можно представить комбинацией всего двух групп стержней.
Первая группа состоит из первого стержня, для нее L1 = 4 м, x1 = 0 м, y1= 2 м. Вторая группа стержней состоит из пяти стержней, для нее L2 = 20 м, x2= 3 м, y2= 2 м.
Координаты центра тяжести фермы находим по формуле:
Вопросы для самопроверки
— Что называется центром параллельных сил?
— Как определяются координаты центра параллельных сил?
— Как определить центр параллельных сил, равнодействующая которых равна нулю?
— Каким свойством обладает центр параллельных сил?
— По каким формулам вычисляются координаты центра параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?
— Что называют статическим моментом площади?
— Приведите пример тела, центр тяжести которого расположен вне тела.
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных весов?
— Где расположен центр тяжести дуги окружности?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести кругового сектора.
— Используя формулы, определяющие центры тяжести треугольника и кругового сектора, выведите аналогичную формулу для кругового сегмента.
— По каким формулам вычисляются координаты центров тяжести однородных тел, плоских фигур и линий?
— Что называется статическим моментом площади плоской фигуры относительно оси, как он вычисляется и какую размерность имеет?
— Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?
— Какими вспомогательными теоремами пользуются при определении положения центра тяжести?
Источник