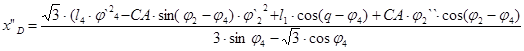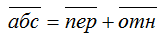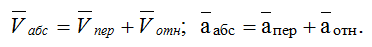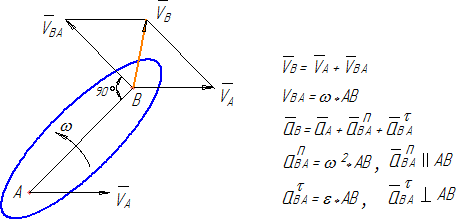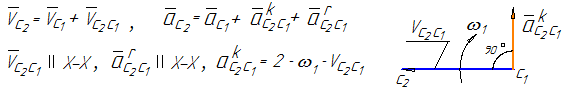Аналитическое определение аналогов скоростей и ускорений.
А) Для определения аналогов скоростей берутся первые производные от групповых уравнений по обобщённой координате (q), для первой группы:
, (5.1)
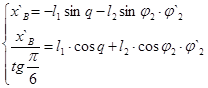
Корни уравнений находятся по метод Крамера:
, (5.2)
. (5.3)
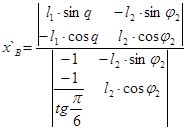
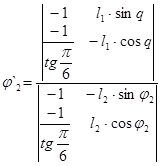
Решение в общем виде:
– аналог скорости точки В, (5.4)
– аналог угловой скорости звена 2. (5.5)
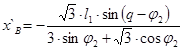
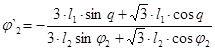
Значение аналога скорости точки В и аналога угловой скорости звена 2 при входной координате q=30°:
Б) Аналогичный расчёт производится для второй группы:
, (5.6)
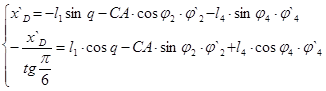
Корни уравнений находятся по метод Крамера:
, (5.7)
. (5.8)
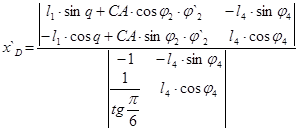
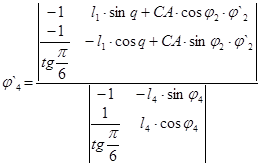
Решение в общем виде:
– аналог скорости точки D, (5.9)
– аналог угловой скорости звена 4. (5.10)
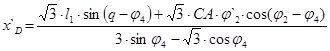
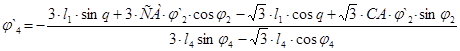
Значение аналога скорости точки В и аналога угловой скорости звена 2 при входной координате q=30°:
В) Для определения аналогов ускорений берутся вторые производные от групповых уравнений по обобщённой координате (q), для первой группы:
, (5.11)
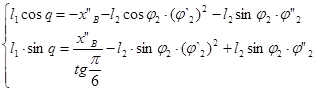
Корни уравнений находятся по метод Крамера:
, (5.12)
. (5.13)
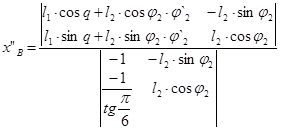
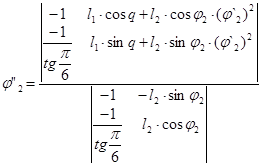
Решение в общем виде:
– аналог ускорения точки В, (5.14)
– аналог углового ускорения звена 2. (5.15)
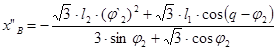
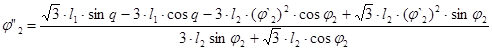
Значение аналога ускорения точки В и аналога углового ускорения звена 2 при входной координате q=30°:
Г) Аналогичный расчёт производится для второй группы:
,(5.16)
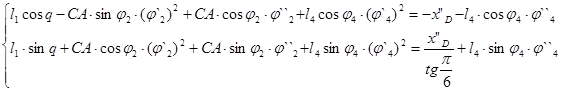
Корни уравнений находятся по метод Крамера:
, (5.17)
. (5.18)
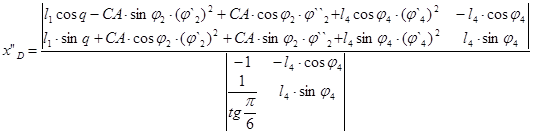
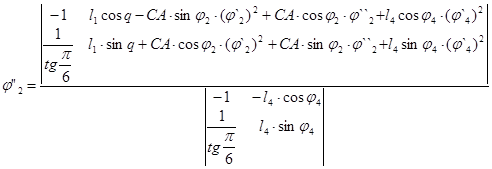
Решение в общем виде:
– аналог ускорения точки D, (5.19)
– аналог углового ускорения звена 4. (5.20)
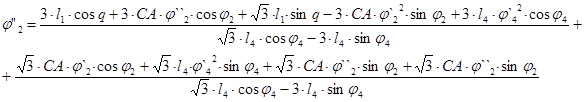
Значение аналога ускорения точки D и аналога углового ускорения звена 4 при входной координате q=30°:
Источник
Аналитическое определение скоростей и ускорений
Аналитическое определение скоростей и ускорений
- Изложенные графические методы определения скоростей и ускорений просты, наглядны и быстро приводят к цели. Однако как бы тщательно* ни выполнялись построения планов, всегда приходится считаться с недостатком, свойственным графическим методам: трудно установить, какая точность результатов достигается.
В тех случаях, когда расчет должен быть особенно точным, и когда точность расчета задается заранее, пути, скорости и ускорения могут быть определены аналитически. Аналитическое определение путей, скоростей и ускорений всегда является возможным, так как механизм во всяком положении представляет собой замкнутую фигуру, для определения сторон и углов которой всегда имеется
достаточно данных. Однако уравнения, к которым приводят аналитические Людмила Фирмаль
методы, получаются часто сложными и потому неудобными для практического использования при анализе даже самых простых механизмов. В предыдущем параграфе, применяя графические методы, мы получили три кривые, выражающие пути, скорости и ускорения точки С механизма, изображенного схематически на фиг. 53, а, в функциях угла поворота кривошипа или времени его поворота от
начального положения. При применении аналитических методов мы вместо кривых должны получить уравнения, выражающие те же зависимости, какие выражаются кривыми.Аналитическое определение скоростей и ускорений 45 Примем для изображенного на фиг. 54 кривошипно-шатунного механизма следующие обозначения: ср — угол поворота кривошипа АВ, отсчитываемый от начального положения кривошипа ЛВ0 по часовой стрелке; Z,— длина
- кривошипа АВ\ 12 — длина шатуна ВС\ s = CQC — путь, пройденный точкой С от начального положения Со за время поворота кривошипа на угол ср. Для получения уравнения кривой путей выразим s в функции Людмила Фирмаль
упрощения уравнение кривой скоростей в виде ds
di sin 2 со/ 2 «Kp2 — sin2 со/ (О.46 Кинематический анализ плоских механизмов Дифференцируя последнее уравнение, получаем после упрощения уравнение кривой ускорений в виде cos 2соt sin2 2
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
iSopromat.ru
Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов в теории механизмов и машин.
Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.
Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное — движение данной точки относительно той, движение которой принято за переносное:
Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:
Планы скоростей и ускорений обладают следующими свойствами:
- на плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана. На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает;
- отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек. Вектор относительной скорости направлен на плане к той точке, которая в индексе скорости стоит на первом месте;
- фигуры, образованные точками одного и того же жесткого звена на плане и на механизме, подобны. Поэтому, если на звене известны скорости и ускорения двух точек, то скорость и ускорение любой третьей точки этого же звена можно найти по подобию;
- имея план скоростей, можно найти угловую скорость любого звена механизма. Для определения угловой скорости исследуемого звена надо взять относительную скорость двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
- имея план ускорений, можно найти угловое ускорение любого звена механизма. Для определения углового ускорения исследуемого звена надо взять тангенциальную составляющую относительного ускорения двух любых точек данного звена и разделить на расстояние между этими точками на механизме;
- звенья, соединенные в поступательнуюкинематическую пару, имеют одинаковые угловые скорости и одинаковые угловые ускорения.
При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:
1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).
В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.
Для примера, приведенного на рисунке 13, нормальное ускорение точки В относительно точки А будет направлено вдоль радиуса ВА к точке А. Тангенциальное – перпендикулярно этому радиусу;
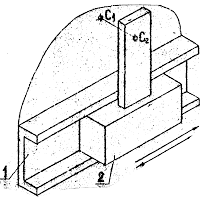
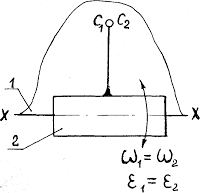
2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей (рисунок 14).
Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С1, принадлежащей этой направляющей.
Движение точки С1 принимается в качестве переносного. Движение точки С2, принадлежащей ползуну, относительно точки С1 получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С1 и С2 совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).
Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится.
Уравнения планов для групп Ассура второго класса приведены в таблице 3.1.
Таблица 3.1 – Кинематический анализ групп Ассура II класса методом планов
Источник
