Аналитический способ определения погрешности

Аналитические методы определения погрешностей

13.2. Аналитические методы определения погрешностей

13.2.1. Сущность аналитических методов заключается в том, что погрешность любого параметра обычно намного меньше самого параметра, поэтому погрешность можно представить как дифференциал переменной, а для определения погрешности совокупности параметров (например, функции положения) использовать математический аппарат функций многих переменных.

13.2.2. Дифференциальный метод определения абсолютных погрешностей. Совокупность связанных геометрических параметров (q) i (размерную цепь, функцию положения и т.п.) представляют функцией этих параметров, считая их переменными:

psi = F (q1, q2. qn ) . (13.1)

Погрешности размеров del (q)i приравнивают к дифференциалам этих параметров: del (q)i = d (q)i, а дифференциал функции — к погрешности функции:

del (psi) = (dF/dq1) *del (q1) + (dF/dq2) *del (q2) +.

. + (dF/dqn) *del (qn) = sum[ (dF/dqi) *del (qi) ]1, n . (13.2)

Слагаемые (dF/dqi) *del (qi) — частичные погрешности за счет погрешностей первичных параметров qi .

Дифференциальный метод определения погрешностей универсален, он может быть применен практически к любому М. Например, для шарнирно-ползунного М (рис. 13.1) функция положения

Погрешность положения М:

del (s) = (ds/dr) *del (r) + (ds/dl) *del (l) + (ds/dh) *del (h) .

13.2.3. Определение относительных погрешностей с использованием дифференциального метода. Из выражения (13.2) следует, что относительная

погрешность ddel (psi) функции psi = F (qi) :

ddel (psi) = del (psi) /psi —> dpsi/psi =

= (dlnF/dq1) *del (q1) + (dlnF/dq2) *del (q2) + .

. + (dlnF/dqn) *del (qn) = sum[ (*dlnF/dqi) *del (qi) ]1, n . (13.3)

Относительная погрешность для функции psi = F (qi), которая может быть представлена как произведение функций psi = П[f (qi) ]1, n:

ddel (psi) = sum|[qi/[f (qi) ]k*<[d[f (qi) ]k/dqi>*del (qi) |1, n . (13.4)

Например, для аксоидного М (рис. 13.2), для которого передаточное отношение (i) 1, 6 = (d2*d4*d6) / (d1*d3*d5) относительная погрешность определяется выражением

ddel[ (i)1, 6] = ddel (d1) + ddel (d2) + ddel (d3) +

+ ddel (d4) + ddel (d5) + ddel (d6) .

13.3. Экспериментальный метод определения погрешностей

Погрешности положения или перемещения измеряют во всем диапазоне на реальном М. В результате получают суммарное значение погрешности схемы и технологической (рис.13.4) : del (psi) сум = del (psi) сх + del (psi) т .

Эту сумму можно разделить на составляющие, измерив параметры серии одинаковых изделий и усреднив результаты. Технологические погрешности — случайные величины — в этом случае компенсируют друг друга, и из общей погрешности выделяется погрешность схемы del (psi) сх (рис. 13.3) .

13.5. Методы достижения заданной точности параметров

13.5.1. При создании М применяют различные методы достижения заданной точности результирующего параметра, обеспечивающей функциональную В3 (для замыкающего звена размерной цепи, кинематической погрешности и т.п.) . Это методы полной и неполной В3, и компенсационные — групповой ВЗ, пригонки, регулирования.

13.5.2. Метод полной В3: требуемая точность результирующего параметра достигается у всех обьектов без выбора, подбора или изменения значений составляющих параметров. Например, сборка М из деталей, у каждой из которых отклонения размеров не превышают допустимых.

Значения погрешности результирующего параметра расчитывают методом максимума-минимума, учитывая предельные отклонение составляющих параметров и самые неблагоприятные их сочетания:

del (psi) = sum|[dF/d (qi) ]*del (qi) | . (13.5)

13.5.3. Метод неполной В3: требуемая точность результирующего параметра достигается у заранее обусловленной части обьектов без выбора, подбора или изменения составляющих параметров. При этом часть собраных М будет непригодной по условию В3, однако за счет уменьшения точности изготовления деталей общие затраты средств на всю партию изделий снижаются по сравнению с методом полной В3. Расчет значения погрешности результирующего параметра производят вероятностным методом:

где (Ev) qi — координата середины поля рассеяния погрешности параметра

qi ; (V) qi — поле рассеяния погрешности этого параметра; t — веро ятностный коэффициент, учитываюющий процент риска выхода погрешно сти del (psi) за допустимые пределы.

13.5.4. Метод групповой В3: точность результирующего параметра достигается сборкой М из групп звеньев с погрешностями, компенсирующими друг друга, для чего звенья предварительно рассортировывают на группы, имеющие близкие значения отклонений параметров. Метод особенно эффективен при изготовлении изделий большими сериями или при массовом производстве.

13.5.5. Метод пригонки: требуемая точность результирующего параметра достигается изменением размера звена-компенсатора путем удаления с него определенного слоя материала. Компенсирующее звено должно быть предусмотрено в конструкции соответствующего узла М. Этим методом например, обеспечивают необходимые зазоры в М, дорабатывая по толщине специальные прокладки или кольца.

13.5.6. Метод регулирования: точность результирующего параметра достигается изменением размера компенсирующего звена без удаления с него материала. Звено-компенсатор должно иметь конструкцию, позволяющую регулировать его размеры. Например, момент противодействующей пружины стрелочного электроизмерительного прибора регулируют специальным винтом.

Источник

3.4.2 Расчетно-аналитический метод определения суммарной погрешности

Определение суммарной операционной погрешности по этому методу выполняется в следующей последовательности:

а) Изучение условий выполнения операций (способа обработки, способа выполнения размера, характеристик станка, режущего имерительного инструментов, режимов резания и т. д.);

б) Выявление и составление перечня факторов, обусловливающих появление первичных (элементарных) погрешностей обработки и установки;

в) Определение значений первичных (элементарных) погрешностей, вызываемых действием каждого из факторов, внесенных в перечень. В большинстве случаев задача будет заключаться в определении поля погрешности. При решении этой задачи можно применить аналитический (расчетный) метод, используя приведенные в разд. 3.1-3.3 формулы и зависимости и аналогичные им. В тех случаях, когда для определения какой либо первичной погрешности аналитические зависимости еще не установлены, величину такой погрешности принимают по нормативным или справочным данным (например, погрешность установки деталей в патроне, в тисках и т. п.);

г) Установление законов распределения для каждой из первичных погрешностей обработки и установки. Найденные (вычисленные, принятые по справочным и нормативным источникам) первичные погрешности нельзя просто сложить арифметически, полученная при таком суммировании величина операционной погрешности будет значительно больше действительной. Это можно объяснить тем, что каждая из первичных погрешностей определялась для экстремальных (худших) условий и является предельной максимально возможной. Но сочетание худших условий по всем погрешностям при обработке каждой детали мало вероятно.

Достоверное значение суммарной погрешности можно получить, если суммирование первичных погрешностей выполнять по правилам теории вероятностей и математической статистики. Эти правила заключаются в следующем:

1. Случайные погрешности, подчиняющиеся закону нормального распределения, складываются по правилу квадратичного корня.

2. Случайные погрешности, не подчиняющиеся закону нормального распределения, и закономерно изменяющиеся погрешности суммируются с учетом закона их распределения.

3. Систематические постоянные погрешности между собой складываются алгебраически с учетом их знака. При определении суммарной погрешности для генеральной совокупности постоянные сис­тематические погрешности со случайными и закономерно изменяющимися суммируются арифметически.

При этом суммарная погрешность может быть определена по формуле

. (3.15)

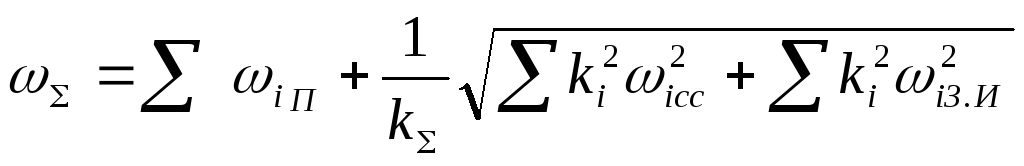
Где к₁и к_∑коэффициенты относительного рассеивания первичных погрешностей и их сумм.

Статистический метод определения суммарной погрешности

Содержанием статистического метода является измерение размера (или другого параметра) деталей анализируемой совокупности, вычисление характеристик распределения, построение практической кривой распределения, анализ кривой и характеристик распределения и выбор на этой основе теоретического закона распределения анализируемой совокупности. Все эти данные позволяют вычислить составляющие суммарной погрешности и всю погрешность.

При статистическом анализе точности необходимо соблюдение следующих требований:

а) для анализа брать детали, изготовленные при стабильных условиях, т. е. одним размерным инструментом до его переточки или при одной наладке станка (между двумя подналадками);

б) число деталей в совокупности должно быть значительным. Чем больше взято деталей для анализа, тем с большей достоверностью будут определены характеристики распределения;

в) измерение деталей должно выполняться инструментом, ценаделения которого должна быть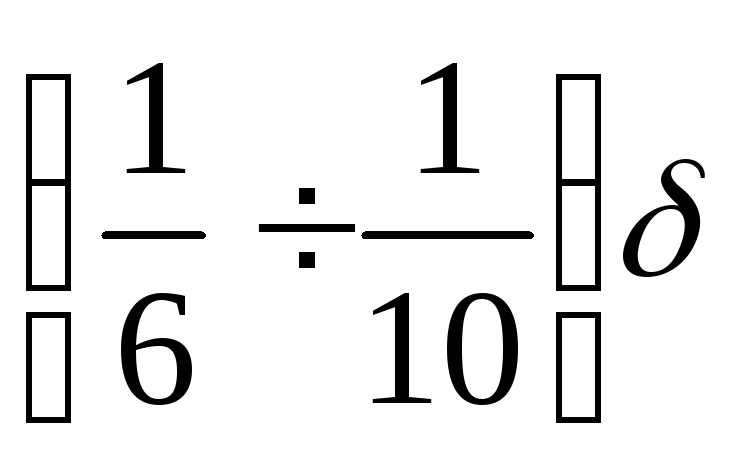, гдеδ — допуск на измеряемый размер.

Содержание всех этапов статистического метода определения операционной погрешности рассмотрим на примере. На автомате с выдерживанием размеров по настройке была изготовлена партия роликов D = 20_-0,2 в количестве N=100 штук. Размеры деталей занесены в таблицу измерений (табл.2). Пользуясь данными таблицы, вычисляем практическое поле рассеивания (размах варьирования, широту распределения):

R=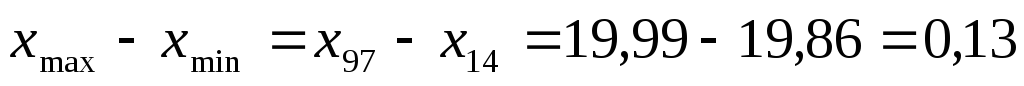мм

Таблица 2- Таблица размеров деталей, мм [7]

Для удобства обработки статистических данных и построения кривой распределения величину размаха разделяют на разряды (интервалы). Число разрядов k должно быть увязано с количеством деталей в совокупности: при N=50—100 шт.k=5—7, приN>100 k=7—11. Кроме того, число разрядов должно быть таким, чтобы цена разряда c=R/k была больше цены деления мерительного инструмента. Выполнение этого требования необходимо для того, чтобы уменьшить влияние погрешностей измерений. Примем для нашего примера k=7. Тогда расчетная цена разряда будет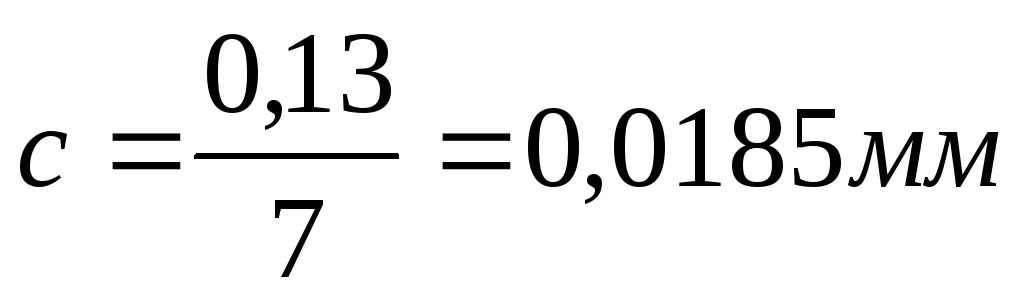. Примем с=0,02 мм. Заметим, что округление цены разряда должно быть минимальным и допустимо в большую сторону.

Для решения поставленной задачи необходимо вычислить главные характеристики распределения: статистический центр группирования или среднее арифметическое значение размера для совокупности х_сри среднее квадратичное отклонениеσ по уравнениям:

(3.16)

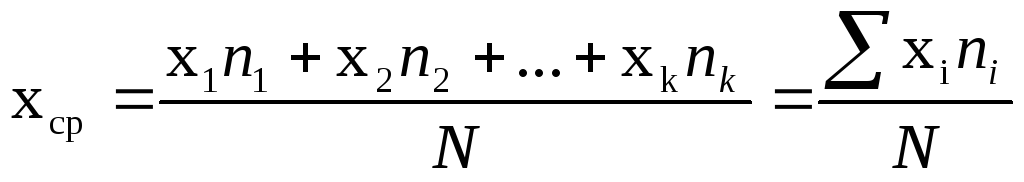
σ =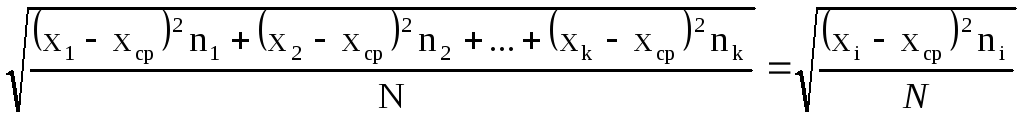(3.17)

В этих уравнениях x_i, x_2…x_k— значения представителей разрядов;

n₁, n₂. n_k — количество деталей (частота) в разряде. Важным является выбор границ между разрядами: они должны проходить не по измеренным значениям размеров, а между ними. Примем граничными значения x_i 19,855, 19,875 и т. д.

Результаты расчетов x_cр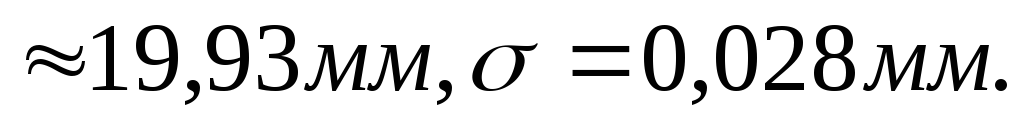

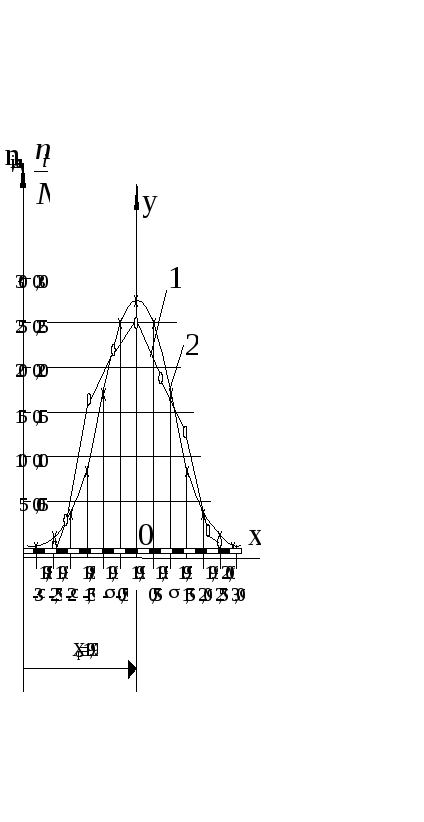
Рис.16 Практическая 1 и теоретическая 2 кривые распределения

Следующим этапом является построение практической кривой распределения. Она строится в координатах x_i, n_i. Масштабы по осям выбираются произвольные, удобные для построения. Практи­ческая кривая для нашего примера приведена на рис.16 (ломаная линия). При ее построении приняты масштабы: по оси x_i 0,01 мм соответствует 10 мм; по оси n_i 1 деталь — 2 мм. Построение кривой выполняется обычным путем: для всех значений х_i (19,87, 19,89 и т. д.) откладываются по вертикали в масштабе соответствующие им значения n_i. Полученные точки соединяются отрезками прямой.

Практическая кривая служит для первой приближенной оценки точности процесса, оценки «чистоты» эксперимента и правильности обработки результатов измерений и решения вопроса о выборе те­оретического закона для характеристики данного распределения. Приближенной же потому, что форма практической кривой распределения зависит не только от объективных причин — характера распределения размеров, но и от случайных — числа интервалов или разрядов k, количества принятых для анализа деталей N. В связи с этим, для объективной оценки точности обработки прак­тические кривые необходимо заменить теоретическими кривыми,изображающими вполне определенные законы распределения, за­даваемые математическими уравнениями.

В разд. 3.4.1 был сделан краткий обзор теоретических законов распределения. Возникает вопрос — какой из них следует исполь­зовать для характеристики распределения размеров обследован­ной партии деталей. Правильно будет при решении этого вопроса исходить из анализа условий обработки партии деталей и характеpaдействия причин, обусловивших распределение погрешностей.Многочисленные исследования показали, что при механической об­работке деталей на металлорежущих станках по способу автомати­ческого достижения заданных размеров (по настройке, с использо­ванием мерного режущего инструмента) распределение размеровподчиняется (в достаточной мере соответствует) закону нормально­го распределения. На этом основании примем этот закон для ха­рактеристики рассматриваемого в примере распределения разме­ров роликов D=20_-0,2.

Для распределения по этому закону, как отмечалось выше, при­нимают шестисигмовое поле рассеивания, т. е. принимают ω_ρ = 6σ. Для нашего примера: ω_ρ = 6σ = 6·0,028 = 0,168 мм. Следует обратить внимание на то, что теоретическая величина поля рассеивания оказалась значительно больше практического поля (размаха варьирования): 0,168>0,13 мм. Объясняется это тем, что размах варьиро­вания R = 0,13 мм характеризует точность конкретной партии с ко­личеством N=100 штук деталей. Теоретическое же поле рассеива­ния позволяет дать оценку метода обработки, прогнозировать точ­ность обработки сколько угодно большого числа деталей. Можно с большой достоверностью утверждать, что если по данному методу на данном станке, при поддержании на принятом уровне всех ос­тальных условий, обрабатывать детали в неограниченном количест­ве и неограниченное время, то поле рассеивания будет составлять

Теперь построим кривую нормального распределения, причем для возможности сопоставления и анализа будем строить ее совме­щенной с эмпирической кривой и согласуем их масштабы. По оси х для эмпирической кривой было принято 0,01→10 мм. Тогда длятеоретической кривой σ = 0,028→28 мм. Для увязки масштабов по оси ординат из условия равенства площадей под кривыми используем уравнение

, (3.18)

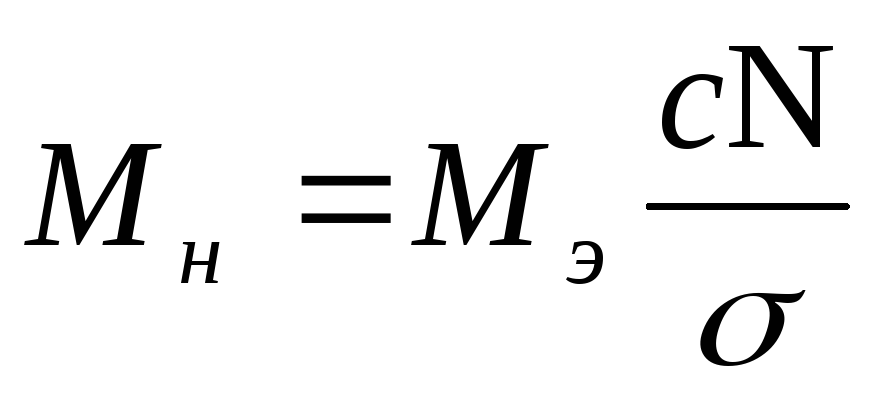
где М_ни М_э— масштабы соответственно для кривой нормальногораспределения и эмпирической кривой; с — цена разряда (ранее было принято с = 0,02 мм);Ν — число деталей в совокупности (Ν= 100). Для нашего примера

. (3.19)

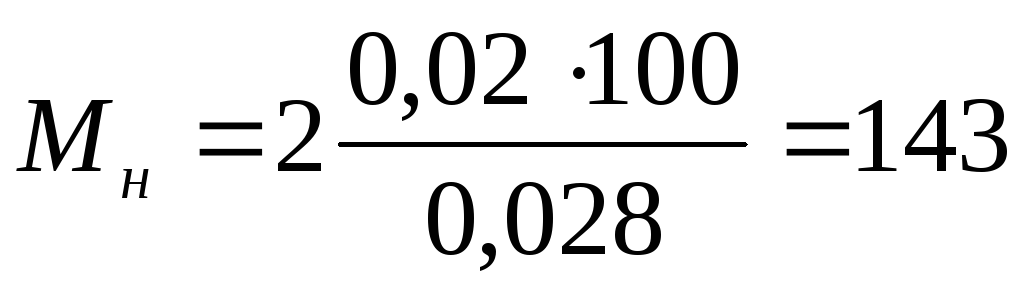
При построении кривой нормального распределения сначала откла­дывается ее ось, соответствующая x_cp= 19,93 мм. Это значение x принимается за начало отсчета точек на осиx в доляхσ. По осиу откладываются ординаты кривой нормального распределения. Для их определения нет необходимости производить каждый раз вычисления по уравнению кривой у=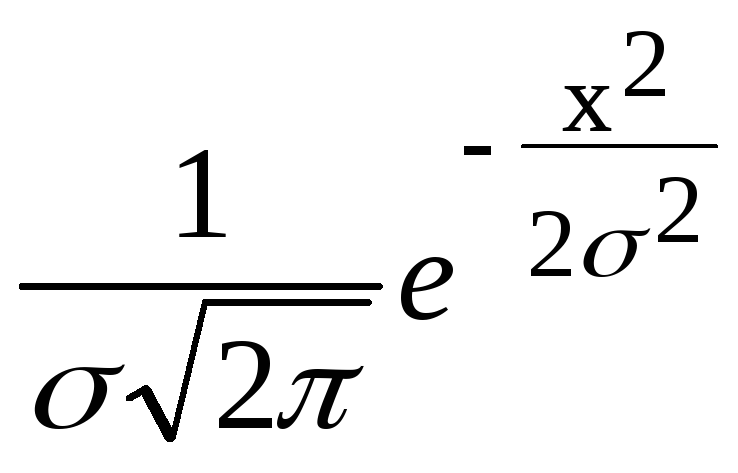, можно воспользоваться табличными значениями этой функции.

Сравнение эмпирической и нормальной кривых по степени совпадения их формы, площадей и положения, позволяет судить о характере влияния факторов процесса на погрешность изготовления детали.

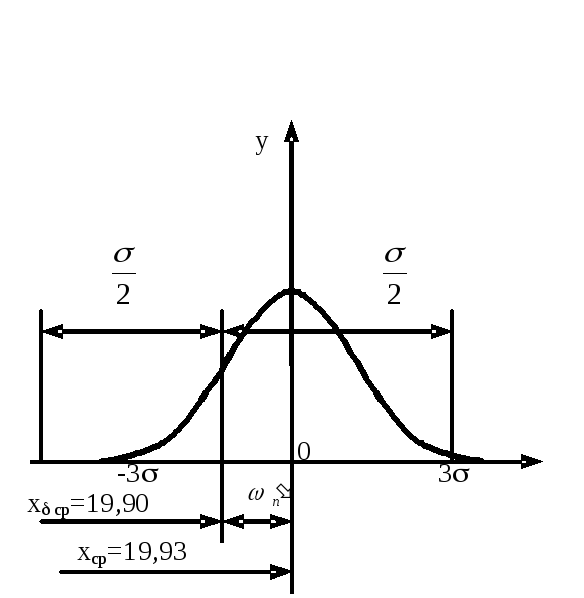
Выше была определена одна составляющая суммарной погрешности — ω_р=6σ. Перейдем теперь к определению другой составляющей — ω_п, учитывающей влияние постоянных систематических погрешностей. На рис.17 изображено поле допуска на размер обрабатываемых в примере деталей δ=0,2 мм с координатой его середины х_δср = 19,90 мм. В этом поле расположена в масштабе кривая нормального распределения для нашего эксперимента с координатой середины поля рассеивания х_ср= 19,93. Из схемы и сопоставления х_δср и х_ср следует, что ось кривой распределения смещена с середины поля допуска за счет влияния постоянных систематических погрешностей на величину:

(3.20)

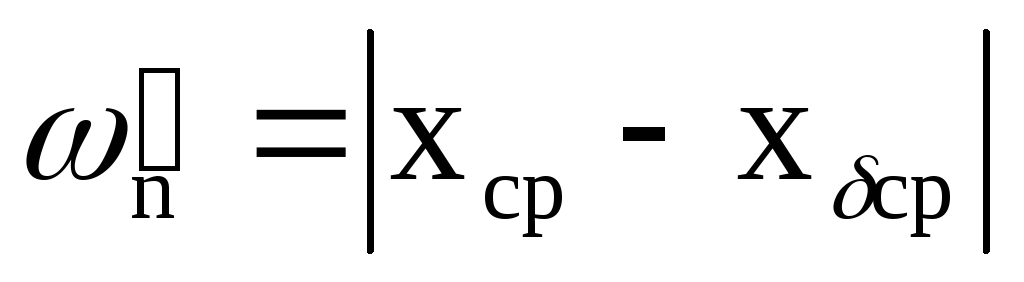
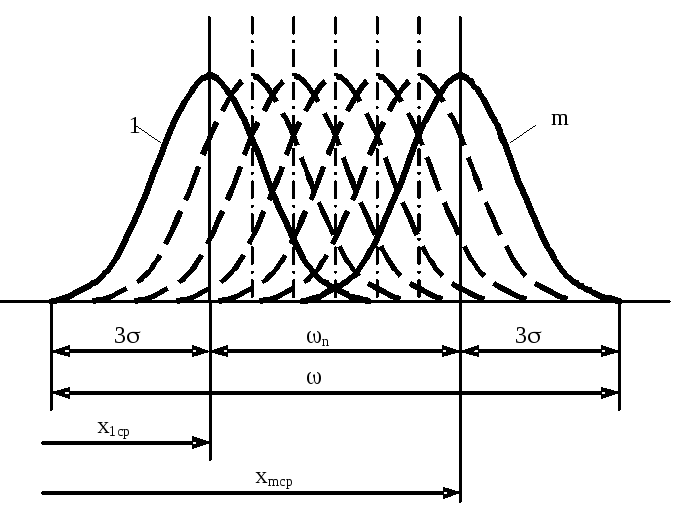
Для нашего примера ω_п‘ = 19,93—19,90 = 0,03 мм. Величина ω_п‘ характеризует направление и степень влияния постоянных систематических факторов, действовавших (имевших место) при обработке анализируемой партии деталей. Обычно для производственных и научных целей основным является определение точностных характеристик не отдельной партии деталей, а метода обработки, т.е. генеральной совокупности деталей. Генеральная совокупность(склад) включает детали многих партий, изготовляемых в разное время, на разных станках и при разных наладках (или разными мерными инструментами). Если для каждой партии вычислить ха­рактеристики распределения и для всех партий построить кривые распределения — получилась бы не одна, а семейство кривых, расположенных как показано на рис. 18.

По этой схеме становится очевидной структура уравнения (3.15):ω=ω_п+ω_р= ω_п+6σ.

Рис.17 Влияние постоянной погрешности на положение кривой распределения в поле допуска

Рис.18 Схема к определению ω_п

При этом величина постоянной составляющей может быть, определена по формуле:

_(3.21)

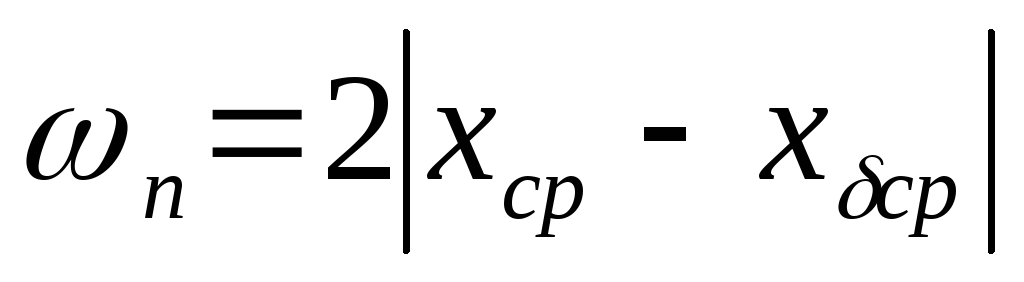
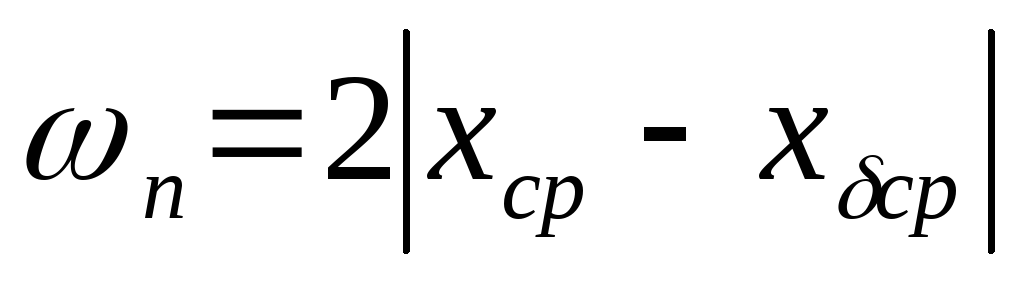
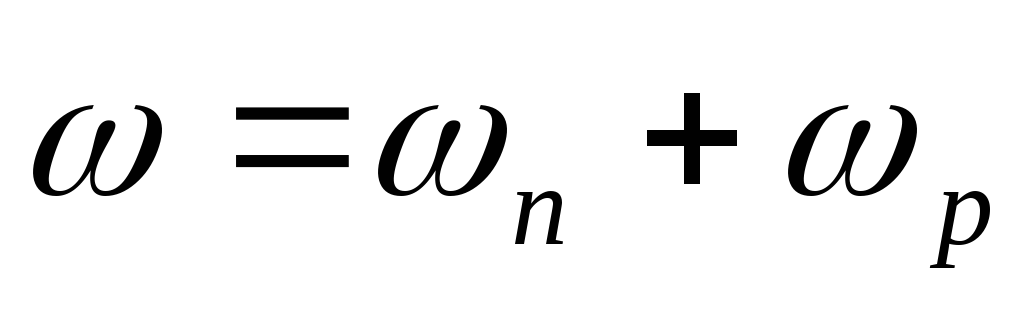
Используем это уравнение для оценки влияния постоянных систематических факторов по данным нашего примера: = =2(19,93—19,90) =0,06 мм. Тогда, в соответствии с уравнением (3.15) суммарная погрешность использованного в примере метода обработки будет= 0,06 + 0,168 = 0,228 мм. Вычисленная величина ω превышает допуск на выполняемый размер: 0,228>0,20 мм. Следовательно, хотя в экспериментальной партии все N=100 штук деталей имели размеры в пределах допуска (см. табл.2), при использовании этого метода в последующем, при обработке неограниченно большого количества деталей, возможен выход размеров части деталей за пределы поля допуска.

Рассмотрим теперь использование результатов статистического анализа и метода кривых распределения.

По форме эмпирической кривой распределения можно судить о доминирующем закономерно изменяющемся факторе. Например, кривая со скругленной, плоской вершиной будет свидетельствовать о большом влиянии размерного износа инструмента. Получение двухвершинной кривой для деталей, обработанных при одной настройке (одним мерным инструментом) указывает на то, что в какой то момент обработки в действие включился непредвиденный постоянный фактор —сбилось положение инструмента и т. п. По положению центра группирования в поле допуска, т. е. по величине 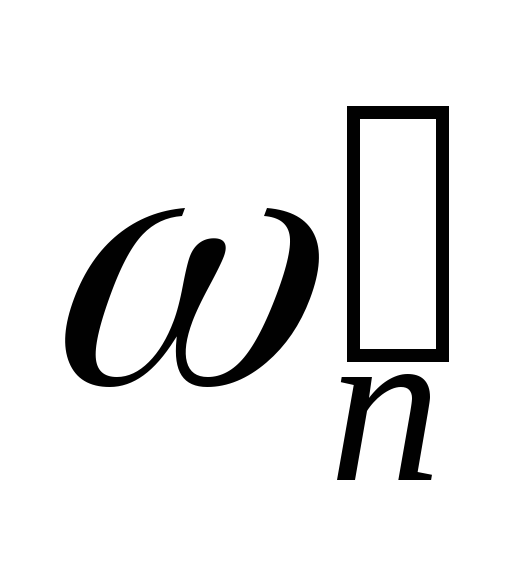можносудить о качестве настройки станка или о соответствии размера мерного инструмента заданному значению.

По соотношению поля рассеивания ω_р = 6σ и поля допуска σ можно судить, о возможности обработки деталей по настройке и о до­пуске на настройку.

В тех случаях, когда суммарная погрешность оказывается больше допуска на выполняемый размер, т. е. при ω=ω_п+ω_р>δ, метод кривых распределения позволяет определить вероятный процент годных деталей или вероятный процент брака.

Источник