- Аналитические методы отделения корней
- Аналитический метод отделения корней
- 2. Аналитический способ отделения корней
- Вычислительная математика копия 1
- 1.1 Отделение корня
- Графический метод отделения корня
- 1.2 Уточнение корня методом деления отрезка пополам
- 1.3 Метод хорд
- Реферат: Отделение корней. Графический и аналитический методы отделения корней
- Содержание
- 1. Отделение корней. 3
- 2. Графический метод. 4
- 3. Аналитический метод (табличный или шаговый). 5
- 4. Метод половинного деления (Дихотомии). 9
- 1. Отделение корней
- 2. Графический метод
- 3. Аналитический метод (табличный или шаговый).
Аналитические методы отделения корней
Цель работы
Целью работы является изучение численных методов решения алгебраических и трансцендентных уравнений. В настоящей работе рассматриваются следующие методы нахождения корней уравнения :
· — Метод деления отрезка пополам.
· — Метод касательных (Метод Ньютона).
Примеры заданий
Найти корни уравнений :
1. x 2 — 0.5 + sin(x) =0;
2. 2 * sin(x) — x 2 + 0.3 * x = 0;
3. 0.1 * sin(x) + x 3 — 1 = 0;
4. 0.1 * x 2 — x * Ln(x) = 0;
5. 0.1 * x 3 — 2 * x 2 + x — 5 = 0;
6. x 3 — 0.39 * x 2 — 10.5 * x + 11 = 0;
8. 2.5 — 3 * sin(x + Pi / 4) = 0 ;
9. abs(x) + cos(x + Pi / 8) — 2.5 = 0.
Найти минимальный положительный корень :
10. sin(x) = P — q * x, 0 0;
13. Ln(x) = P — q * x 2 , P,q > 0.
Теоретические сведения
Пусть уравнение имеет вид f(x) = 0. Функция f(x) определена в некотором конечном или бесконечном интервале a
6.3.4 Метод деления отрезка пополам
Дана функция f(x) непрерывная на отрезке a,b и удовлетворяющая условию f(a) * f(b) k .
При k ® 


Процесс деления отрезка прекращается при условии, что
Противоположная граница будет неподвижной (точка d). Вычисления корня прекращаются при условии, что
Источник
Аналитический метод отделения корней



Для отделения действительных корней непрерывных функций следует помнить следующее:
ü если функция f(x) непрерывна на интервале [a, b] и имеет на концах интервала [a, b] одинаковые знаки (т.е. f(a)·f(b) > 0), то на этом интервале имеется четное число корней или их нет (рис. 2);
! нельзя забывать, что корнем функции может быть не только точка пересечения графика функции f(x) с осью x, но и его касание с осью x (рис. 3). В этом случае монотонность функции нарушается.
ü если функция f(x) непрерывна на интервале [a, b] и имеет на концах интервала [a, b] разные знаки (т.е. f(a)·f(b)
! иногда для единственности корня бывает достаточно и знакопостоянства второй производной.
Таким образом, чтобы отделить все корни уравнения, следует:
Вычислим значения функции f(x) на концах отрезка [-3, 3]:
f(-3) = (-3) 3 — 8·(-3) + 2 = -1, f(3) = (3) 3 — 8·3 + 2 = 5.
f(-3)∙f(3) 2 — 8 – непрерывна. Для определения интервалов монотонности f(x) найдем значения x, при которых f’(x) = 0. f’(x) = 3x 2 – 8 = 0 при x = 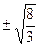
Таким образом, можно отделить следующие интервалы монотонности функции f(x): [-3; -1,633], [-1,633; 1,633], [1,633; 3] и на каждом из этих интервалов отделено по одному корню уравнения.
Для наглядности вычислим значения f(x) и f’(x) на концах этих промежутков (табл. 1). f’(x) = 3x 2 – 8.
Источник
2. Аналитический способ отделения корней
Аналитический способ отделения корней основан на следующей теореме:
» Если функция F(x), определяющая уравнение F(x)=0, на концах отрезка [a;b] принимает значения разных знаков, т.е. F(a)*F(b) 0 (4)) .
Для отделения корней аналитическим способом выбирается отрезок [A;B], на котором находятся все интересующие вычислителя корни уравнения. Причем на отрезке [A;B] функция F(x) определена, непрерывна и F(a)*F(b) 0;»корень на данном отрезке единственный»;»Корень не единственный»).
В результате получаем:
Таким образом доказано существование и единственность корня на отрезке изоляции.
отделить корни уравнения cos(2x)+x-5=0 аналитическим способом с шагом 1 на отрезке [-10;10], используя:
Чтобы отделить корни уравнения аналитическим способом с помощью MS Excel, необходимо выполнить следующее:
Заполнить ячейки A1:D1 соответственно: «x», «y=cos(2x)+x-5», «h», «ответ».
В С2 ввести значение 1.
Ввести в А2 значение -10.
Ввести в А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.
В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.
В D3 ввести формулу =ЕСЛИ(B2*B3 2 / 5 2 3 4 5 > Следующая > >>
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Вычислительная математика копия 1
Уравнение называется алгебраическим, если его можно представить в виде:
Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение f(x)=0 не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.
Решить уравнение означает найти такие значения x , при которых уравнение превращается в тождество.
Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n =1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n >4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.
1.1 Отделение корня
Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.
Отделить корень – значит указать такой отрезок [a , b] , на котором содержится ровно один корень уравнения f(x)=0.
Не существует алгоритмов отделения корня, пригодных для любых функций f (x). Если удастся подобрать такие a и b , что
2) f ( x ) – непрерывная на [ a , b ] функция (1.3)
3) f ( x ) – монотонная на [ a , b ] функция (1.4)
то можно утверждать, что на отрезке [a , b] корень отделен.
Условия (1.2) –(1.4) – достаточные условия того, что корень на [a , b] отделен, то есть если эти условия выполняются, то корень отделен, но невыполнение, например, условий (1.3) или (1.4) не всегда означает, что корень не отделен.
Корень можно отделить аналитически и графически.
Пример. Аналитически отделить положительный корень уравнения x 3 -7x-5=0 Решение. Составим таблицу
Графический метод отделения корня
1.2 Уточнение корня методом деления отрезка пополам
Уточнить корень – значит найти его приближенное значение с заданной погрешностью e .
Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.
Предположим, что отрезок [a , b], на котором отделен корень уравнения, уже найден.
Пусть, например, f(a)> 0, f(b) e 1=(b-a)/2. Если эта погрешность не превышает некоторую заданную погрешность e , с которой нужно уточнить корень уравнения, то вычисления прекращаем и можно записать: ?=x ±(b-a)/2 . В противном случае определяем новый отрезок [a , b], на котором отделен корень нашего уравнения. Для этого определим знак функции в точке х. В нашем примере f (x )>0. Новый отрезок – отрезок [x , b], так как на концах этого отрезка функция имеет разные знаки. Переобозначим один из концов отрезка – в нашем случае положим a = x — и повторим процедуру для нового отрезка [a , b].
1.3 Метод хорд
Идея метода состоит в следующем. Проводим прямую через точки с координатами (a ,f(a)), (b ,f(b)). Находим точку пересечения прямой с осью Х. Определяем знак функции в этой точке. Далее проводим прямую через те точки, абсциссы которых содержат корень уравнения ? . Вычисления прекращаются, как только выполнится условие |xn+1-xn| e .
Источник
Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
3. Аналитический метод (табличный или шаговый).
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
Источник







 Министерство образования и науки РФ
Министерство образования и науки РФ 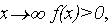 при
при 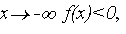 что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.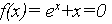 видим, что
видим, что 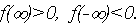 Обнаружив, что
Обнаружив, что 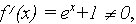 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).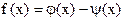 и строить графики функций
и строить графики функций 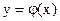 и
и 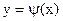 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.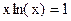 .
.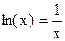 , т.е.
, т.е. 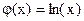 и
и 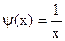 .
.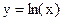 и
и 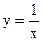 .
.