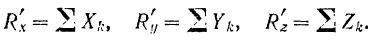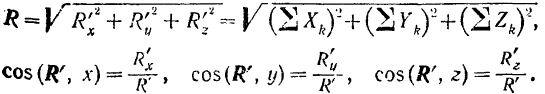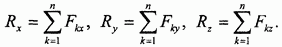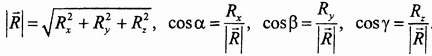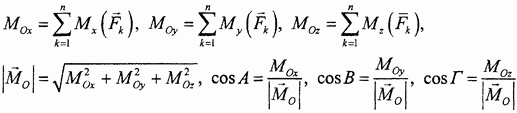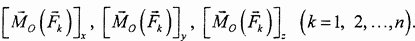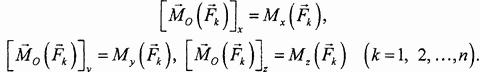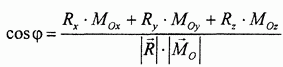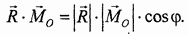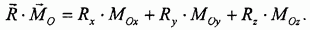Аналитический способ определения главного вектора

11 Вычисление главного вектора и главного момента

Для плоской билет В аналитическом методе для вычисления главного вектора и главного момента используются проекции сил F_ix, F_iy и координаты x_i, y_i точек их приложения.

Модуль R главного вектора плоской системы сил и его направляющие косинусы e_x, e_у вычисляются по следующим формулам:

R = (R_х + R_y) ; e_x = R_x / R; e_y = R_у / R; R_x = F_ix; R_y = F_iy.

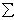
Здесь в суммировании проекций можно не включать силы, образующие пары сил (F_k, F‘_k), F_k = —F‘_k, поскольку суммы проекций таких двух сил на любую ось равны нулю.

Алгебраический главный момент L_O плоской системы сил относительно центра O ( начала координатных осей ) вычисляется по формуле:

L_O = (x_i F_iy — y_i F_ix) + M_k.

Здесь во вторую сумму выделены алгебраические моменты M_k пар сил (F_k, F‘_k).

В случаях, когда плечи h_i всех сил определяются достатосно просто ( например, если силы параллельны координатным осям Ox и Oy ), величина L_O может быть вычислена по формуле:

L_O = 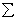± F_i h_i + M_k.

,а для пространства

Главный вектор и главный момент пространственной системы сил

В аналитическом методе для вычисления главного вектора и главного момента используются проекции сил F_ix, F_iy, F_iz и координаты x_i, y_i, z_i точек их приложения.

Модуль R главного вектора системы сил и его направляющие косинусы e_x, e_у, e_z вычисляются по следующим формулам:

R = (R_х + R_y + R_z) 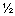; e_x = R_x / R; e_y = R_у / R; e_z = R_z / R;

R_x = F_ix; R_y = F_iy; R_z = F_iz.

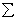
Здесь в суммировании проекций можно не включать силы, образующие пары сил (F_k, F‘_k), F_k = —F‘_k, поскольку суммы проекций таких двух сил на любую ось равны нулю.

Модуль главного момента L_O системы сил относительно центра O (начала координатных осей) и его направляющие косинусы l_x, l_у, l_z вычисляются по формулам:

L_O = (L_Oх + L_Oy + L_Oz) ; l_x = L_Ox / L_O; l_y = L_Oу / L_O; l_z = L_Oz / L_O;

L_Ox = (y_i F_iz — z_i F_iy) + M_kx. L_Oy = (z_i F_ix — x_i F_iz) + M_ky. L_Oz = (x_i F_iy — y_i F_ix) + M_kz.

Здесь во вторую сумму выделены векторные моменты M_k пар сил (F_k, F‘_k).

В случаях, когда плечи сил определяются достатосно просто (например, если силы параллельны координатным осям Ox,Oy,Oz), осевые моменты таких сил при вычислении проекций L_Ox, L_Oy, L_Oz можно определять геометрическим методом.

Геометрический метод: момент силы относительно оси равен алгебраическому моментупроекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Алгебраическим моментом силы относительно точки называют взятое с соответствующим знаком произведение модуля силы на плечо силы относительно этой точки.

Плечом силы относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, то есть длину отрезка перпендикуляра, опущенного из точки на линию действия силы.

Mомент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси, стремится вращать тело против хода часовой стрелки, глядя с положительного направления оси.

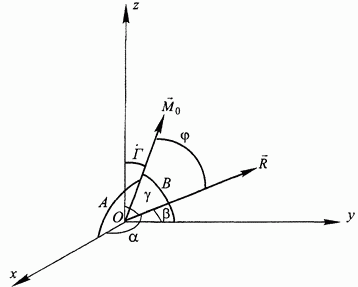
Например момент силы F (см.рис.) относительно оси Oz равен произведению модуля ее проекции F_xy на плоскость Oxy на плечо h этой проекции относительно точки О, взятое со знаком плюс: M_Oz = + F_xy h.

Момент силы относительно оси равен нулю (M_Oz = 0), если:

сила параллельна оси (в этом случае равен нулю модуль проекции силы на плоскость, перпендикулярную оси: F_xy = 0);

линия действия силы пересекает ось (в этом случае линия действия проекции силы на плоскость, перпендикулярную оси, также пересекает эту ось и плечо этой проекции равно нулю: h = 0).

Объединяя эти два случая, можно сказать: момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

12 Центр тяжести дуги, окружности треугольника, кругового сектора Дуга окружности: центр тяжести дуги однородной окружности находится на оси симметрии (координата уc=0).

где α – половина центрального угла; R – радиус окружности.

Однородный круговой сектор: центр тяжести расположен на оси симметрии (координатауc=0).

где α – половина центрального угла; R – радиус окружности.

Треугольник: центр тяжести однородного треугольника находится в точке пересечения его медиан.

где x1, y1, x2, y2, x3, y3 – координаты вершин треугольника

Источник

Аналитический способ определения главного вектора

Аналитический способ определения главного вектора

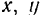
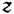
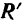
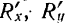
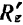
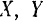
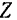
Согласно известной из векторной алгебры теоремы: проекция геометрической суммы векторов (их главного вектора) на какую-либо ось равна алгебраической сумме проекций составляющих векторов на ту же ось. Отсюда, обозначая проекции на координатные оси и главного вектора данной системы сил через и , а проекции составляющих сил на те же оси, как это часто принято, заглавными буквами и с соответствующими индексами, будем иметь:

Модуль и направление главного вектора, а следовательно, и равнодействующей системы сходящихся сил, очевидно, можно определить, воспользовавшись формулами (4) и (5):

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Вычисление и построение главного вектора и главного момента

Выбираем систему координатных осей Oxyz (рис. 48) и вычисляем проекции главного вектора как алгебраические суммы проекций всех заданных сил на выбранные оси:

По найденным проекциям, откладывая соответствующие отрезки вдоль координатных осей (с учетом знака проекции), строим прямоугольный параллелепипед. Направленная диагональ, проведенная из начала координат в противоположную вершину параллелепипеда, определяет главный вектор R (см. также рис. 26).

Модуль и направляющие косинусы главного вектора определяются следующими вытекающими из построения формулами:

Совершенно аналогично определяются проекции, модуль и направляющие косинусы главного момента:

К формулам для вычисления проекций главного момента необходимо привести следующие пояснения.

Главный момент, по определению, есть векторная сумма моментов всех сил центра О. Следовательно, его проекции на координатные оси равны алгебраическим суммам проекций на эти оси векторов-моментов сил относительно центра О, то есть величин

Но эти величины, по определению момента силы относительно оси, являются моментами сил относительно соответствующих координатных осей:

Отсюда непосредственно следуют написанные выше выражения для величин .

Косинус угла 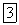между главным вектором и главным моментом определяется так:

Формула получается следующим образом. По определению скалярного произведения векторов R и имеем:

С другой стороны, эта же величина может быть вычислена через проекции векторов-сомножителей:

Приравнивая правые части и разрешая полученное уравнение относительно coscp, приходим к написанной формуле.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник