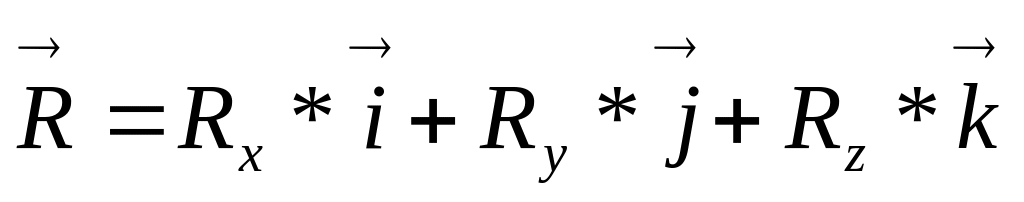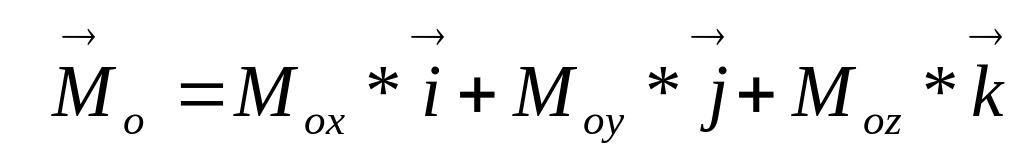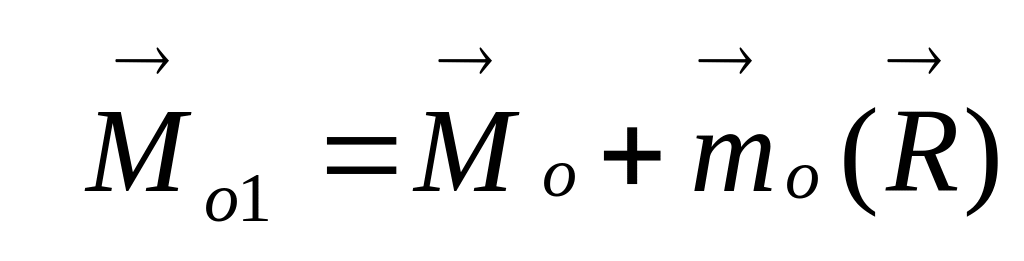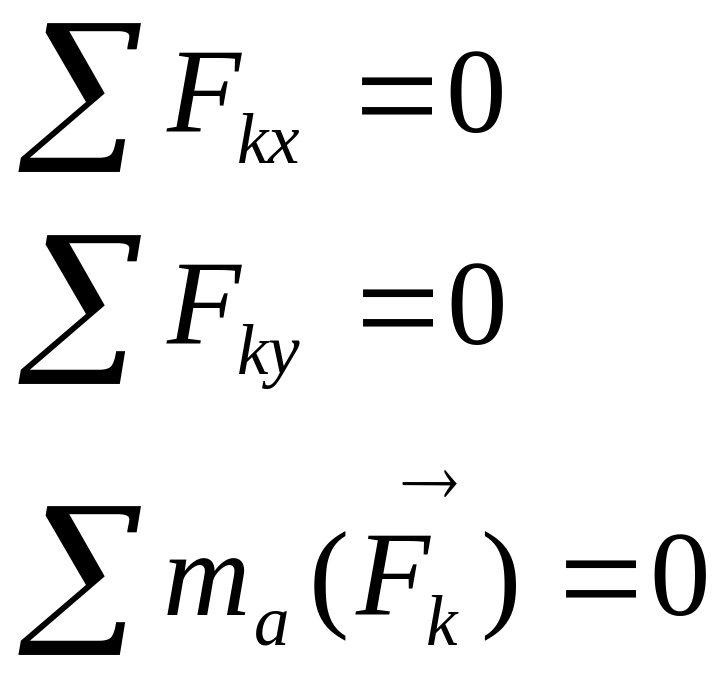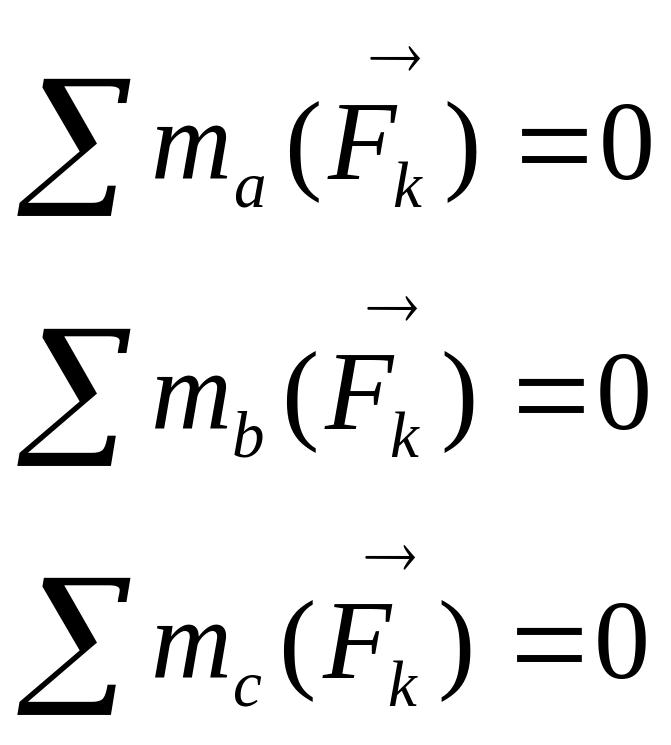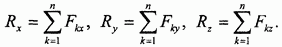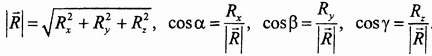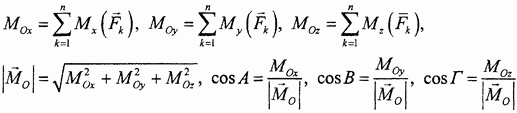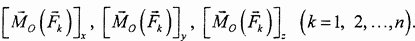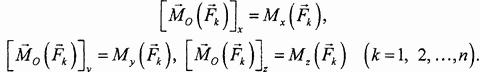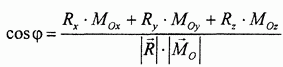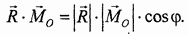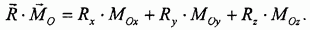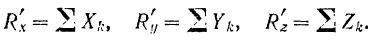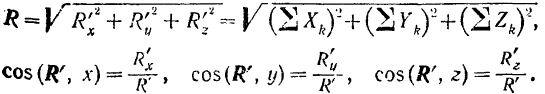Аналитический способ определения главного момента

В основе способа лежит известное из векторной алгебры представление векторного произведения в виде определителя, что позволяет записать для вектора-момента силы следующее выражение

Здесь — орты координатных осей; , у, z- координаты точки приложения силы; проекции силы на координатные оси. Вспоминая, что в формуле разложения вектора на составляющие по координатному базису коэффициенты при ортах являются проекциями этого вектора на соответствующие оси, а в данном случае, по определению — моментами силы F относительно координатных осей, приходим к равенствам:

Полученные формулы называются аналитическими выражениями для моментов силы относительно координатных осей. Они позволяют вычислять моменты силы относительно координатных осей без предварительного построения момента относительно начала координат.

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Источник

XIV Аналитическое определение главного моменты вектора и главного момента.

Направление главного вектора системы сил определяется направляющими косинусами(cos угла между равнодействующей и единичными векторами)

XV Изменение главного момента при переносе центра приведения.

Главный момент относительно нового центра приведения равен геометрической сумме главного момента относительно старого центра приведения и вектора момента главного вектора системы относительно нового центра приведения.

XVI Момент силы относительно оси через момент силы относительно точки на этой оси.

Момент силы относительно оси равен проекции на эту ось вектора момента относительно точки, лежащей на этой оси.

XVII Условие равновесия произвольной пространственной системы сил.

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы сумма проекций всех сил системы на оси координат и суммы моментов всех сил системы относительно осей координат равнялись нулю.

XVIII Условие равновесия системы параллельных сил в пространстве.

Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил системы на параллельную ось равнялась нулю, а так же сумма моментов всех сил системы на другие оси равнялась нулю.

Задача считается статически разрешимой, если количеству неизвестных равно количество составленных уравнений.

XIX Условие равновесия плоской системы сил.

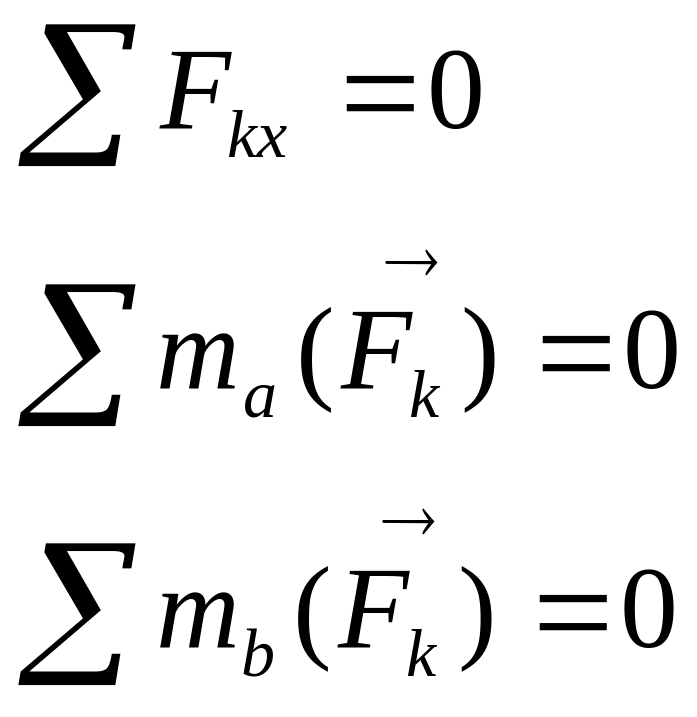
только при не перпендикулярности оси Х и тела

3) третья форма через моменты трех точек, не лежащих на одной прямой

XXII Теорема Вариньона. (О моменте равнодействующей) плоской и пространственной системы сил.

Если произвольная пространственная система сил приводится к равнодействующей, то ее момент относительно любого центра равен векторной сумме моментов всех сил системы относительно того же центра.

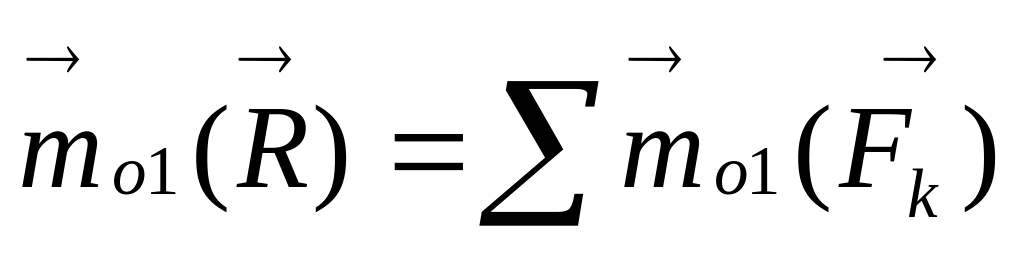
это уравнение можно проецировать на любую ось

Если произвольная плоская система сил приводится к равнодействующей, то момент равнодействующей системы сил относительно любого центра равен алгебраической сумме моментов всех сил системы относительно того же центра.

XXIII Статически определимые и неопределимые задачи.

Если количество неизвестных в уравнениях соответствует количеству неизвестных, то такая задача является статически определимой. Если же наоборот, то с помощью уравнений такую задачу решить невозможно.

XXIV Трение скольжения.

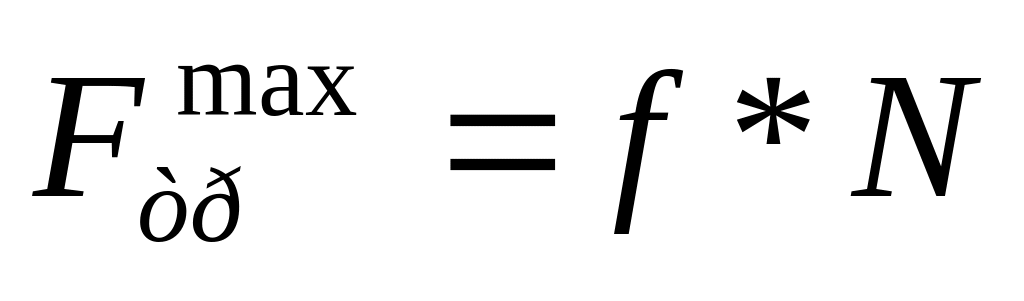
, где f – коэффициент трения, N – нормальная реакция(сила реакции опоры)

Коэффициент зависит от: температуры, материала, влажности, но не зависит от площади соприкосновения.

Равнодействующая сила, от сил трения и нормальной реакции, образует конус трения, угол 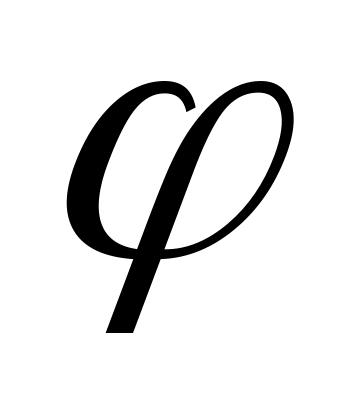, который образуется между равнодействующей и нормальной реакцией.

tg 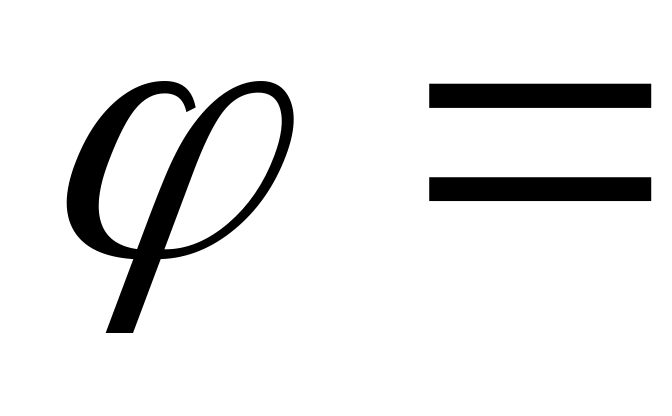f – коэффициенту трения.

Никакая сила лежащая внутри конуса трения не выведет тело из состояния равновесия.

XXV Трение качения.

Трение, возникающие при качении одного тела по поверхности другого.

f_k – коэффициент трения качения

Физический смысл коэффициента – смещение нормальной реакции по отношению к линии действия силы тяжести.

, где r – радиус колеса

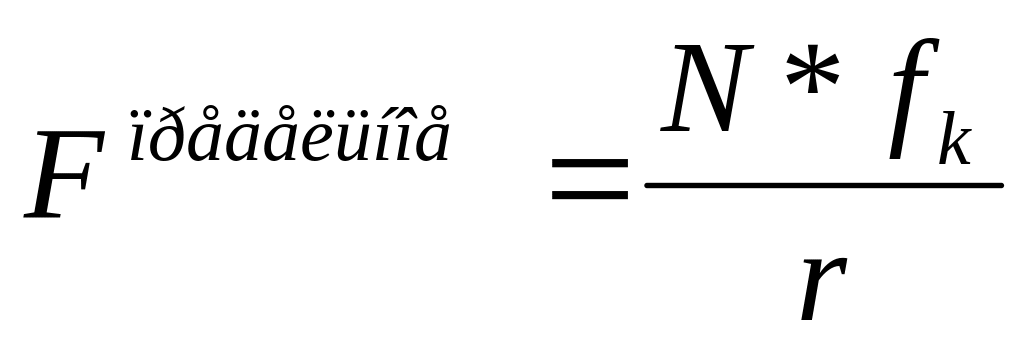
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Вычисление и построение главного вектора и главного момента

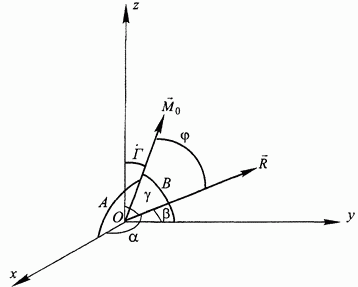
Выбираем систему координатных осей Oxyz (рис. 48) и вычисляем проекции главного вектора как алгебраические суммы проекций всех заданных сил на выбранные оси:

По найденным проекциям, откладывая соответствующие отрезки вдоль координатных осей (с учетом знака проекции), строим прямоугольный параллелепипед. Направленная диагональ, проведенная из начала координат в противоположную вершину параллелепипеда, определяет главный вектор R (см. также рис. 26).

Модуль и направляющие косинусы главного вектора определяются следующими вытекающими из построения формулами:

Совершенно аналогично определяются проекции, модуль и направляющие косинусы главного момента:

К формулам для вычисления проекций главного момента необходимо привести следующие пояснения.

Главный момент, по определению, есть векторная сумма моментов всех сил центра О. Следовательно, его проекции на координатные оси равны алгебраическим суммам проекций на эти оси векторов-моментов сил относительно центра О, то есть величин

Но эти величины, по определению момента силы относительно оси, являются моментами сил относительно соответствующих координатных осей:

Отсюда непосредственно следуют написанные выше выражения для величин .

Косинус угла 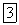между главным вектором и главным моментом определяется так:

Формула получается следующим образом. По определению скалярного произведения векторов R и имеем:

С другой стороны, эта же величина может быть вычислена через проекции векторов-сомножителей:

Приравнивая правые части и разрешая полученное уравнение относительно coscp, приходим к написанной формуле.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Аналитический способ определения главного вектора

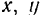
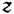
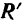
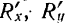
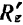
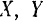
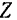
Согласно известной из векторной алгебры теоремы: проекция геометрической суммы векторов (их главного вектора) на какую-либо ось равна алгебраической сумме проекций составляющих векторов на ту же ось. Отсюда, обозначая проекции на координатные оси и главного вектора данной системы сил через и , а проекции составляющих сил на те же оси, как это часто принято, заглавными буквами и с соответствующими индексами, будем иметь:

Модуль и направление главного вектора, а следовательно, и равнодействующей системы сходящихся сил, очевидно, можно определить, воспользовавшись формулами (4) и (5):

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Источник