Аналитический способ описания равномерного движения

Способы описания прямолинейного движения

Простейшим видом движения точечного тела является движение вдоль прямой. Такое движение называют прямолинейным.

Рассмотрим достаточно простой пример прямолинейного движения. Представим себе, что на столе лежит ученическая линейка. В том месте, где у линейки находится нулевая отметка, лежит крупинка сахара. Муравей, схватив крупинку сахара в тот момент, когда мы включили секундомер, начинает бежать вдоль края линейки в сторону увеличения значений ее сантиметровых делений (рис. 7, а).

Перед нами стоит задача: описать механическое движение этого муравья. Поскольку механическое движение по определению есть изменение положения тела относительно другого тела с течением времени, то для описания изменения положения муравья мы должны выбрать тело отсчета и связать с ним координатную ось. Пусть таким телом будет стол. За начало отсчета примем точку, в которой муравей взял крупинку сахара (нулевое деление на линейке). Ось координат X направим параллельно краю линейки в сторону движения муравья. За единицу длины выберем 1 см. Для отсчета времени будем использовать секундомер.

В результате мы получили то, что называют системой отсчета. В этой системе отсчета муравей движется вдоль прямой линии — края линейки, т. е. мы имеем дело с прямолинейным движением.
Включим секундомер в момент старта муравья и будем фиксировать по линейке координаты муравья xм в разные моменты времени, изображенные на рис. 7. Используя эти данные, составим таблицу.

В первой строке таблицы приведены значения моментов времени, в которые нам известны положения муравья относительно начала отсчета. Во второй строке приведены соответствующие им координаты муравья.

Такой способ описания механического движения носит название табличного. Ясно, что чем больше указано в таблице моментов времени, тем точнее описано движение тела. Например, в нашем случае, глядя на таблицу, можно только предполагать, где находился муравей, когда секундомер показывал t = 2 с или t = 6 с.

Табличный метод является достаточно простым и наглядным. Поэтому он часто используется на практике. Например, если вы посмотрите на расписание движения электропоездов по станциям или рейсовых автобусов по остановкам, то поймете, что это и есть табличный способ описания движения этих тел.

Наряду с табличным способом задания зависимости одной величины от другой часто используют графический способ. В нашем случае для построения графика зависимости координаты муравья от времени, в течение которого он двигался, мы должны построить прямоугольную систему координат, в которой начало координат будет началом отсчета и времени, и координаты движущегося тела. Пусть при этом ось абсцисс будет осью времени t, а ось ординат — осью координат X.

Из математики известно, что любая точка в прямоугольной системе координат задается упорядоченной парой чисел, которые называют координатами точки. Первое число задает координату точки по оси абсцисс, второе — по оси ординат. Таким образом, положение движущегося вдоль оси X тела в определенный момент времени надо задавать парой чисел: моментом времени t на оси времени (ось абсцисс) и соответствующим ему значением координаты x на оси координат (ось ординат).

Нанесем на оси единицы величины: по оси времени — секунда (с), по оси координат — сантиметр (см). Для построения графика движения следует перенести данные из таблицы на координатную плоскость.

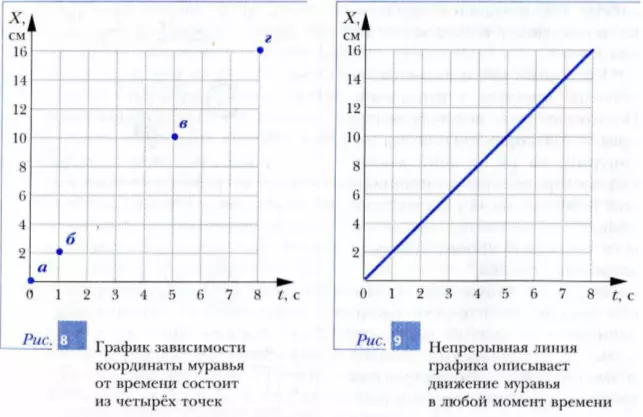
Поскольку мы знаем координаты муравья только в четыре момента времени (t = 0, 1, 5 и 8 с), то график будет состоять только из четырех точек (рис. 8). Ясно, что если бы нам было известно, где находился муравей в другие моменты времени (например, в моменты t = 2, 3, 4, 6 с и т. д.), то точек на графике было бы больше. В идеальном случае, если бы нам были известны координаты муравья в любой момент времени его движения, наш график превратился бы в некоторую линию (например, в прямую, как на рис. 9). При этом мы получили бы описание движения тела для любого момента времени.

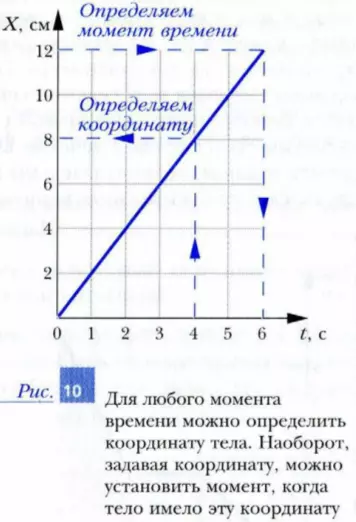
Посмотрим, как можно воспользоваться таким графиком. Для этого обратимся к рис. 10, на котором изображен график движения муравья. Пусть нам нужно определить, где находится муравей в тот момент, когда секундомер показывал время t = 4 с. Для этого найдем на оси времени точку с координатой t = 4 с и проведем вертикальную пунктирную линию до пересечения с графиком движения. От полученной точки проведем горизонтальную пунктирную линию до пересечения с осью X координат муравья. Легко видеть, что это точка на оси X имеет координату x_м = 8 см.

Можно решить и обратную задачу: задать координату муравья и определить, в какой момент времени он находился в выбранной точке пространства. В этом случае, отмечая на оси X точку с выбранной нами координатой, например x_м = 12 см, мы должны провести через нее горизонтальную линию до пересечения с графиком движения. Далее от точки пересечения следует провести вертикальную линию вниз и найти интересующее нас значение времени: t = 6 с.

Таким образом, мы убедились, что если график движения тела представляет собой непрерывную линию, то мы можем ответить на оба вопроса механики — где и когда находилось, находится или будет находиться тело. В этом случае говорят, что движение тела описано полностью.

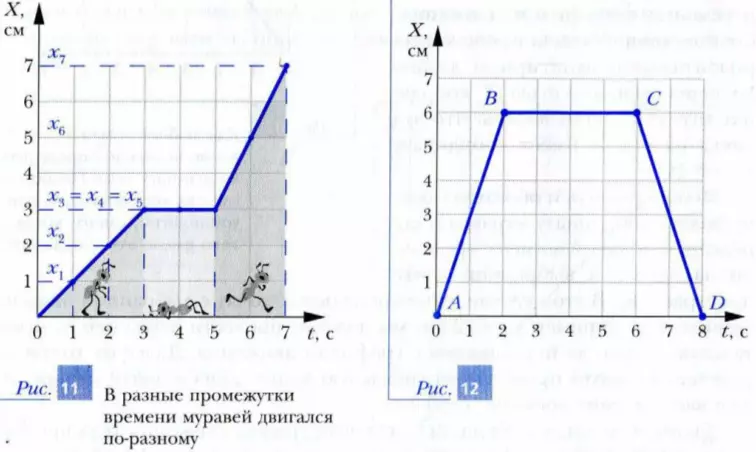
Разобранный нами пример графического способа описания механического движения часто используют на практике. Для иллюстрации сказанного рассмотрим движение муравья, используя график, приведенный на рис. 11.

Из данного графика видно, что в течение первых трех секунд координата муравья непрерывно увеличивалась. Следовательно, он двигался в положительном направлении оси X. Кроме того, за каждую из первых трех секунд он увеличивал свою координату на 1 см. Далее мы видим, что с момента t₃ = 3 с до момента t₅ = 5 с координата муравья оставалась равной x₃ = 3 см. Это означает, что положение муравья в выбранной системе отсчета не изменялось. Проще говоря, муравей не двигался. По-видимому, он устал и отдыхал. Начиная с момента времени t₅ = 5 с координата муравья опять изменялась. За шестую секунду она увеличилась от x₅ = 3 см до x₆ = 5 см, т. е. на два сантиметра. На ту же самую величину увеличилась координата муравья и за седьмую секунду движения. Значит, отдохнув, муравей в течение шестой и седьмой секунд двигался быстрее, чем до отдыха. Отметим, что, так как в течение шестой и седьмой секунд движения координата муравья увеличивалась, мы можем сделать вывод, что муравей опять двигался в положительном направлении оси X.

Вы, наверное, уже догадались, что, если на каком-либо графике, описывающем движение тела, координата тела с течением времени уменьшается, это означает, что тело движется в отрицательном направлении оси X.

Итоги

Прямолинейное движение тела — это движение, при котором тело движется по прямой линии в данной системе отсчета.

Чтобы описать прямолинейное движение в выбранной системе отсчета, необходимо в момент начала движения включить часы и измерять координату тела в различные моменты времени.

Результаты измерений представляют в виде таблицы (табличный способ описания движения) или графика движения в осях: время — координата (графический способ описания движения).

Если известна графическая зависимость координаты тела от времени в виде непрерывной линии, то движение тела описано полностью, т. е. можно:

Определить координату тела в любой момент времени движения (ответить на вопрос «где?»).
Определить момент времени, в который тело имело заданную координату (ответить на вопрос «когда?»).
Охарактеризовать движение тела (указать, покоилось ли тело, двигалось ли в положительном или отрицательном направлении координатной оси, как быстро изменялась его координата с течением времени).

Источник

Аналитический способ описания равномерного движения

В кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси.

1. Векторный способ.

В этом способе положение материальной точки `A` задаётся с помощью так называемого радиус-вектора `vecr`, который представляет собой вектор, проведённый из точки `O`, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку `A` (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени `vecr=vecr(t)`.

Геометрическое место концов радиус-вектора `vecr(t)` называют траекторией точки `A`.

В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка `A` после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.

Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени `Delta t` тело (точка `A`) переместилось из начального положения `1` с радиус-вектором `vec r_1` в конечное положение `2` с радиус-вектором `vec r_2` (рис. 2). Приращение `Deltavec r` радиус-вектора тела в таком случае равно: `Deltavec r = vec r_2- vec r_1`.

Вектор `Deltavec r`, соединяющий начальное и конечное положения тела, называют перемещением тела.

Отношение `Delta vec r//Delta t` называют средней скоростью (средним вектором скорости) `vec v_»cp»` тела за время `Delta t`:

`vecv_»cp»=(Deltavecr)/(Delta t)` (1)

Вектор `vecv_»cp»` коллинеарен и сонаправлен с вектором `Deltavec r`, так как отличается от последнего лишь скалярным неотрицательным множителем `1//Delta t`.

Предложенное определение средней скорости справедливо для любых значений `Delta t`, кроме `Delta t=0`. Однако ничто не мешает брать промежуток времени `Delta t` сколь угодно малым, но отличным от нуля.
Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени `t` или в конкретной точке траектории. С этой целью промежуток времени `Delta t` устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение `Delta vec r`. При этом отношение `Deltavec r//Delta t` стремится к определённому значению, не зависящему от `Delta t`.

Величина, к которой стремится отношение `Deltavec r//Delta t` при стремлении `Delta t` к нулю, называется мгновенной скоростью`vec v`:

`vec v =(Delta vec r)/(Delta t)` при `Delta t -> 0`.

Теперь заметим, что чем меньше `Delta t`, тем ближе направление `Deltavec r` к направлению касательной к траектории в данной точке. Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела.

В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости `vec v` тела (материальной точки).

Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения. Его определяют через отношение приращения вектора скорости `Delta vec v` тела к промежутку времени `Delta t`, в течение которого это приращение произошло.

Ускорением `veca` тела называется величина, к которой стремится отношение `Delta vec v//Delta t` при стремлении к нулю знаменателя `Delta t`:

`vec a =(Delta vec v)/(Delta t)` при `Delta t -> 0` (2)

При уменьшении `Delta t` ориентация вектора`Delta vec v` будет приближаться к определённому направлению, которое принимается за направление вектора ускорения `vec a`. Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости!

Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (`»м»//»с»`) и метр на секунду в квадрате ( `»м»//»с»^2`).

2. Координатный способ.

В этом способе положение материальной точки `A` на плоскости в произвольный момент времени `t` определяется двумя координатами `x` и `y`, которые представляют собой проекции радиус-вектора $$ \overrightarrow$$тела на оси `Ox` и `Oy` соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями `t`: $$ x=x\left(t\right)$$ и $$ y=y\left(t\right)$$. Если эти функции известны, то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости $$ \overrightarrow$$ можно спроецировать на оси координат и определить таким образом скорости $$ _$$ и $$ _$$ изменения координат тела (рис. 4). В самом деле $$ _$$ и $$ _$$ будут равны значениям, к которым стремятся соответственно отношения `Delta x//Delta t` и `Delta y//Delta t` при стремлении к нулю промежутка времени `Delta t`.

3. Естественный (или траекторный) способ.

Этот способ применяют тогда, когда траектория материальной точки известна заранее. На заданной траектории `LM` (рис. 5) выбирают начало отсчёта – неподвижную точку `O`, а положение движущейся материальной точки `A` определяют при помощи так называемой дуговой координаты `l`, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта `O` до точки `A`. При этом положительное направление отсчёта координаты `l` выбирают произвольно, по соображениям удобства, например так, как показано стрелкой на рис. 5.

Движение тела определено, если известны его траектория, начало отсчёта `O`, положительное направление отсчёта дуговой координаты `l` и зависимость $$ l\left(t\right)$$.

Следующие два важных механических понятия – это пройденный путь и средняя путевая скорость.
По определению, путь `Delta S` — это длина участка траектории, пройденного телом за промежуток времени `Delta t`.

Ясно, что пройденный путь – величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением `Delta vec r`, представляющим собой вектор. Сравнивать можно только путь `Delta S` и модуль перемещения `
|Delta vecr|`. Очевидно, что `Delta S >=|Deltavec r|`.

Средней путевой скоростью `v_»cp»` тела называют отношение пути `Delta S` к промежутку времени `Delta t`, в течение которого этот путь был пройден:

`v_»cp»=(Delta S)/(Delta t)` (3)

Определённая ранее средняя скорость `v_»cp»` (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как `Deltavec r` отличается от `Delta S`, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения `Delta t`. Само слово «средняя» означает усреднение по времени.

Городской троллейбус утром вышел на маршрут, а через 8часов, проехав в общей сложности `72` км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость `vec v_»cp»` и средняя путевая скорость `v_»cp»` троллейбуса?

Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение `Delta vecr` равно нулю: `Deltavecr=0`, следовательно, `vecv_»ср»=Deltavecr//Deltat=0` и `|vecv_»ср»|=0`. Но средняя путевая скорость троллейбуса не равна нулю:

`v_»cp»=(Delta S)/(Delta t)=(72 «км»)/(8 «ч»)=9 «км»//»ч»`.

Источник