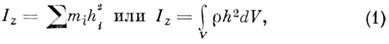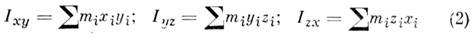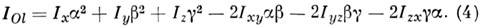Определение центра тяжести плоской фигуры
методическая разработка
Определение центра тяжести плоской фигуры. В разработке указан способ определения центра тяжести аналитическим образом. Разработка будет полезна студентам для осовения практических умений по дисциплине «Техническая механика».
Скачать:
| Вложение | Размер |
|---|---|
| metodicheskaya_razrabotka_tsentr_tyazhesti_ploskoy_figury.docx | 165.39 КБ |
Предварительный просмотр:
Определение центра тяжести плоской фигуры
Центр тяжести применяется при исследовании устойчивости положений равновесия тел и сплошных сред, находящихся под действием сил тяжести и в некоторых других случаях, а именно: в сопротивлении материалов и в строительной механике – при использовании правила Верещагина.
При определении координат центра тяжести используются следующие методы:
1) метод симметрии: если сечение имеет центр симметрии или ось симметрии, то центр тяжести находится в центре симметрии или на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых, легко определить;
3) метод отрицательных площадей: этот способ является частным случаем способа разделения. Он используется, когда сечение имеет вырезы, срезы, полости (отверстия), которые рассматриваются как часть сечения с отрицательной площадью.
При решении задач на определение центра тяжести сложных сечений следует придерживаться следующего порядка:
1. Выбрать метод, который наиболее применим к данной задаче.
2. Разбить сложное сечение на простые части, для которых центры тяжести известны.
3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии.
4. Определить координаты центров тяжести отдельных частей относительно выбранных осей.
5. Используя формулы определить искомые координаты центра тяжести заданного сечения.

где А 1 , А 2 . Аn — площади простых сечений;
x 1 , x 2 … x n , y 1 , y 2 … y n – координаты центра тяжести простых сечений.
Координаты центра тяжести сложной плоской фигуры определяются после разделения ее на простые фигуры и определения их центров тяжести.
Координаты центра тяжести некоторых простых плоских фигур:
Порядок выполнения задания:
1) начертить заданное сложное сечение (фигуру), выбрать оси координат.
2) разбить сложное сечение на простые, для которых центры тяжести и силы тяжести известны;
3) определить необходимые данные для простых сечений:
4) определить координаты центров тяжести простых сечений относительно выбранных осей координат;
5) определить положение центра тяжести сложного сечения.
Найти координаты центра тяжести плоской фигуры, изображенной на рисунке.
Выбираем оси координат так, чтобы нижний и левый край фигуры совпали с ними:
Делим заданную плоскую фигуру на прямоугольник (1), треугольник (2) и круг (3).
Вычисляем площади этих фигур:
S 1 = 10·20 = 200; S 2 = 0,5·5·10 = 25; S 3 = π·9 =28,3.
Определяем координаты центров тяжести фигур:
x 2 = 5; y 2 = 11,7.
Координаты центра тяжести всей плоской фигуры:
По теме: методические разработки, презентации и конспекты
Проецирование плоских фигур
Методическая разработка по теме Проецирование плоских фигурпо дисциплине инженерная графика. Краткое содержание материала, тестовое задание по теме, задание на графическую работу.
Методическая разработка «Сценарий интегрированного занятия Математика + Информатика «Вычисление площади плоской фигуры с помощью определенного интеграла»
Интегрированный урок — это учебное занятие, на котором тема рассматривается с различных точек зрения, средствами нескольких дисциплин. Интегрированные уроки формируют познавательный интерес обучающихс.
Методическая разработка урока по технической механике «Определение центра тяжести плоской фигуры»
Данная методическая разработка содержит методические указания по проведению лабораторной работы «Определение центра тяжести плоской фигуры».
План — конспект урока на тему Центр тяжести для студентов СПО
ГБПОУ «Навашинский политехнический техникум», Россия, Глебова Ю.В., 2012 г., 12 стр., 76 слайдов; Описание: План-конспект урока по дисциплине «Техническая механика» на тему «Центр тяжести» для студент.
Творческая работа студента «Роль центра тяжести в машиностроении»
ГБПОУ «Навашинский судомеханический техникум»; Выполнил: Кирилов А.В. студент II курса; Руководитель: Глебова Ю.В.,преподаватель ; Исследовательская работа — 26 стр., , 2014 г. Практ.
Методические указания по выполнению лабораторной работы «Определение положения центра тяжести сечения» по дисциплине «Техническая механика»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИГосударственное бюджетное профессиональное образовательное учреждение «Кстовский нефтяной техникум имени Бориса Ивановича Корнилова»ОП-04Система.
Определение центра тяжести плоских фигур
решени задач на определение центра тяжести плоских фигур.
Источник
Методы нахождения центра тяжести
Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:
· метод симметрии;
· метод разбиения;
· метод отрицательных масс.
Рассмотрим приемы, применяемые в каждом из перечисленных методов.
Метод симметрии
Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1).
В этом случае каждой элементарной частице силой тяжести Giс абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a, тогда:
Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
Аналогично можно доказать и следующие положения:
· Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
· Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
· Центр тяжести однородного тела вращения лежит на оси вращения.
Метод разбиения
Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.
Допустим, что мы разбили тело силой тяжести G на три части G’, G», G»’, абсциссы центров тяжести этих частейx’C, x»C, x»’C известны.
Формула для определения абсциссы центра тяжести всего тела:
Перепишем ее в следующем виде:
Последнее равенство запишем для каждой из трех частей тела отдельно:
Сложив левые и правые части этих трех равенств, получим:
Но правая часть последнего равенства представляет собой произведение GxC, так как
Следовательно, xC = (G’x’C + G»x»C + G»’x»’C)/G, что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z:
Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц Gi, а силы тяжести конечных частей; под координатами xi, yi, zi понимают координаты центров тяжести частей, на которые разбито тело.
Метод отрицательных масс
Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.
Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.
Практические методы определения центра тяжести тел
На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания, который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.
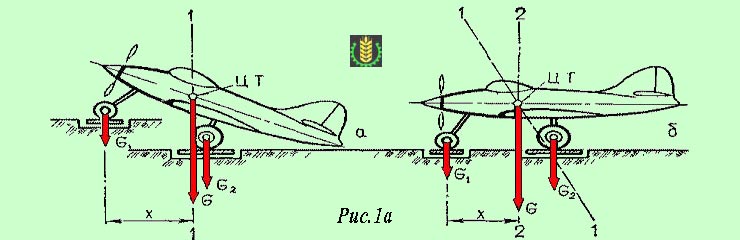
Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания. Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.
Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а).
Вопрос 12
Момент инерции тела.
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают M. и. осевые и центробежные. Осевым M. и. тела относительно оси z наз. величина, определяемая равенством
где mi — массы точек тела, hi — их расстояния от оси z, r — массовая плотность, V — объём тела. Величина Iz является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой M. и. можно также выразить через линейную величину rz, наз. радиусом инерции относительно оси z, по ф-ле Iz = Mr 2 z, где M — масса тела. Размерность M. и.- L 2 M;единицы измерения -кг . м 2 .
Центробежными M. и. относительно системы прямоуг. осей х, у, z, проведённых в точке О, наз. величины, определяемые равенствами
или соответствующими объёмными интегралами. Эти величины являются характеристиками динамич. неуравновешенности тела. Напр., при вращении тела вокруг оси z от значений Ixz и Iyz зависят силы давления на подшипники, в к-рых закреплена ось.
M. и. относительно параллельных осей z и z’ связаны соотношением (теорема Гюйгенса)
где z’ — ось, проходящая через центр массы тела, d — расстояние между осями.
M. и. относительно любой проходящей через начало координат О оси Ol с направляющими косинусами a, b, g находится по ф-ле
Зная шесть величин Ix, Iy, Iz, Ixy, Iyz, Izx, можно последовательно, используя ф-лы (4) и (3), вычислить всю совокупность M. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно перпендикулярные оси, наз. гл. осями инерции, для к-рых Ixy = Iyz= Izx = 0. Тогда M. и. тела относительно любой оси можно определить, зная гл. оси инерции и M. и. относительно этих осей.
Источник