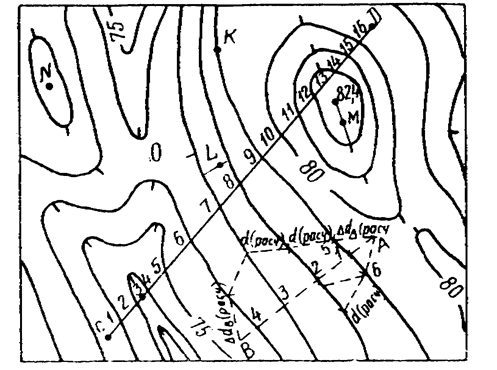
Аналитическое интерполирование
Из подобия соответствующих треугольников получаем:






Пример 1. Пусть отметки точек A и В будут: HA = 12,3 м; HB = 15,6 м. Расстояние между точками на плане l = 56,0 м. Принятая высота сечения рельефа hc = 1 м (рис. 27).
Решение. Между точками А и В пройдут горизонтали с отметками 13; 14; 15 м. Местоположение крайних горизонталей определится отрезками


Отложив в масштабе плана от точки А отрезок 11,9 м и от точки В отрезок 10,1 м, получим местоположение горизонталей 13,0 и 15,0. Разделив расстояние между этими крайними горизонталями пополам, находим местоположение горизонтали 14,0.
Пример 2. Пусть при тех же исходных данных hc = 0,5 м. Тогда между точками А и В пройдут горизонтали 12,5; 13,0; 13,5; 14,0; 14,5; 15,0; 15,5. Соответственно


Разделив расстояние между крайними горизонталями на шесть частей, определим местоположение оставшихся пяти горизонталей.
Графическое интерполирование
Такое интерполирование, по сравнению с аналитическим, позволяет выполнить работу быстрее, с обеспечением необходимой точности. При графическом интерполировании используют интерполятор. Для построения интерполятора на кальке тушью вычерчивают ряд параллельных прямых линий на одинаковом расстоянии одна от другой (через 2, 4, 5 или 10 мм в зависимости от крутизны скатов данной местности и высоты сечения рельефа).
Для определения местоположения горизонталей интерполятор накладывается так, чтобы число линий интерполятора между точками А и В (см. рис. 27) равнялось числу горизонталей на этом отрезке. Так, при исходных данных рассмотренного выше примера 1 отрезок АВ должны пересекать три линии интерполятора. Затем, поворачивая и смещая интерполятор, необходимо получить такое его положение, чтобы DdA составляло часть заложения d в соответствии с превышением DhA, и одновременно DdB также соответствовало превышению DhB. Оценка приведенных соответствий производится измерениями, при достаточном опыте – на глаз. Фиксировать на плане найденные точки местоположения горизонталей можно наколами иглы (обычно оказывается достаточным надавливание карандашом).
Интерполирование на глаз
При наличии достаточного опыта определение местоположения горизонталей производят на глаз, руководствуясь теми же положениями, которые приведены в аналитическом методе интерполяции. Практика показывает, что глазомерное интерполирование обычно обеспечивает точность в ¼hc, что соответствует точности съемки рельефа.
Построение горизонталей заключается в соединении плавными кривыми точек, найденных в результате интерполяции (аналитической, графической или на глаз). Начинать целесообразно с характерных по рельефу форм местности. Водораздельные и водосливные линии пересекаются горизонталями под прямыми углами.
Практическая часть
1. В пределах квадрата километровой сетки по двум сторонам квадрата определите направление повышения и понижения местности, руководствуясь берг-штрихами, надписями горизонталей, отметками характерных точек на карте.
2. Нанесите характерные линии рельефа. Характерными линиями рельефа являются водораздельные и водосливные линии. В центральной части карты опознайте две смежные возвышенности, разделенные лощиной. В пределах квадрата километровой сетки построить водосливную линию и на участках возвышенностей, непосредственно примыкающих к лощине, постройте водораздельные линии. При построении водосливных и водораздельных линий имейте в виду, что они пересекают горизонтали в местах их наибольшей кривизны. Водораздельные линии проходят также через точки с наибольшими отметками и через средние точки седловины.
3. Определите отметки всех горизонталей в пределах заданного квадрата километровой сетки.
8. РЕШЕНИЕ ЗАДАЧ ПО ТОПОГРАФИЧЕСКИМ КАРТАМ
Определение отметок точек
При решении задач данного типа возможны следующие пять случаев.
1. Точка К (рис. 28) лежит на горизонтали. Ее отметка определится отметкой горизонтали (Hk = 79,0 м).
2. Точка L находится между горизонталями с разными отметками. Проведя через точку L линию кратчайшего расстояния между горизонталями и применив линейную интерполяцию, определяем: HL = 77,6 м.
3. Точка М находится внутри замкнутой горизонтали и известна отметка характерной точки (вершины возвышенности) – 82,4. Проведя через точку с известной отметкой и точку М линию до горизонтали и применив линейную интерполяцию, находим: НМ = 82,2 м.
4. Точка N находится в центре замкнутой горизонтали, отметки характерной точки нет. В подобных случаях следуют правилу: превышение точки в центре замкнутой горизонтали принимается равным половине высоты сечения рельефа. Следовательно, в нашем случае
HN = 78,0 + 
5. Точка О находится в точке седловины. Здесь также принимается превышение 0,5hc, тогда НO = 76,5 м.
Отметки точек по топографическому плану или карте вычисляют с точностью 0,1hc.
Определение крутизны ската
Крутизна ската оценивается посредством измерения угла наклона линии к горизонту n или величины уклона i, та и другая характеристика может быть или положительной, или отрицательной. Обе величины можно вычислить, применив формулу i = tgn = 
Масштабы заложений строятся для определенной величины hc. Задаваясь различными значениями заложения горизонталей d (т.е. горизонтальное проложение между смежными горизонталями), можно вычислить угол n пo формуле tgn = 

Для того чтобы по имеющимся масштабам заложений определить крутизну ската, следует в раствор циркуля взять заложение d,приложить к масштабу заложения так, чтобы одна ножка циркуля была на основании шкалы, а другая – на кривой, при этом обе ножки должны быть на перпендикуляре к основанию шкалы.
Уклон является безразмерной величиной, его можно также записать в процентах (%) или в промиллях ( o /oo): i = 0,005 = 0,5 % = 5 o /oo .
Источник
Способы интерполирования горизонталей и особенности их проведения



Интерполяция (лат.) — вставка внутрь. Под интерполяцией в математике понимают всякий способ, с помощью которого можно по таблице найти промежуточные результаты, которых нет непосредственно в таблице.
При рисовке горизонталей на планах используют следующие способы интерполяции:
1.»На глаз» (визуально). Предположим, что на плане имеются три соседние точки с подписанными высотами 201.35, 203.30, 200.75. Необходимо провести горизонтали с высотой сечения рельефа 1.0 м, т.е. найти визуально плановое положение линий с высотами 201, 202 и 203 м.
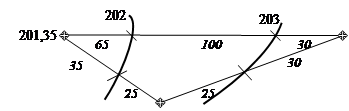 |
 |
|
|
Рис.18а. Интерполирование и проведение горизонталей «на глаз»
2. Аналитический, который предусматривает определять расстояние до горизонталей из прямо пропорциональной зависимости между превышением и горизонтальным проложением между точками с подписанными на плане высотами. Из рис.18б видно, что расстояния от точки А до горизонталей с высотами 202 и 203 d1 = h1 . dab/hab, d2 = h2 . dab/hab, где h1 и h2 — превышения между горизонталями с отметками 202 и 203 и точкой А с отметкой 201.35 (0.65 и 1.65 м); dab — расстояние, измеряемое на плане между пикетными точками;
| |
|



|
|

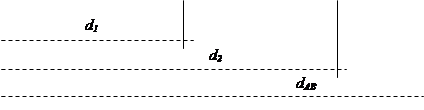 |
Рис.18б. Аналитический способ интерполяции горизонталей
3.Графический способ предусматривает использование палетки, представляющей собой прозрачный лист бумаги или пластика с нанесенным рядом параллельных линий (горизонталей) через 5. 10 мм друг одруга. Подписав на палетке отметки горизонталей, которые необходимо провести,и, поворачивая палетку на плане, совмещают точки с отметками с горизонталями на палетке, продавливают карандашом их на план(рис. 18в).
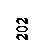   |
Рис.18в. Графический способ интерполяции горизонталей
Свойства горизонталей и особенности их проведения:
1. Горизонталь — линия равных высот т.е. все ее точки имеют одинаковую высоту;
2. Горизонталь должна быть непрерывной плавной линией;
3. Горизонтали не могут раздваиваться и пересекаться;
4. Расстояние между горизонталями (заложение) характеризуют крутизну ската. Чем меньше расстояние, тем круче скат;
5. Водораздельные и водосборные линии горизонтали пересекают под прямым углом;
6. В случаях, когда заложение превышает 25мм, проводят дополнительные горизонтали (полугоризонтали) в виде штриховой линии (длина штриха 5-6 мм, расстояние между штрихами 1-2 мм) 7. При окончательном оформлении плана выполняют некоторое сглаживание горизонталей в соответствии с общим характером рельефа, при этом предельная погрешность изображения рельефа горизонталями не должна превышать 1/3 основного сечения.
Источник
СПОСОБЫ ИНТЕРПОЛИРОВАНИЯ ГОРИЗОНТАЛЕЙ И ОСОБЕННОСТИ ИХПРОВЕДЕНИЯ.
Интерполяция (лат.) — вставка внутрь. Под интерполяцией в математике понимают всякий способ, с помощью которого можно по таблице найти промежуточные результаты, которых нет непосредственно в таблице
При рисовке горизонталей на планах используют следующие способы интерполяции:
1.»На глаз» (визуально). Предположим, что на плане имеются три соседние точки с подписанными высотами 201.35, 203.30, 200.75. Необходимо провести горизонтали с высотой сечения рельефа 1.0 м, т.е. найти визуально плановое положение линий с высотами 201, 202 и 203 м.
 |
 |
Рис.18а. Интерполирование и проведение горизонталей «на глаз» 2. Аналитический, который предусматривает определять расстояние до горизонталей из прямо пропорциональной зависимости между превышением и горизонтальным проложением между точками с подписанными на плане высотами. Из рис.18б видно, что расстояния от точки А до горизонталей с высотами 202 и 203 d1 = h1. dab/hab, d2 = h2. dab/hab, где h1 и h2 — превышения между горизонталями с отметками 202 и 203 и точкой А с отметкой 201.35 (0.65 и 1.65 м); dab — расстояние, измеряемое на плане между пикетными точками; hab — превышение между точками А и В (203.30 — 201.35 = 1.95 м). 3.Графический способ предусматривает использование палетки, представляющей собой прозрачный лист бумаги или пластика с нанесенным рядом параллельных линий (горизонталей) через 5. 10 мм друг одруга. Подписав на палетке отметки горизонталей, которые необходимо провести,и, поворачивая палетку на плане, совмещают точки с отметками с горизонталями на палетке, продавливают карандашом их на план(рис. 18в). Свойства горизонталей и особенности их проведения: 1. Горизонталь — линия равных высот т.е. все ее точки имеют одинаковую высоту; 2. Горизонталь должна быть непрерывной плавной линией; 3. Горизонтали не могут раздваиваться и пересекаться; 4. Расстояние между горизонталями (заложение) характеризуют крутизну ската. Чем меньше расстояние, тем круче скат; 5. Водораздельные и водосборные линии горизонтали пересекают под прямым углом; 6. В случаях, когда заложение превышает 25мм, проводят дополнительные горизонтали (полугоризонтали) в виде штриховой линии (длина штриха 5-6 мм, расстояние между штрихами 1-2 мм) 7. При окончательном оформлении плана выполняют некоторое сглаживание горизонталей в соответствии с общим характером рельефа, при этом предельная погрешность изображения рельефа горизонталями не должна превышать 1/3 основного сечения. ЗАДАЧИ, РЕШАЕМЫЕ НА ПЛАНАХ И КАРТАХ. СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ. Определение географических координат точек. Используя географические координаты углов трапеции, образованной пересечением меридианов и параллелей, а также внутреннюю (минутную) рамку карты находят географические широты (j) и долготы (l) точек. Например, для точек А и В, заданных на учебной карте масштаба 1:10 000 соответственно на пересечении улицы совхоза Беличи и дороги на восток и на ближайшем пересечении дорог, имеем jА = 54° 49’42» CШ, lА = 18° 04’56» ВД, jВ = 54° 40’40» СШ, lВ = 18° 06’50» ВД. Определение зональных прямоугольных координат точек. Для этого опускают перпендикуляры из заданной точки на линии координатной (километровой) сетки и измеряют их длины. Затем, используя масштаб карты и оцифровку координатной сетки, получают координаты, которые можно сравнить с географическими. Для точек А и В, имеем XА = 6 065.45 км, YА = 4 311.85 км ( -188.15 км), XВ = 6 065.20 км, YВ = 4 313.82 км ( -186.18 км). Откуда следует, что точки А и В расположены западнее осевого меридиана четвертой шестиградусной зоны на 188.15 и 186.18 км соответственно. Определение дирекционного угла, истинного и магнитного азимутов заданного направления. Для определения дирекционного угла линии АВ с помощью транспортира измеряют на карте по ходу часовой стрелки горизонтальный угол между северным направлением осевого меридиана зоны (линией координатной сетки) и заданным направлением. В нашем примере дирекционный угол направления АВ aАВ = 94° 45′. Истинный азимут отличается от дирекционного угла на величину сближения меридианов (+g), а магнитный азимут отличается от истинного на величину склонения магнитной стрелки (+d). Из схемы взаимного расположения осевого, истинного и магнитного меридианов, находящейся под южной рамкой карты, видно, что на этом листе карты истинный азимут Аи меньше дирекционного угла a на величину сближения меридианов g = 2° 22′, а магнитный азимут Ам меньше истинного на величину склонения магнитной стрелки d = 6° 12′. Следовательно, АиАВ = aАВ — g = 94° 45′ — 2° 22′ = 92° 23′, АмАВ = АиАВ- d = 92° 23′ — 6° 12′ = 86° 11′. Определение высоты точек и уклона линии. Высоты точек на карте определяют графически, интерполированием между соседними горизонталями. В нашем примере высоты точек НА = 155.2 м, НВ = 143.2 м. Тогда уклон линии АВ iАВ = (НВ — НА) / dАВ = -12.0 / 2000 = -0.006 = -60/00 , где dАВ — горизонтальное проложение линии АВ, равное 2000 м. На строительных чертежах направление уклона обычно показывают стрелкой, над которой записывают его величину в промиллях (тысячных долях), а под стрелкой — горизонтальное проложение. Построение профиля местности по линии АВ. На миллиметровой бумаге строят графы профиля, в которые записывают номера характерных точек рельефа местности по линии АВ, расстояния между ними и их высоты. Горизонтальный масштаб профиля принимают равным масштабу карты. Вертикальный масштаб, по которому откладывают высоты от выбранного условного горизонта, обычно принимают в 10 раз крупнее горизонтального, т. е. 1:1000. Полученные точки на профиле соединяют ломаной линией. Проведение на карте между точками А и В кратчайшей линии с заданным уклоном. Вычисляют величину заложения (расстояния между горизонталями) d по формуле d = h /i, где h — высота сечения рельефа горизонталями. В нашем примере d = 2.5 / 0.006 = 402 м. Это заложение в масштабе карты берут в раствор измерителя и из точки А этим расстоянием засекают на соседней горизонтали точку, от которой тем же раствором засекают следующую точку на соседней горизонтали и т. д. Соединив последовательно все точки, получают ломаную линию с уклоном, равным заданному. На планах масштаба 1:1000 удобно при построении линии заданного уклона пользоваться графиком заложений по уклонам, который строят по табличным данным, вычисленным по формуле d = hc/i. При построении графика на горизонтальной прямой откладывают произвольной величины равные отрезки и надписывают величины уклонов. Из полученных точек вверх по вертикали откладывают соответствующие уклонам величины заложений в масштабе плана. Соединив точки плавной линией, получают график заложений по уклонам. Определение площади аналитическим, графическим (геометрическим) и механическим способами. При аналитическом способе площадь любого многоугольника, заданного координатами вершин вычисляется по следующим формулам: Р = 1/2 SХi (Уi+1 — Уi-1), Р = 1/2 SУi (Хi-1 — Хi+1), где i — порядковый номер вершин многоугольника, изменяющийся от 1 до N (числа вершин). Относительная погрешность вычисления площади зависит в основном от погрешностей координат точек и составляет около 1/2000. Графический способ определения площади предусматривает разбивку контура на элементарные геометрические фигуры (треугольники, четырехугольники и трапеции), площади которых вычисляют по измеренным на карте с учетом масштаба длинам сторон и высот. Относительная погрешность суммарной площади, полученной графически, обычно составляет более 0.5-1.0% (1/100). Механический способ основан на применении специального прибора -полярного планиметра, который состоит из полюсного и обводного рычагов и счетного механизма. Перед измерением площади контура вычисляют цену деления планиметра с — площадь, соответствующую одному делению планиметра. Для этого на карте обводят планиметром один квадрат километровой сетки с известной площадью Ризв.= 100 га. Отсчеты по счетному механизму берут до обводки n1 и после обводки n2, вычисляют их разность DU, которую уточняют несколько раз. Например, n1 = 3546, n2 = 4547. Тогда цена деления планиметра с = Ризв./DU = 100/1001=0.09990 га. Площадь заданного контура сначала получают в результате обводки в делениях планиметра МU, а затем, используя цену деления с, — в гектарах Р = с . DU. Контроль полученных результатов выполнятся повторными измерениями и вычислениями цены деления планиметра и определяемой площади. Относительная погрешность измерений площади планиметром составляет порядка 1/300 Дата добавления: 2019-02-26 ; просмотров: 2786 ; Мы поможем в написании вашей работы! Источник |