Аналитическим способом вычислить количество маршрутов длины

Теория.

Дата добавления: 2015-07-23 ; просмотров: 1088 ; Нарушение авторских прав

Подграф исходного графа — граф, содержащий некое подмножество вершин данного графа и все рёбра, инцидентные данному подмножеству.

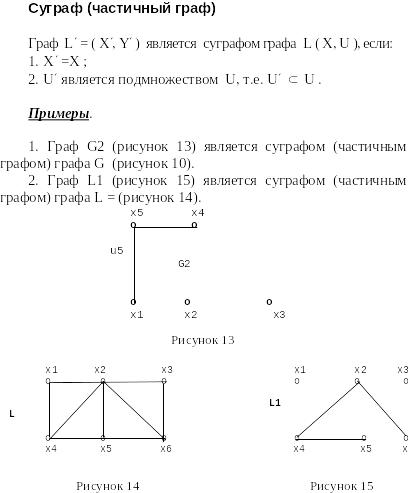
Частичный граф (суграф) исходного графа — граф, содержащий все вершины исходного графа и подмножество его рёбер.

1) Граф G1 (рис. 1.1) является подграфом графа G (рис. 1).

2) Граф G2 (рис. 1.2) является суграфом графа G (рис. 1).

Выполнить бинарные операции над графами ( , ∩,).

1) Граф G1 (рис. 1.1) является подграфом графа G (рис. 1).

Матрица смежности графа G1:

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

2) Граф G2 (рис. 1.2) является суграфом графа G (рис. 1).

Матрица смежности графа G2:

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

Объединение G3 = G1 G2 :

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

Пересечение G4 = G1∩ G2:

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

Определить аналитическим способом число маршрутов длины L = 3 для каждой пары вершин графа своего варианта.

Теория.Для определения маршрутов длины L=3 в графе его матрицу смежности возводят в степень, равную L. Тогда для каждого значения степени L значение элемента матрицы определяет количество маршрутов длиной L. В нашем случае возводим матрицу R в куб.

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

Каждый r_i,j-й элемент матрицы R 3 равен числу маршрутов длиной 3, ведущих из вершины x_i в x_j.

Построить все маршруты длины L = 3 между вершинами, указанным преподавателем.

Рассмотрим вершины х3 и х5. r_3,5= 6 означает, что в графе 6 маршрутов длины L=3 , ведущих из x₃ в x₅ :

Построить метрику графа своего варианта (рис.1). Определить радиус, диаметр графа, периферийные и центральные вершины.

1. Задаём матрицу метрики M=(m_i,j)_nxn. Размерность матрицы M равна размерности матрицы R. Все элементы mi,j матрицы M не определены.

2. Начальное значение степени k матрицы S равно 1: k=1. Главной диагонали матрицы M присваиваем значения 0.

3. Всем элементам m_i,j, значения которых не определены, присвоить значение степени k, если соответствующие им элементы матрицы S k ≠ 0.

4. Проверяем, в матрице M имеются элементы m_i,j, значения которых еще не определены? Если такие элементы имеются, то переходим к шагу 4; в противном случае – к шагу 7.

5. Повышаем степень k матрицы R: k=k+1.

6. Проверяем, является ли матрица R k -1 устойчивой. Если матрица R k -1 – неустойчивая, то переходим к пункту 3. Иначе – переходим к пункту 7.

7. Всем элементам m_i,j матрицы M, значения которых остались неопределёнными, присваиваем значение бесконечность.

Булевская матрица смежности R=

x1	x2	x3	x4	x5	x6	x7
x1

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

Единичная матрица E=

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

Полученная суммарная матрица S=R+E:

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

Возведём матрицу S с обнулённой главной диагональю в степень 1 и заменим все элементы неравные 0 на 1.Все остальные элементы остаются неопределёнными. Это и есть фундамент матрицы метрики.

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

При последовательном возведении матрицы в степень получаем соответствующую матрицу метрики:

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

х1	х2	х3	х4	х5	х6	х7
х1
х2
х3
х4
х5
х6
х7

В полученной матрице метрики не осталось неопределенных мест, значит, она построена.

Определим радиус, диаметр, центральные и периферийные вершины.

Матрица метрики и максимальные значения элементов

max

х1

х2

х3

х4

х5

х6

х7

Наибольшее из значений – диаметр графа D=3.

Наименьшее из значений – радиус графа R=2.

Вершины, имеющие наибольшую удаленность равную диаметру, называются периферийными.

Периферийные вершины: х2, х5, х7.

Вершины, имеющие наибольшую удаленность равную радиусу, называются центральными.

Центральные вершины: х1, х3, х3, х6.

Не нашли то, что искали? Google вам в помощь!

Источник

Клуб студентов «Технарь». Уникальный сайт с дипломами и курсовыми для технарей.

Все разделы / Дискретная математика /

Лабораторная работа №1 по дисциплине: Дискретная математика. Вариант №24

Тип работы: Работа Лабораторная
Форматы файлов: Microsoft Word
Сдано в учебном заведении: ТУСУР

Описание:
Цель лабораторной работы
Изучить основные понятия, определения и терминологию теории графов, классы графов, способы задания графа, простейшие операции на графах, числовые характеристики графа и способы их вычисления.

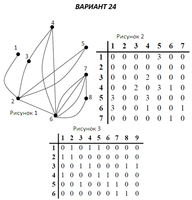
Задание 1. По матрицам (рис. 2 и 3) построить диаграммы графов, определив предварительно вид данных матриц.

Задание 2. Методами поиска «в глубину» и «в ширину» найти наибольший минимальный маршрут между вершинами графа (рис. 1).

Задание 3. Для каждой пары вершин графа (рис. 1) аналитическим способом вычислить количество маршрутов длины, равной 4, и выделить те пары вершин, для которых их количество ≥ 3, но не более 10. Выписать эти маршруты для какой-либо из выделенных пар. В описании маршрутов указывать вершины и ребра, входящие в него.

Задание 4. Построить матрицу метрики графа (рис. 1).
Для этого для матрицы связности R найдём S^1=R+E, затем каждый шаг будем получать 〖S^i〗^\’=S^(i-1) S, для всех ячеек, которые являются нулевыми в S^(i-1) и ненулевыми в S^i\’ зададим значение i, прочие скопируем из S^(i-1) в S^i. Если S^(i-1)=S^i, то завершаем алгоритм, находя матрицу метрики M, копируя туда все ненулевые ячейки из S^i, а вместо нулевых задавая ∞, m_ii=0.

Задание 5. С помощью алгоритма Магу – Вейсмана выполнить правильную раскраску вершин графа с минимальным количеством цветов.

Задание 6. Определить число вершинного покрытия графа (рис. 1).
На основании
x_1 x_4 x_5 x_8+x_1 x_4 x_5 x_7+x_1 x_3 x_5 x_8+x_1 x_3 x_5 x_7+x_1 x_3 x_5 x_6+x_1 x_5 x_6+x_2 x_4 x_8+x_2 x_4 x_7+x_2 x_8+x_2 x_7+x_6
из предыдущего задания, имеем число вершинного покрытия равным 4.

Задание 7. Определить, содержит ли граф (рис. 1) эйлерову цепь или эйлеров цикл.
Ответ обосновать.

Задание 8. Аналитическим способом определить число компонент связности графа. 9

Комментарии: Помогу с вашим вариантом, другой работой или дисциплиной.
E-mail: sneroy20@gmail.com

Размер файла: 211,8 Кбайт
Фаил: (.docx)
——————-
Обратите внимание , что преподаватели часто переставляют варианты и меняют исходные данные!
Если вы хотите, чтобы работа точно соответствовала, смотрите исходные данные. Если их нет, обратитесь к продавцу или к нам в тех. поддержку.
Имейте ввиду, что согласно гарантии возврата средств, мы не возвращаем деньги если вариант окажется не тот.
——————-

Источник

Справка по идз «Графы»

Скелет графа общего вида. В случае, когда при исследовании графа L=(X.U;P) общего вида требуется не полная информация о нём, а лишь знание того, какие пары его различных вершин смежны и какие нет, прибегают к носителю такой информации – скелету графа L, который обозначим как . Граф относится к классу обыкновенных графов с множеством вершин тем же, что и в графе L, и новым множеством рёбер , определённым следующим образом:

если в графе L есть петли, то они удаляются;

если в графе L есть дуги, то производится дезориентация дуг;

если в графе L есть кратные рёбра, то они заменяются одним эквивалентным ребром-звеном;

оставшиеся рёбра образуют множество рёбер .

Таким образом, множество рёбер состоит из рёбер, полученных из множества U после выполнения описанных выше процедур 1, 2, 3.

1.3. Определение числа маршрутов длины «l» на графе

Маршрутом _i,j в графе G=(X,U) называется конечная последовательность вершин и рёбер вида –

где x₀, x_l – соответственно начальная и конечная вершины маршрута _0,l .

Очевидно, в конечном графе G=(X,U) можно выделить только конечное число маршрутов. Длина маршрута _i,j равна числу рёбер, которые в него входят.

Часто требуется знать, сколько маршрутов заданной длины в графе G связывает вершину x_i с вершиной x_j .

Для определения маршрутов длины q в графе G=(X,U) его матрицу смежности R возводят в степень, равную q. Тогда для каждого значения степени q=1,2,…,k значение элемента (r_i,j) q матрицы R q определяет количество маршрутов _i,j длиной, равной значению степени q.

Рисунок 3

ПРИМЕР. Для графа G= (X,U) , представленного на рисунке 3, определить количество маршрутов длины, равной 2.

Матрица смежности R графа G имеет вид:

Возведем матрицу R в квадрат:

Значение каждого элемента r_i,j матрицы R 2 равно числу маршрутов длины 2, ведущих из вершины x_i в вершину x_j.

Например, r_3,2=2 означает, что в графе два маршрута длины 2, которые ведут из вершины x₃ в вершину x₂ . Запишем их:

Для графа, представленного на рисунке 1 выполнить следующее:

4.1. Привести примеры подграфов 3-х вершинных, 4-х вершинных, 1-вершинных.

4.2. Привести пример суграфа данного графа.

4.3. Выполнить унарные операции для вершин, помеченных *.

Для графа G=(X,U) ( рисунок 1) выполнить следующее:

5.1. Построить матрицу метрики (отклонений).

5.2. Вычислить радиус и диаметр.

5.3. Определить периферийные точки.

Способ нахождения метрики графа

Для нахождения метрики = графа L = (X,U) достаточно знать его матрицу смежности R=< r_i,j> над булевой алгеброй B = ( 0,1 ), т.е. элементы матрицы r_i,j = 1, если вершины x_i и x_j – смежны и r_i,j = 0, в противном случае, все действия над элементами матрицы R производятся по правилам логической алгебры:

1 + 1 = 1; 0 + 0 = 0; 1 + 0 = 1; 0 * 0 = 0; 1 * 0 = 0.

Сопоставляя уже известные нам способы для установления существования маршрутов в графе длины q = m, можно утверждать, что при возведении в степень матрицы S = R + E, где Е – единичная матрица той же размерности, что и размерность матрицы R, на некотором шаге возведения в степень получим:

S = S k+1 , т.е. устойчивую матрицу S в степени «k».

Значения степеней p матрицы S p : p= равны длинам простых кратчайших цепей, связывающих вершины x_i и x_j.

Таким образом, последовательно возводя в степень p = <1, 2, 3,…, k>матрицу S до получения устойчивой матрицы S k , можно определить расстояния между всеми вершинами графа L=(X,U), построив матрицу метрики графа L.

Алгоритм построения матрицы метрики графа

Исходные данные для построения матрицы метрики (отклонений):

2. Матрица смежности R графа L c элементами логического типа:

 1, если вершины x_i, x_j – смежны;

Источник