Анаграмма торт сколькими способами

Содержание

Переставляем буквы. Уровень 1. Дима и Вова играли в анаграммы. Вова написал 4 буквы, а Дима должен был догадаться, какое слово Вова имел в виду. Сколькими способами Вова мог загадать слово ТОРТ?
13. Перестановки с повторениями
Комбинаторика 5
Анаграмма торт сколькими способами

Переставляем буквы. Уровень 1.
Дима и Вова играли в анаграммы.
Вова написал 4 буквы, а Дима должен был догадаться, какое слово Вова имел в виду.
Сколькими способами Вова мог загадать слово ТОРТ?

Решим задачу по комбинаторике:
Анаграмма из слова ТОРТ (само слово «ТОРТ» Вова написать не мог): 4 буквы, из них Т повторяется два раза:
4!/2=1*2*3*4/2=24:2=12 способов
Т.к. слово ТОРТ Вова написать не мог, значит 12-1=11 способов
Ответ: Вова мог загадать слово ТОРТ 11 способами.

Проверим:
трот
трто
ттор
ттро
тотр
оттр
отрт
ортт
ротт
ртот
ртто
+ торт (не считаем, т.к. из этого слова нужно составить анаграмму).

1) sin105= sin(60+45)= sin60*cos45+cos60*sin45= √3/2 * √2/2 + 1/2 * √2/2= √6/4 + √2/4= (√6+√2)/4

2) sin(180-a)+cos(90+a)= sina+(- sina)= sina -sina =0

3) cos 40/sin40 * sin140/cos140 = (cos40*sin140)/(sin40*cos140)= 1/2 [sin(40+140)-sin(40-140)]/ 1/2 [sin(40+140)+sin(40-140)] = (sin180+sin100)/(sin180-sin100) = sin100/ (-sin100)= -1

При решении таких уравнений используются несколько приёмов:

I. При переносе величин в противоположную сторону равенства знак меняется на противоположный!

II. Знак перед скобками распространяется на все слагаемые!

III. Двойной знак минус «–» перед числом даёт плюс «+», что логично, поскольку знак минус «–» даёт противоположное число, и если, например, для +7 противоположным является число –7, то для числа –7 противоположным будет как раз +7, поэтому и выходит, что –(–7) = +7.

IV. Любое уравнение можно «перевернуть» слева направо, т.е. всю левую часть записать справа, а всю правую – слева.

V. Обе части уравнения можно разделить на одно и то же число, умножить на одно и то же число или можно прибавить к обеим частям уравнения одно и то же число.

VI. Подобными называют слагаемые, представленные в виде числа, умноженного на переменную. Такие слагаемые можно складывать и вычитать, если они содержат одну и ту же переменную.

Источник

13. Перестановки с повторениями

При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет . Мы имеем здесь дело с перестановками с повторениями.

Общую задачу сформулируем следующим образом.

Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, . Сколько можно составить различных перестановок из этих элементов?

Число перестановок c повторениями обозначают . Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом способами так, что она остаётся неизменной.

Число различных перестановок с повторениями, которые можно составить из данных элементов, равно

, (11.1) где .

Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:

Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?

Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем

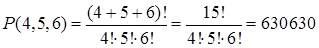
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?

Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:

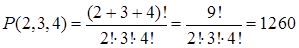
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?

Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем

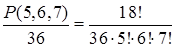
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?

Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим

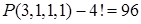
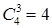
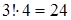
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить способами. Всего получаем способа.

11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?

Ответ: .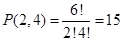

11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?

Ответ: .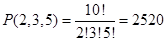

11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?

Ответ: .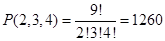

11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?

Ответ: .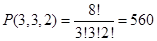

11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?

Ответ: .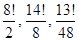

11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?

Ответ: .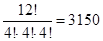

11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?

Ответ: .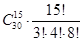

11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?

Ответ: .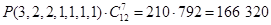

11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?

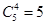
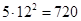
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать способами. Всего способов.

Источник

Комбинаторика 5

Во многих комбинаторных задачах непосредственное нахождение числа интересующих нас вариантов оказывается затруднительным. Однако при некотором изменении условия задачи можно найти количество вариантов, превосходящее исходное в известное число раз. Такой прием называется методом кратного подсчета.

1. Сколько анаграмм имеет слово КЛАСС?

Трудность в том, что в этом слове две одинаковые буквы С. Будем временно считать их разными и обозначим С₁ и С₂. Тогда число анаграмм окажется равным 5! = 120. Но те слова, которые отличаются друг из друга лишь перестановкой букв С₁ и С₂, на самом-то деле являются одной и той же анаграммой! Поэтому 120 анаграмм разбиваются на пары одинаковых, т.е. искомое число анаграмм равно 120/2 = 60.

2. Сколько анаграмм имеет слово ШАРАДА?

Считая три буквы А различными буквами А₁, А₂, А₃, получим 6! анаграмм. Но слова, которые получаются друг из друга только перестановкой букв А₁, А₂, А₃, на самом деле являются одной и той же анаграммой. Поскольку имеется 3! перестановок букв А₁, А₂, А₃, полученные изначально 6! анаграмм разбиваются на группы по 3! одинаковых, и число различных анаграмм оказывается равным 6!/3! = 120.

Другая содержательная комбинаторная идея — так называемый переход к дополнению. В некоторых задачах вместо искомого числа «нужных» вариантов оказывается проще найти число «ненужных» вариантов, дополняющее число «нужных» вариантов до известного общего количества.

3. Сколько существует четырехзначных чисел, в записи которых есть хотя бы одна четная цифра?

Найдем количество «ненужных» четырехзначных чисел, в записи которых присутствуют только нечетные цифры. Таких чисел 5 4 = 625. Но всего четырехзначных чисел 9000, поэтому искомое количество «нужных» чисел равно 9000 – 625 = 8375.

Найти число анаграмм у слов ВЕРЕСК, БАЛАГАН, ГОРОДОВОЙ.
Найти число анаграмм у слов БАОБАБ, БАЛЛАДА, ПЕРЕПОЛОХ, АНАГРАММА, МАТЕМАТИКА, КОМБИНАТОРИКА, ОБОРОНОСПОСОБНОСТЬ.
Сколькими способами можно поселить 7 приезжих в три гостиничных номера: одноместный, двухместный и четырехместный?
В холодильнике лежат два яблока, три груши и четыре апельсина. Каждый день в течение девяти дней подряд Пете дают один какой-то фрукт. Сколькими способами это может быть сделано?
Из семи лучших лыжников школы нужно отобрать команду из трех человек для участия в городских соревнованиях. Сколькими способами это можно сделать?
Перед экзаменом профессор пообещал поставить двойки половине экзаменуемых. На экзамен пришло 20 студентов. Сколькими способами он может выполнить обещание?
Сколько слов можно составить из пяти букв А и не более чем из трех букв Б?
В продаже есть шоколадное, клубничное и молочное мороженое. Сколькими способами можно купить три мороженых?
При приготовлении пиццы к сыру добавляются разные компоненты, обеспечивающие тот или иной вкус. В распоряжении Билла имеются лук, грибы, помидоры, перец и анчоусы, причем все это, по его мнению, можно добавлять к сыру. Сколько видов пиццы может приготовить Билл?
Свидетель криминальной разборки запомнил, что преступники скрылись на «мерседесе», номер которого содержал буквы Т, З, У и цифры 3 и 7 (номером является строка, в которой сначала идут три буквы, а затем — три цифры). Сколько существует таких номеров?
Сколько диагоналей в выпуклом n-угольнике?
Сколько всего существует n-значных чисел?
Сколько существует десятизначных чисел, в записи которых есть хотя бы две одинаковые цифры?
Кубик бросают трижды. Среди всевозможных последовательностей результатов есть такие, в которых хотя бы один раз выпала шестерка. Сколько их?
Сколько пятизначных чисел имеют в своей записи цифру 1?
Сколькими способами можно расставить на шахматной доске белого и черного короля так, чтобы они не били друг друга?
Сколько делителей у числа 10800?