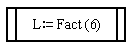Алгоритмы
Алгоритмы. Разработка алгоритма решения задачи
Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.
Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
,
где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем | ||||||||||||||
| |||||||||||||||
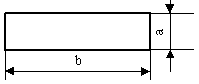
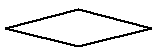
| Границы цикла | Верхняя граница | ||||||||||||||
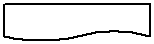
| Подготовка | Отображает модификацию команды или группы команд с целью воздействия на некоторую последующую функцию | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Рис. 1. Одномерный массив q
Массив имеет имя q . Для того чтобы можно было отличить одну ячейку массива от другой ячейки этого же массива, их нумеруют. Нумерация ячеек обычно начинается с 1. Номер ячейки массива называется его индексом , а константа в ячейке – элементом массива. Теперь становится возможной работа с отдельной ячейкой такого массива. Например, команда q7 = 8.2 означает, что в 7-ю ячейку массива q надлежит записать константу 8.2. Команда r41 = q2 + q5 означает, что нужно сложить константы, записанные во 2-ю и 5-ю ячейки массива q, и результат записать в 41-ю ячейку одномерного массива r . Эту же операцию можно описать другими словами: 41-му элементу массива r присвоить значение суммы 2-го и 5-го элементов массива q.
Двумерный массив по расположению ячеек напоминает математическую матрицу (рис. 2). Элемент такого массива характеризуется двумя индексами: первый показывает строку, в которой расположена ячейка, второй – ее столбец. Например, команда d 2, 5 = 43 означает, что в ячейку, размещенную на пересечении 2-й строки и 5-го столбца двумерного массива d , нужно записать константу 43.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 |
Рис.2. Двумерный массив d
Аналогично устроена структура массивов трех- и большей размерности.
5. Линейные алгоритмы
Линейный алгоритм – это алгоритм, в котором блоки выполняются последовательно сверху вниз от начала до конца.
На рис. 3 приведен пример блок-схемы алгоритма вычисления периметра Р и площади S квадрата со стороной длины A.
Блок-схема алгоритма состоит из шести блоков. Выполнение алгоритма начинается с блока 1 «Начало». Этот блок символизирует включение автомата, настройку его на выполнение алгоритма и выделение памяти под все переменные, которые задействованы в алгоритме. В алгоритме рис. 3 таких переменных три: A, Р, S . Следовательно, под каждую из них алгоритмом будет выделено по одной ячейке памяти. На этом блок 1 будет отработан.
Как видно из рис.3, блок 1 связан вертикальной линией потока с блоком 2. Эта линия не имеет стрелки, указывавшей направление потока. Следовательно, этот поток направлен вниз. Таким образом, после выполнения блока 1 управление будет передано на блок 2. Блок 2 «Перфокарта» ( см. табл. 1) показывает, что переменной A следует присвоить значение. Это означает, что в ячейку, отведенную автоматом под эту переменную, нужно поместить константу. На реальной компьютере эта константа может быть введена самыми разными способами. Способ зависит от того, как запрограммирован данный фрагмент. Можно, например, потребовать ввод константы с клавиатура или получить его из заранее подготовленного файла. Возможно эта константа будет получена через внешние источники данных, например, от физической установки, подключенной к компьютеру.
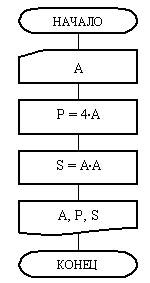
Рис. 3. Линейный алгоритм
Для данного примера способ передачи константы не имеет значения, важно лишь то, что при выполнении блока 2 в ячейку с адресом А будет занесена конкретная константа. Пусть такой константой является число 5.
Далее управление по линии потока передается к блоку 3 «Процесс». В этом блоке при выполнении размещенной в ней команды число 4 умножается на константу, помещенную в ячейку А (т. е. 5), и результат (т. е. 20) присваивается переменной Р (т. е. константа 20 записывается в ячейку по адресу Р). После выполнения этих операций управление передается к блоку 4.
В блоке 4 аналогичным образом производится умножение значений переменной А и результат (константа 25) присваивается переменной S (в ячейку по адресу S будет занесена константа 25). После этого выполняется переход к блоку 5.
При выполнении команд блока 5 выводятся (например, на экран, бумагу, во внешний файл и т. д.) значения переменных А, Р, S, которые сохранились в соответствующих ячейках к этому моменту. Понятно, что для конкретного примера А = 5 будут выведена константы 5, 20, 25, т. е. длина сторона квадрата, его периметр и площадь. Далее управление передается последнему блоку 6.
В блоке б “ Конец ” производится освобождение ячеек памяти, которые были зарезервированы под переменные А, P, S , и алгоритм заканчивает работу.
Понятно, что при новом запуске этого же алгоритма можно получить совсем другие числа. Так, если в блоке 2 переменной А присвоить значение 20, то алгоритм выдаст в блоке 5 константы 20, 80, 400.
Детальное описание алгоритма рис. 3 приведено для того, чтобы показать, в какой последовательности автомат выполняет предписанные операции и как при этом меняется состояние памяти автомата, т. е. для того, чтобы объяснить суть происходящих в автомате процессов. Из сказанного нужно уяснить, что автомат выполняет предписанную ему работу шаг за шагом. Всякий шаг обрабатывается процессором. Помимо вычислений процессор при необходимости отдает команды считывавшей/записывавшей головке, что и куда записывать, откуда читать. Конечный результат следует искать в ячейках памяти, каждая из которых до окончания алгоритма имеет известный адрес и хранит записанную в нее константу.
При выполнении контрольной или курсовой работы нет нужды давать столь подробное описание алгоритма. Тем не менее, описание должно быть выполнено с той степенью полноты, которая позволяет дать ясное представление о всех сторонах и особенностях алгоритмического процесса.
6. Разветвляющиеся алгоритмы
На практике алгоритмы линейной структуры встречается крайне редко. Чаще необходимо организовать процесс, который в зависимости от каких-либо условий проходит по той либо иной ветви алгоритма. Такой алгоритм называется разветвляющимся.
В блок-схемах ветвление начинается на выходах символа «Решение», с помощью которого в алгоритме выполняется проверка какого-либо условия. Количество ветвей тем больше, чем больше проверяемых условий.
Для пояснения рассмотрим решение задачи нахождения значения функции z = y/x.
На первый взгляд представляется, что алгоритм решения этой задачи имеет линейную структуру. Однако, если учесть, что делить на нуль нельзя из-за переполнения ячейки, то, во-первых, нужно из вычислений исключить вариант х = 0 и, во-вторых, проинформировать пользователя алгоритма о возникшей ошибке. Если этого не сделать, то при вычислениях может возникнуть аварийный выход до получения результата. В профессиональной практике аварийные завершения крайне нежелательны. т. к. к этому моменту уже может быть накоплено определенное количество результатов, которые окажутся необработанными и попросту пропадут. Можно привести другие примеры, когда аварийный останов компьютера может повлечь куда более серьезные последствия.
Решение задачи представлено блок-схемой рис. 4.
Она состоит из 7 блоков. После начала работы алгоритм в блоке 2 требует ввода аргументов X и Y. Затем в блоке 3 производится проверка условия X = 0. Здесь автомат проверяет равна ли нули константа, введенная в ячейку с адресом X. Результатом такой проверки является ответ «Да» или «Нет». В зависимости от этого ответа выполнение алгоритма пойдет по одной или другой ветви. Если результат проверки окажется отрицательным, то на х можно делить и управление передается блоку 4.
В блоке 4 будет получен результат Z, затем в блоке б значения всех трех переменных будут отпечатаны и в блоке 7 алгоритм закончит работу. Если же ответ окажется положительным, то управление будет передано блоку 4. Выполняя команду блока 4, автомат выведет сообщение «Ошибка» и затем закончит работу в том же блоке 7.
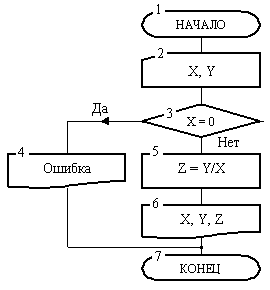
Рис. 4 . Разветвляющийся алгоритм
7. Циклические алгоритмы
Часто при решении задач приходится повторять выполнение операций по одним и тем же зависимостям при различных значениях входящих в них переменных и производить многократный проход по одним и тем же участкам алгоритма. Такие участки называются циклами. Алгоритмы, содержащие циклы, называется циклическими. Использование циклов существенно сокращает объем алгоритма.
Различают циклы с наперед известным и наперед неизвестным количеством проходов.
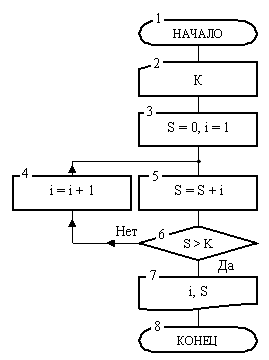
Пример 1. Рассмотрим пример алгоритма с циклом, имеющим наперед неизвестное количество проходов. Для этого решим следующую задачу. Указать наименьшее количество членов ряда натуральных чисел 1, 2, 3, . сумма которых больше числа К.
Блок-схема алгоритма решения этой задачи приведена на рис. 5. Она состоит из восьми блоков.
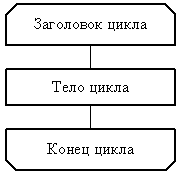
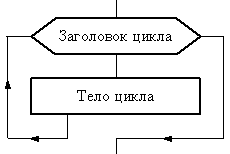
На рис. 6. показана структура цикла, которая может быть использована, когда условие выхода из цикла определяется символом его начала или символом его конца. Наряду с этим в качестве заголовка цикла может быть использован и символ «Подготовка». Структура такого цикла показана на рис. 7.
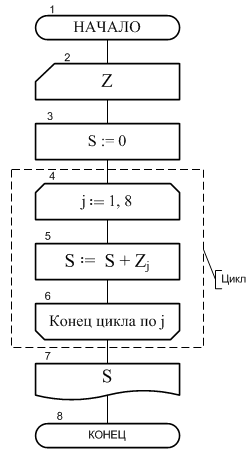
Пример 2. Теперь приведем пример алгоритма, содержащего цикл с наперед известным количеством проходов (повторений). Алгоритм решает задачу накопления суммы положительных элементов одномерного массива Z длины N (под длиной массива понимается количество его элементов).
Блок-схема алгоритма дана на рис. 8 . Вначале в блоке 2 производится ввод двух переменных N и Z. Первая из них представляет одну ячейку. В нее записывается константа – число, равное количеству элементов массива Z. Именно такое количество ячеек объединяет другая переменная – массив Z .
Следует подчеркнуть, что если бы ввод этих переменных в блоке 2 производился в противоположном порядке, то это привело бы к ошибке. Действительно, невозможно заполнить N ячеек массива Z, когда значение переменной N еще не известно.
Далее в блоке 3 переменной S присвоено начальное значение 0. Это сделано для того, чтобы приготовить ячейку к накоплению необходимой суммы.
Блоки 4-7 представляет собой цикл, в котором накапливается сумма. Заголовок цикла представлен блоком 4. Роль счетчика цикла играет переменная j , которая будет изменяться в цикле изменяться от 1 до N . Поскольку шаг изменения счетчика j явно не указан, то по умолчанию он подразумевается равным 1. Тело цикла образуют блоки 5 и 6.
Сразу после входа в цикл переменная j примет начальное значение j = 1. Далее в блоке 5 выполняется проверка положительности первого элемента массива Z (т. к . j = 1). Если этот элемент действительно положителен, то в блоке б значение элемента будет добавлено к переменной S , после чего в блоке 7 выполнится возврат к заголовку цикла. Если этот элемент неположителен (т. е. нуль или отрицательный), то оператор суммирования не будет исполнятся.
На втором круге цикла счетчик j в заголовке увеличится на 1 и станет равным 2. Теперь, при новом выполнении тела цикла, в блоке 5 проверяется на положительность второй элемент массива Z и , если он положителен , то добавляется в сумму и т. д. Последний раз тело цикла выполнится при i = N . При этом значении счетчика проверяется последний элемент массива. Наконец, в заголовке цикла i примет значение N +1. Это значение выходит за предписанный предел, следовательно, произойдет выход из цикла и управление перейдет блоку 8 . В этом блоке выводится накопленная сумма и алгоритм закончит работу в блоке 9.
Рис. 8. Циклический алгоритм
Тест на алгоритм Министерства образования и науки РФ
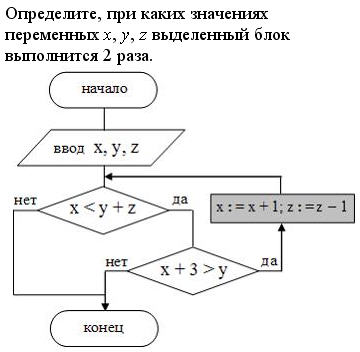
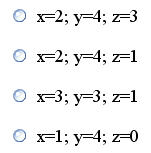
Условие : x
Условие : x + 3 > y
Выделенный блок
Таким образом, выделенный блок выполнится при x = 2; y = 4; z = 1 (вариант 2 ).
8. Алгоритмы со структурами вложенных циклов
Нередко при алгоритмическом решении задачи возникает необходимость создания цикла, содержащего в своем теле другой цикл. Такие вложенные друг в друга циклы относятся к структурам вложенных циклов. Порядок вложенности циклов, когда в теле внутреннего цикла содержатся другие циклы, может быть достаточно большим. Этот порядок определяется методом, с помощью которого достигается решение поставленной задачи. Так, при обработке одномерных массивов, как правило, удается построить алгоритмическую схему без вложения циклов. Однако в ряде случаев при решении таких задач без вложенных циклов не обойтись.
Отметим, что все вложенные друг в друга циклы, включая наружный, должны иметь счетчики с различными именами. Вне этих циклов счетчики могут быть использованы как обычные переменные или как счетчики других циклов.
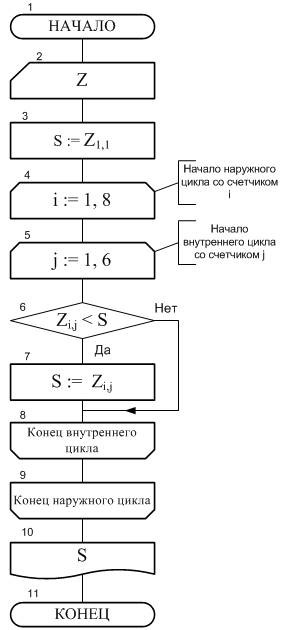
Пример 1. Рассмотрим задачу нахождения наименьшего элемента в двумерном массиве Z размером 8 х 6 .
Блок-схема алгоритма показана на рис. 9. Она включает 11 блоков. После начала работы в блоке 2 массив Z заполняется константами. В блоке 3 новая переменная S получает значение элемента, расположенного в левом верхнем углу массива Z . Далее с помощью вложенных друг в друга цикла будет совершен последовательный проход по всем элементам массива Z и в случаях, когда текущий элемент окажется меньшим S , значение этой переменной будет заменено на значение такого элемента .
Наружный цикл образован блоками 4 — 9, а внутренний блоками 5 — 8. В наружном цикле переменная i сначала примет значение 1, после чего будет выполнено тело этого цикла, которым, как видно из схемы, является внутренний цикл.
Во внутреннем цикле на каждом его шаге переменная j последовательно поменяет свои значения от 1 до 6. При этом текущем шаге будет проведено сравнение элемента, расположенного на пересечении строки i и столбца j , со значением переменной S и, если среди них найдется тот, который меньше S, то S будет заменено значением такого элемента. Проверка условия производится в блоке 6, а замена при выполнении этого условия — в блоке 7.
После завершения работы внутреннего цикла произойдет возврат к заголовку наружного цикла, где значение переменной i увеличится на 1 и станет равным i = 2. Затем вновь выполнится весь внутренний цикл, что соответствует проходу по всем элементам второй строки массива Z.
Таким образом, после завершения наружного цикла будет совершен проход по всем элементам массива и в переменной S будет находиться константа, равная значению наименьшего элемента массива Z.
В блоке 10 будет выведено это значение и затем в блоке 11 алгоритм закончит свою работу.
Рис. 9. Алгоритм нахождения наименьшего элемента в двумерном массиве
9. Вспомогательные алгоритмы
Вспомогательный алгоритм является аналогом компьютерной подпрограммы. Он имеет имя и может иметь параметры, которые называются формальными параметрами. Имя служит для того чтобы отличить такой алгоритм от других алгоритмов, а формальные параметры, которые напоминают переменные математических функций, выполняют роль входных и выходных параметров.
Формальные параметры должны быть выбраны таким образом, чтобы ими был исчерпан весь набор необходимых входных и выходных величин. Нередко один и тот же параметр может оказаться входным и выходным одновременно. Например, на вход такого алгоритма может быть подан массив для обработки, а на выходе процедуры он может предстать в измененном виде как выходной параметр.
Среди вспомогательных алгоритмов различают процедуры и функции . В последнем случае имя служит не только для вызова вспомогательного алгоритма, но и предназначено для определения результата работы алгоритма-функции. То есть имя функции в данном случае выступает в роли ячейки памяти, куда запишется результат после завершения работы такого алгоритма.
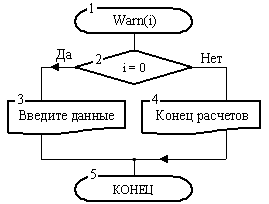
Первый блок схемы рис. 10 в отличие от ранее рассмотренных примеров, где этот блок имел наименование “Начало”, включает имя процедуры Warn и один формальный параметр i .
С помощью этого имени в алгоритме рис. 11 выполняется обращение к этой процедуре. Параметры, которые при вызове алгоритма подставляют на место формальных, называются фактическими параметрами.
Из схемы рис. 11 видно, что если при обращении к процедуре Warn на ее вход подать i = 0, то она в блоке 3 выдаст сообщение «Введите данные». При любом другом i будет выведено сообщение «Конец расчетов». Этим исчерпываются возможности процедура Warn.
Рис. 10. Процедура Warn
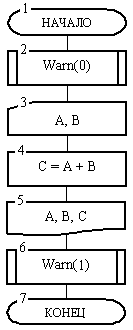
На рис. 11 дана схема головного алгоритма (первый блок имеет наименование «Начало»). Этот алгоритм в блоках 2 и 8 обращается к процедуре Warn (вызывает ее). Опишем последовательность и механизм обработки данных, которые предписаны алгоритмами рис. 10 и 11.
Выполнение алгоритмических действий всегда начинаются с головного алгоритма. Поэтому сначала будет выполнен блок 1 схемы рис. 11. Далее в блоке 2 головной алгоритм выполняет обращение к процедуре Warn при конкретном значении ее аргумента (0).
Теперь управление временно переходит в алгоритм рис. 10 процедуры Warn . Здесь и далее по всей процедуре Warn формальный параметр i заменяется на фактический параметр 0 (нуль) всюду, где он встречается.
Далее обрабатывается блок 2 процедуры, где с учетом сказанного проверяется условие 0 = 0. Результатом проверки станет перевод управления к блоку 3 , в котором выводится сообщение «Введите данные». На этом процедура заканчивается и управление вновь передается в головной алгоритм к блоку 3.
Далее в блоках 3-5 алгоритма рис. 11 выполняются уже понятные действия по вводу, суммированию и выводу переменных. Затем управление передается в блок б, который содержит новое обращение к процедуре Warn с фактическим параметром 1.
Снова управление переключается на схему рис. 10, где вместо формального параметра i всюду записывается фактический параметр – константа 1. Поскольку в блоке 2 условие 1 = 0 не выполнится, то будет выполнен блок 4 и алгоритм выведет сообщение «Конец расчетов».
После этого управление возвращается в головной алгоритм к блоку 7, где и будет окончательно завершен алгоритмический процесс.
Рис. 11. Головной алгоритм
Внешне такой процесс может выглядеть примерно так.
На экран выводится сообщение «Введите данные» и компьютер переходит в режим ожидания ввода двух констант с клавиатуры. Затем после их ввода на экране появляется три константы и надпись «Конец работы».
На первый взгляд может показаться, что процедуры лишь усложняют решение задачи.
Действительно, рассмотренную здесь задачу проще решить одним алгоритмом, не прибегая к составление процедуры. Однако при составлении алгоритма решения сложной задачи очень быстро становится ясно, что без использования процедур обойтись просто невозможно. На практике при решением серьезных алгоритмических задач часто одному программисту не под силу выполнить весь объем работ. Поэтому над ее решением работает обычно коллектив программистов под руководством координатора. Образно говоря, координатор здесь работает как головной алгоритм, а его программисты как процедуры. При этом каждый программист (часто независимо от других) получает от координатора задание по составление процедур определенного назначения. В результате такой организации работы задача получает разрешение.
10. Декомпозиция алгоритма
Под декомпозицией алгоритма понимают разложение его o 6щeй алгоритмической схемы на вспомогательные алгоритмы (процедуры и функции) и головной алгоритм. Напомним, такая задача ставится перед студентом при выполнении курсовой или контрольной работы. Одним из условий, которое должно быть обязательно выполнено, является наличие в работе хотя бы одной процедуры или функции (кроме того, работа должна содержать текст описания всех вспомогательных алгоритмов и головного алгоритма).
Метод, при помощи которого обычно выполняется декомпозиция, достаточно прост. Сначала вычленяют основные этапы предстоящей работы. Наиболее сложные этапы оформляют в виде вспомогательных алгоритмов верхнего уровня. Затем, если необходимо, такие этапы делят на этапы более низкого уровня. Наиболее сложные из них также оформляют вспомогательными алгоритмами и т. д. Следуя методу «от сложного к простому», в конечном итоге получают решение поставленной задачи.
Приведем пример декомпозиции для решения задачи сортировки массива в порядке возрастания его элементов.
Решение задачи декомпозиции состоит из трех основных этапов: 1) ввода данных, 2) сортировки массива и 3) вывода отсортированного массива. Первый и третий этапы вследствие их простоты не нуждаются в декомпозиции, поэтому выполняются в головном алгоритме. Второй этап представляет достаточно сложный и самостоятельный фрагмент алгоритмической работы, поэтому его целесообразно выделить в отдельную процедуру, которой можно дать имя Sort.
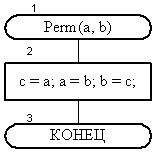
Процедура сортировки требует перестановки значений двух простых переменных. Вспомогательный алгоритм, реализующий эту процедуру, показан на рис. 12. Алгоритм имеет имя Perm ( от английского permutation — перестановка ) и два формальных параметра — переменные a, b. Тело алгоритма состоит из одного символа, где выполняется три оператора присваивания. Сначала оператором c:= a значение ячейки a копируется во вспомогательную переменную c , затем оператором a:= b из ячейки с адресом b производится копирование значения в ячейку с адресом a, последним оператором b:= c из вспомогательной ячейки с адресом c значение копируется в переменную с адресом b . В результате такого кругового копирования содержимое ячеек a и b поменяется местами.
Выполним далее сортировку массива в порядке возрастания его элементов «методом пузырька». Этот метод достаточно прост. Сначала совершают проход по всем соседним парам элементов массива и в случае, если они не отсортированы, то значения элементов всякой такой пары меняют местами. Если была совершена хотя бы одна перестановка, то такую процедуру повторяют до тех пор, пока при проходе по массиву не будет совершено ни одной перестановки. В результате массив будет отсортирован.
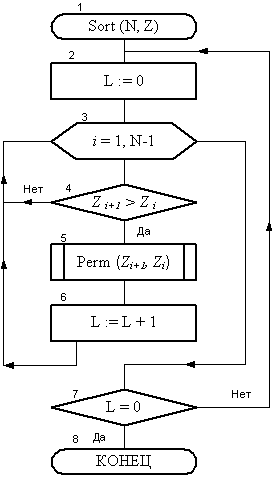
Вспомогательный алгоритм сортировки массива приведен на рис. 13. Алгоритм имеет имя Sort и содержит два формальных параметра : N — длина массива, Z — имя массива, который надлежит отсортировать.
Сортировка производится при помощи двух сложенных друг в друга цикла. Наружный цикл образован блоками 2 — 7 и предназначен для многократного прохода по массиву. Внутри него находится цикл, содержащий блоки 3 — 6. Этот цикл нужен для однократного прохода по всем парам соседних элементов массива с целю перестановки несортированных пар элементов. Переменная L играет роль параметра, по которому можно определить производились ли перестановки при выполнении внутреннего цикла.
Алгоритм работает следующим образом. Сначала в блоке 2 параметр L получает значение 0 (нуль). Далее выполняется цикл блоков 3 — 6. В нем счетчик цикла i будет последовательно принимать значения 1, 2, 3, . N-1. При каждом таком значении счетчика в блоке 4 производится сравнение соседних элементов с номерами i и i+1 . В том случае, если пара не отсортирована, то в блоке 5 путем обращения к вспомогательному алгоритму Perm эта пара будет отсортирована путем перестановки значений этих элементов. После каждой перестановки счетчик перестановок L будет увеличиваться на 1. После прохода по парам элементов на выходе из внутреннего цикла выполнится проверка количества совершенных перестановок. Если перестановок не было ( L = 0 ), то это значит, что массив отсортирован и можно заканчивать работу процедуры сортировки. Если же это не так, то управление предается на блок 2 и процесс сортировки продолжится по той же схеме. Наружный цикл будет выполняться до тех пор, пока при проходе по внутреннему циклу не будет выполнено ни одной перестановки.
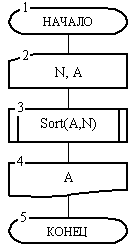
На рис. 14 показан головной алгоритм, который и решает поставленную задачу. Сначала в блоке 2 задается количество N элементов массива и все N ячеек массива A заполняются числами. Затем в блоке 3 происходит вызов вспомогательного алгоритма Sort. В нем на место формального параметра N подставляется фактическое значение параметра N головного алгоритма, а на место формального массива Z подставляется фактический м ассив A . Теперь управление передается в алгоритм Sort, который выполнит сортировку массива A.
После сортировки в блоке 4 головного алгоритма отсортированный массив будет выведен и в блоке 5 алгоритм закончит свою работу.
Рис. 12. Процедура Perm
Рис. 13. Процедура Sort
Рис. 14. Головной алгоритм
В заключение приведем пример алгоритма-функции. Она похожа на вспомогательный алгоритм-процедуру, но в отличие от последней должна в своем теле содержать команду присваивания результата имени функции, т. к. результат после вычислений сохранится в переменной, представленной именем функции.
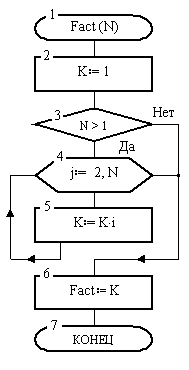
Рассмотрим задачу вычисления факториала числа N! = 1 . 2 . 3 . . . N. Результатом будет одно число, поэтому лучше алгоритм оформить в виде функции .
Б лок — схема алгоритма-функции показана на рис. 15. Переменная К используется для накопления произведения и, поскольку 0! = 1 и1! = 1, то в блоке 2 ей сразу присваивается значение 1. Далее, если N > 1 , то в цикле, образованном блоками 4-5, накапливается искомое произведение и помещается в переменную К. В блоке 6 имя Fact функции получает значение вычисленного произведения из ячейки К. Для процедур действия, размещенного в блоке 6, не может быть, а для функций оно должно быть обязательно, поскольку иначе значение функции на выходе окажется неопределенным.
Обращение к функции в других алгоритмах (головных, процедурах, функциях) производится по ее имени.
При этом оно может входить в состав выражений. В качестве фактических параметров могут быть использованы как переменные, константы, так и целые выражения. Важно только, чтобы фактический параметр был совместим по типу с формальным, который содержится в заголовке описания алгоритма.
Пример использования функции Fact показан на рис. 16. В операторе присваивания используется обращение к функции для N = 6. После передачи этого значения в алгоритм рис. 15 и вычислений внутри него результат будет сначала присвоен имени функции, т. е. переменной Fact, а затем в операторе присваивания — переменной L.
Рис. 15. Функция Fact
Рис. 16. Обращение к функции Fact
Тест на вспомогательный алгоритм
В представленном на рисунке алгоритме
формальные параметры:
x — одномерный массив,
n — его длина,
L — некоторое число.
Если обратиться к алгоритму
при помощи оператора
H := k + Array(a, 5, m) / 3 ,
то при k = 4, m = 11, a = (1, 6, 12, 4, 0)
значением переменной H будет .
Источник
