Алгоритмического способа решения задачи

· широкое внедрение в образовательный процесс информационных технологий и компьютерной техники потребовало существенного изменения традиционных способов обучения и воспитания;

· общая педагогика остается очень теоретической, методика обучения и воспитания — очень практической, поэтому требуется промежуточное звено, позволяющее в действительности связать теорию и практику.

Рассматривая педагогическую технологию в контексте профессионально-педагогической культуры, правомерно выделить в ее структуре и такой элемент, как технология педагогической деятельности, фиксирующий совокупность приемов и способов целостного осуществления педагогического процесса. Введение в научный оборот понятия «технология педагогической деятельности» предполагает построение такой модели, которая основывалась бы на идеях системного, целостного подходов, рассмотрения педагогической деятельности как процесса решения многообразных педагогических задач, являющихся по своей сути задачами социального управления. Технология педагогической деятельности рассматривается через призму решения совокупности педагогических задач по педагогическому анализу, целеполаганию и планированию, организации, оценке и коррекции. Технология педагогической деятельности, таким образом, представляет собой реализацию приемов и способов управления образовательным процессом в школе.

Педагогическая задача, выражая единство цели субъекта деятельности и условий, в которых она решается, должна отвечать ряду требований, для реализации которых и осуществляются педагогические действия как способы решения педагогических задач.

Способы решения задачи могут быть алгоритмическими или квазиалгоритмическими. Алгоритмический способ применяется в том случае, если процедура решения задачи состоит из эффективных операций и не содержит неоднозначно детерминированных разветвлений. Квазиалгоритмический способ решения задачи содержит неоднозначно детерминированные разветвления, определяемые условиями реально поставленной задачи. В педагогической практике преобладают квазиалгоритмические способы решения задач. Высокий уровень решения задач в деятельности педагога обусловлен наличием разнообразных моделей, конструкций решения, зафиксированных в памяти индивида. Часто адекватное решение не находится не потому, что нет «в запасниках» памяти адекватных способов решения, а потому, что учитель (часто начинающий) не видит и не принимает самой ситуации, требующей решения.

Источник

8 базовых алгоритмических задач на собеседованиях

Oct 27, 2019 · 3 min read

Во время собеседования на должность в IT-сфере часто касаются вопросов применения алгоритмов. Наиболее популярными являются алгоритмы поиска и сортировки (строковые алгоритмы, бинарный поиск, алгоритм поиска на графах). Несмотря на кажущуюся простоту, они бывают коварны и трудны в реализации под конкретную задачу. Вот почему важно заранее отработать принцип применения каждого алгоритма, а не полагаться на слепую удачу. Чем лучше вы поймёте схему работы, чем подробнее сможете описать решение данных вам задач, тем выше будут шансы на успешное прохождение собеседования.

Будьте готовы к хитрым вопросам и решению проблем альтернативными способами. Например, часто просят вместо рекурсии разобрать задачу через итеративный алгоритм.

Ре а лизуйте алгоритм бинарного поиска

Бинарный поиск — это алгоритм, следующий парадигме «разделяй и властвуй»: задача разбивается на подзадачи. Этот алгоритм поиска удобен, если нужно найти число в массиве простых чисел или элемент в списке. Самый простой способ решения — при помощи рекурсии.

Важно: бинарный поиск возможен, только если массив данных отсортирован.

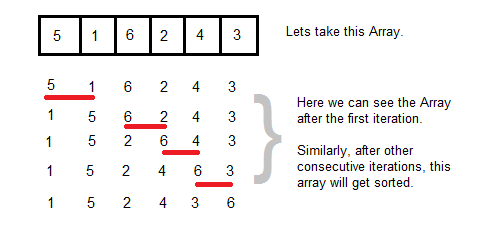
Реализуйте сортировку пузырьком

Во время сортировки пузырьком сравнивают рядом стоящие числа, выстраивая их в порядке убывания или возрастания.

Временная сложность — O(n²), из-за которого алгоритм подходит только для небольшого объёма данных.

Разница между устойчивой и неустойчивой сортировкой

При устойчивой сортировке не меняется относительный порядок сортируемых элементов, имеющих одинаковые ключи, при неустойчивой — меняется. Например, алгоритм быстрой сортировки — неустойчивый, алгоритм сортировки слиянием — устойчивый.

Как поменять местами два значения переменных без третьей переменной?

Еще один вопрос с подвохом, который на самом деле очень прост. Вы можете поменять местами два числа, не прибегая к временной или третьей переменной, если присвоите одной переменной значение суммы двух чисел, а потом вычтите из этой суммы значение для каждой из переменных. Пример:

Как реализуется поразрядная сортировка?

Алгоритм с временной сложностью О(n). Согласно википедии, поразрядная сортировка это алгоритм сортировки, не требующий сравнения. Он обрабатывает данные с целочисленными ключами путём группирования ключей в соответствии с индивидуальными разрядами, которые разделяют ту же позицию и значение.

Как реализовать алгоритм сортировки вставкой?

Принцип схож с сортированием колоды или одежды в шкафу. Каждая карта ложится на свое место, иначе говоря, каждый последующий элемент добавляется на определенную позицию.

Как реализовать сортировку слиянием?

Как в случае с быстрой сортировкой, этот метод относят к группе «разделяй и властвуй». Например, чтобы отсортировать массив чисел, вы его разделите на небольшие части, пока не останется массив в один или ноль отсортированных элементов. Далее следует объединить малые массивы, чтобы получить финальный результат.

Стоит отметить, что в сравнении с быстрой сортировкой данный алгоритм обрабатывает элементы медленнее.

Реализуйте алгоритм быстрой сортировки на предпочитаемом языке программирования

Алгоритм относится к группе «разделяй и властвуй», что предопределяет разделение задачи на подзадачи. То есть, сначала нужно разбить имеющиеся данные на мельчайшие составляющие, массивы из одного элемента (или с нулевым количеством элементов).

Источник

Алгоритмы

Алгоритмы. Разработка алгоритма решения задачи

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.

Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.

При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.

В процессе разработки алгоритма решения задачи можно выделить следующие этапы:

Этап 1 . Математическое описание решения задачи.
Этап 2 . Определение входных и выходных данных.
Этап 3 . Разработка алгоритма решения задачи.

Базовые алгоритмические конструкции

В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:

следование (линейный алгоритм);
ветвление (разветвляющийся алгоритм);
цикл-пока (циклический алгоритм).

Линейные алгоритмы

Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример

ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.

На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:

Этап 1. Математическое описание решения задачи.

Математическим решением задачи является известная формула:

где с-длина гипотенузы, a, b – длины катетов.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.

Этап 3. Разработка алгоритма решения задачи.

На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.

Разветвляющиеся алгоритмы

Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример

ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.

Этап 1. Математическое описание решения задачи.

Из курса математики известно, если x > y, то наибольшее число x, если x y, то переход к шагу 6, иначе к шагу 7.

Вывод информации: число x больше y. Переход к шагу 8.

Вывод информации: число y больше x. Переход к шагу 8.

Конец алгоритма.

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма

В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:

первая: это элементы 1, 2, 3, 4, 8.
вторая: это элементы 1, 2, 3, 5, 6, 8
третья: это элементы 1, 2, 3, 5, 7, 8.

Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.

Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.

Циклические алгоритмы

Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.

При разработке алгоритма циклической структуры выделяют следующие понятия:

параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
начальное и конечное значения параметров цикла;
шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.

Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:

начальные значения цикла;
конечные значения цикла;
шаг цикла.

В тело цикла входят:

многократно повторяющиеся действия для вычисления искомых величин;
подготовка следующего значения параметра цикла;
подготовка других значений, необходимых для повторного выполнения действий в теле цикла.

В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.

Пример

ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.

Этап 1. Математическое описание решения задачи.

Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:

где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.

Этап 2. Определение входных и выходных данных.

Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.

Выходные данные – значение суммы членов последовательности натуральных чисел.

Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.

Подготовка цикла заключается в задании начального и конечного значений параметра цикла.

начальное значение параметра цикла равно 1,
конечное значение параметра цикла равно n,
шаг цикла равен 1.

Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.

Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:

Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.

Этап 3. Разработка алгоритма решения задачи.

Введем обозначения: S – сумма последовательности, i – значение натурального числа.

Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.

Источник

Словесное описание алгоритма	Запись алгоритма на языке блок-схем
Начало алгоритма. Ввод значений длин катетов a и b. Вычисление длины гипотенузы с по формуле Вывод значения длины гипотенузы. Конец алгоритма