Алгоритмический способ измерения информации это

Алгоритмическое измерение информации [2]

Был предложен в 1965 году академиком А.Н. Колмогоровым. Алгоритмическая сложность некоторой последовательности данных определяется как минимальная длина вычислительного алгоритма, который мог бы воспроизвести заданную последовательность.

Например: слово 000000 – простое, слово 01010101 – более сложное, а слово, в котором 0 и 1 выбираются экспериментально при бросании монеты (1 – орел, 0 – решка), еще сложнее.

Компьютерная программа, печатающая первое слово, совсем простая; для получение второго слова нужна более сложная программа, которая будет печатать символ, противоположный предыдущему. Случайная последовательность, не обладающая никакими закономерностями, может быть напечатана программой, в которой каждый очередной символ будет печататься отдельным оператором. То есть длина такой программы будет близка к длине самой последовательности. Следовательно, любому сообщению можно приписать количественную характеристику, отражающую размер программы, которая позволяет ее воспроизвести.

Алгоритмический подход к измерению количества информации, в силу ряда объективных причин, не нашел широкого практического применения.

Единицы измерения информации:

В качестве единицы информации условились принять один бит (англ. bit — binary digit — двоичная цифра).

Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа «орел»—»решка», «чет»—»нечет» и т.п.).

В вычислительной технике битом называют наименьшую «порцию» памяти компьютера, необходимую для хранения одного из двух знаков «0» и «1», используемых для внутримашинного представления данных и команд.

Бит — слишком мелкая единица измерения. На практике чаще применяется более крупная единица — байт, равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2 8 ).

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет не двоичная (бит), а десятичная (дит) единица информации.

Таким образом, основание логарифма в формуле Хартли не имеет принципиального значения и определяет только масштаб или единицу измерения. В зависимости от основания логарифма применяют следующие единицы измерения:

Наты – основание логарифма равно е. I= lnN

Диты – основание логарифма равно 10. I= lgN

2.6.2. Основные соотношения между единицами измерения сообщений:

1 бит (binary digit – двоичное число) = 0 или 1,

1 Килобайт (Кбайт) = 1024 байт = 2 10 байт,

1 Мегабайт (Мбайт) = 1024 Кбайт = 2 20 байт,

1 Гигабайт (Гбайт) = 1024 Мбайт = 2 30 байт.

В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:

1 Терабайт (Тбайт) = 1024 Гбайт = 2 40 байт,

1 Петабайт (Пбайт) = 1024 Тбайт = 2 50 байт

1 Эксабайт (1Э) = 1024 Пбайт = 2 60 байт,

Источник

Методы измерения информации

Как и любое физическое вещество информация имеет свои количественные характеристики. В современной информатике приняты следующие методы измерения информации:

Объемный метод измерения характеризуется количеством символов, содержащихся в конкретном сообщении. В вычислительной технике вся информация, независимо от ее природы (текст, число, изображение и т.д.), представляется в двоичной форме записи, т.е. состоящей из различных комбинаций двух символов 0 и 1. Один такой символ в вычислительной технике называется битом, совокупность восьми таких символов называется байтом, а большое количество символов, которыми оперирует ЭВМ, называется словом.

Энтропийный метод измерения информации используется в теории информации и кодирования. Он основывается на мере неопределенности появления некоторой совокупности событий и выражается вероятностью появления этих событий. Количество информации в сообщении при энтропийном методе оценки определяется тем, насколько уменьшается эта мера после получения сообщения. В теории информации используется следующая количественная мера:

где Э – энтропия;

m – число возможных равновероятных событий.

В случае, когда энтропия зависит не только от числа равновероятных событий выбора, но и от вероятности возможного выбора элемента информации К. Шеннон предложил следующую форму оценки энтропии:

где Р_i – вероятность возможного выбора i-го элемента информации.

Тогда среднее количество информации при m числе выборке с вероятностью Рi каждой выборки определится выражением:

Алгоритмическая оценка информации характеризуется сложностью (размером) алгоритма (программы), которая позволяет ее произвести. На разных машинах и разных языках программирования такая оценка может быть разной. Поэтому задаются некоторой вычислительной машиной (например, элементарной машиной Тьюринга), а предлагаемая количественная оценка информации определяется сложностью слова, как минимальное число внутренних состояний машины, требуемой для его воспроизведения.

Структурная схема машины Тьюринга приведена на рисунке 2.2.

Рисунок 2.2 – Структурная схема машины Тьюринга

На рисунке 2.2 обозначено:

УУ – управляющее устройство;

СГ – считывающая головка;

Лента – источник информации бесконечная лента.

Управляющее устройство УУ определяет положение считывающей головки СГ <q_i>. В каждой ячейке ленты записан символ <a_i>. Таким образом, состояние машины <s_i> определится выражением:

Следующее перемещение ленты задается параметром <p_i>. Тогда новое состояние машины определится следующим образом:

Таким образом, полное состояние машины Тьюринга можно задать, определив множества Q, A, P. Алгоритм определения состояния машины Тьюринга является единицей алгоритмического метода оценки информации.

Источник

Информация[4]

Информация — фундаментальное, первичное понятие информатики.

Информация [1] (от лат. Informatio — разъяснение, осведомление, изложение) — отражение внешнего мира с помощью знаков и сигналов.

В быту под информацией понимают сведения об окружающем мире и протекающих в нем процессах, воспринимаемые человеком или специальными устройствами

В технике информация — сообщения, передаваемые в виде последовательности знаков или сигналов

В теории информации под информацией понимают только сведения, уменьшающие существовавшую до их появления неопределенность (Информация — это снятая неопределенность. (К. Шеннон))

В кибернетике (теории управления) информация — та часть знаний, которая используется для ориентирования, активного действия, управления, т. е. в целях сохранения, совершенствования, развития системы

В семантической теории — сведения, обладающие новизной

В документалистике — все, что в так или иначе зафиксировано в знаковой форме в виде документов.

По отношению к окружающей среде информация бывает

• входная (получается от окружающей среды);
• выходная (выдается в окружающую среду);
• внутренняя (внутрисистемная).

По отношению к конкретной задаче, проблеме

• исходная (существовавшая до начала обработки);
• промежуточная (от начала до завершения обработки);
• результирующая (после завершения обработки).

• постоянная (никогда не изменяемая);
• переменная (изменяемая в процессе работы);
• смешанная (условно-постоянная или условно-переменная).

Прочие классификации информации: по полноте, по принадлежности (территории, физическому или юридическому лицу и т.д.), по доступу, по предметной области, по характеру использования (коммерческая, справочная, учебная и т.п.) и др

Ноосфера (от греч. noos — мысль, разум и sphaira — сфера) Сфера деятельности человеческого разума. Современное состояние биосферы, возникшее в процессе деятельности человека. (Понятие впервые введено В. И. Вернандским)

Основные свойства информации [1],[4]

• полнота ( >);
• объективность;
• достоверность;
• актуальность (необходимость, своевременность);
• интерпретируемость (понятность);
• кодируемость и экономичность кодировки;
• избыточность;
• защищенность и помехоустойчивость.

Методы получения и использования информации

• Эмпирические методы
  • наблюдение;
  • сравнение;
  • измерение;
  • эксперимент.

• Теоретические методы
  • идеализация (мысленное исследование упрощенных, не существующих в действительности подобий изучаемых систем);
  • формализация (описание системы с помощью формальных языков, например, математических формул, и исследование полученной модели);
  • аксиоматизация (получение знаний на основе принятия некоторых аксиом);
  • виртуализация (исследование системы в искусственно созданной среде, обстановке, ситуации).

• Эмпирико-теоретические методы
  • абстрагирование (установление общих свойств объектов путем отбрасывания несущественных деталей);
  • анализ (разбиение системы на подсистемы);
  • синтез (объединение подсистем в систему);
  • индукция (переход от частного к общему);
  • дедукция (переход от общего к частному);
  • моделирование, макетирование;
  • визуализация и др.

2 Носители информации [1]

Информация всегда связана с материальным носителем

Носитель информации — среда для записи и хранения информации

Сигнал — способ передачи информации. Это физический процесс, какая-либо характеристика которого изменяется во времени. Сигнал может быть дискретным или аналоговым.

Аналоговый сигнал — сигнал, непрерывно (плавно) изменяющийся во времени

Дискретный сигнал может принимать конечное число значений, скачком переходя от одного такого значения к другому

Для работы с аналоговыми сигналами цифровыми методами выполняют их дискретизацию

3 Измерение информации

3.1 Объемный способ измерения информации [2]

Технический способ измерения количества информации (или, точнее, информационного объема сообщения) основан на подсчета количества символов, из которых образовано сообщение. При этом не учитывается смысловое содержание сообщения. Например, многократное повторение одного и того же текста не несет новой информации, однако в результате занимает больший объем памяти, требует большего времени для передачи и т.п. Поэтому этот способ удобен в технических расчетах

За 1 бит в этом случае принимается один двоичный символ в сообщении

3.2 Алгоритмическое измерение информации [2]

А. Н. Колмогоров (1965 г.): Алгоритмическая сложность некоторой последовательности данных определяется как минимальная длина вычислительного алгоритма, который мог бы воспроизвести заданную последовательность

3.3 Вероятностный подход к измерению количества информации [4]

3.3.1 Мера Р. Хартли

Американским инженером Р. Хартли в 1928 г. получена формула для определения количества информации, получаемой при реализации одного из N равновероятных состояний

где a — основание системы,
N — количество равновозможных состояний,
P — вероятность реализации состояния.

При a = e единица измерения называется >, при a = 2 — >, при a = 10 — >

Пример 1 ДНК человека можно представить как некоторое слово четырехбуквенного алфавита, где буквы соответствуют нуклеотидам 1 .
Определим, какое количество информации содержит ДНК, если она состоит примерно из 1.5×10 23 нуклеотидов.
Так как алфавит — четырехбуквенный, каждый символ слова несет log₂4 = 2 бита информации. Следовательно ДНК в целом позволяет хранить 3×10 23 бит или около 3×10 10 Терабайт информации.

3.3.2 Задачи с > ответами [3]

Задача 1 Имеется колода из 32 игральных карт (без шестерок). Задумана одна из карт. Какое наименьшее число вопросов нужно задать, чтобы угадать задуманную карту, если на вопросы даются ответы > и >?

Задача 2 Задумано целое число от нуля до ста. Какое наименьшее число вопросов нужно задать, чтобы угадать это число?

Задача 3 Задумано некоторое число. Известно, что отгадать его можно, задав 7 вопросов. Оцените это число.

Задача 4 Имеется 26 монет, одна из которых — фальшивая (более легкая). Каким образом за 3 взвешивания определить фальшивую монету?

Задача 5 Имеется 41 монета, из них одна — фальшивая. Как при помощи двух взвешиваний определить, тяжелее фальшивая монета настоящей или легче?

3.3.3 Мера К. Шеннона

Американский математик и инженер К. Шеннон в 1948 г. получил формулу для расчета количества информации, содержащейся в системе, обладающей произвольным набором неравновероятных (в общем случае) состояний

I = — pilog2pi,

(2)

где n — число возможных состояний системы, p_i — вероятность i-го состояния (причем 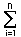p_i = 1)

Чем меньше вероятность наступления события, тем большую информацию это событие несет

Задача 6 Используя данные Примера refdnk, определите суммарный объем информации в человеческом теле, считая его состоящим из примерно 10 13 клеток.

Задача 7 Ресурсы человеческого мозга позволяют обрабатывать информацию со скоростью около 16 бит/с. Какое количество информации перерабатывает человек в течение жизни (принять среднюю продолжительность жизни за 60 лет).

Задача 8 Некоторая система может находиться в четырех состояниях: в первом — с вероятностью 0.1, во втором и третьем — 0.25, в четвертом — 0.4. Чему равно количество информации в ситеме?

Задача 9 Система может принимать 128 различных равновероятных состояний. Каково количество информации в системе?

Задача 10 Определите количество информации, которое несет каждая буква в русском тексте. Какое количество букв в алфавите нужно было бы для передачи такого же количества информации, если бы их появление в слове было равновероятным

Буква	Частота	Буква	Частота	Буква	Частота
о	0.090	к	0.028	ь (ъ), б	0.014
е (ё)	0.072	м	0.026	ч	0.013
а, и	0.062	д	0.025	й	0.012
т, н	0.053	п	0.023	х	0.009
с	0.045	у	0.021	ж, ю, ш	0.006
р	0.040	я	0.018	ц, щ, э	0.003
в	0.035	ы, з	0.016	ф	0.002

Литература

Дополнительный материал:

Примечания:

1 В зависимости от входящего в состав нуклеотида гетероциклического основания: аденина, гуанина, цитозина или тимина

Источник