Алгоритм решения задач графическим способом

Решение задач линейного программирования графическим методом

Описание метода

Если в задаче линейного программирования имеется только две переменные, то ее можно решить графическим методом.

Рассмотрим задачу линейного программирования с двумя переменными и :
(1.1) ;
(1.2)
Здесь , есть произвольные числа. Задача может быть как на нахождение максимума (max), так и на нахождение минимума (min). В системе ограничений могут присутствовать как знаки , так и знаки .

Построение области допустимых решений

Графический метод решения задачи (1) следующий.
Вначале мы проводим оси координат и и выбираем масштаб. Каждое из неравенств системы ограничений (1.2) определяет полуплоскость, ограниченную соответствующей прямой.

Так, первое неравенство
(1.2.1)
определяет полуплоскость, ограниченную прямой . С одной стороны от этой прямой , а с другой стороны . На самой прямой . Чтобы узнать, с какой стороны выполняется неравенство (1.2.1), мы выбираем произвольную точку, не лежащую на прямой. Далее подставляем координаты этой точки в (1.2.1). Если неравенство выполняется, то полуплоскость содержит выбранную точку. Если неравенство не выполняется, то полуплоскость расположена с другой стороны (не содержит выбранную точку). Заштриховываем полуплоскость, для которой выполняется неравенство (1.2.1).

Тоже самое выполняем для остальных неравенств системы (1.2). Так мы получим заштрихованных полуплоскостей. Точки области допустимых решений удовлетворяют всем неравенствам (1.2). Поэтому, графически, область допустимых решений (ОДР) является пересечением всех построенных полуплоскостей. Заштриховываем ОДР. Она представляет собой выпуклый многоугольник, грани которого принадлежат построенным прямым. Также ОДР может быть неограниченной выпуклой фигурой, отрезком, лучом или прямой.

Может возникнуть и такой случай, что полуплоскости не содержат общих точек. Тогда областью допустимых решений является пустое множество. Такая задача решений не имеет.

Можно упростить метод. Можно не заштриховывать каждую полуплоскость, а вначале построить все прямые
(2)
Далее выбрать произвольную точку, не принадлежащую ни одной из этих прямых. Подставить координаты этой точки в систему неравенств (1.2). Если все неравенства выполняются, то область допустимых решений ограничена построенными прямыми и включает в себя выбранную точку. Заштриховываем область допустимых решений по границам прямых так, чтобы оно включало в себя выбранную точку.

Если хотя бы одно неравенство не выполняется, то выбираем другую точку. И так далее, пока не будет найдены одна точка, координаты которой удовлетворяют системе (1.2).

Нахождение экстремума целевой функции

Итак, мы имеем заштрихованную область допустимых решений (ОДР). Она ограничена ломаной, состоящей из отрезков и лучей, принадлежащих построенным прямым (2). ОДР всегда является выпуклым множеством. Оно может быть как ограниченным множеством, так и не ограниченным вдоль некоторых направлений.

Теперь мы можем искать экстремум целевой функции
(1.1) .

Для этого выбираем любое число и строим прямую
(3) .
Для удобства дальнейшего изложения считаем, что эта прямая проходит через ОДР. На этой прямой целевая функция постоянна и равна . такая прямая называется линией уровня функции . Эта прямая разбивает плоскость на две полуплоскости. На одной полуплоскости
.
На другой полуплоскости
.
То есть с одной стороны от прямой (3) целевая функция возрастает. И чем дальше мы отодвинем точку от прямой (3), тем больше будет значение . С другой стороны от прямой (3) целевая функция убывает. И чем дальше мы отодвинем точку от прямой (3) в другую сторону, тем меньше будет значение . Если мы проведем прямую, параллельную прямой (3), то новая прямая также будет линией уровня целевой функции, но с другим значением .

Таким образом, чтобы найти максимальное значение целевой функции, надо провести прямую, параллельную прямой (3), максимально удаленную от нее в сторону возрастания значений , и проходящую хотя бы через одну точку ОДР. Чтобы найти минимальное значение целевой функции, надо провести прямую, параллельную прямой (3) и максимально удаленную от нее в сторону убывания значений , и проходящую хотя бы через одну точку ОДР.

Если ОДР неограниченна, то может возникнуть случай, когда такую прямую провести нельзя. То есть как бы мы ни удаляли прямую от линии уровня (3) в сторону возрастания (убывания) , то прямая всегда будет проходить через ОДР. В этом случае может быть сколь угодно большим (малым). Поэтому максимального (минимального) значения нет. Задача решений не имеет.

Рассмотрим случай, когда крайняя прямая, параллельная произвольной прямой вида (3), проходит через одну вершину многоугольника ОДР. Из графика определяем координаты этой вершины. Тогда максимальное (минимальное) значение целевой функции определяется по формуле:
.
Решением задачи является
.

Также может встретиться случай, когда прямая параллельна одной из граней ОДР. Тогда прямая проходит через две вершины многоугольника ОДР. Определяем координаты и этих вершин. Для определения максимального (минимального) значения целевой функции, можно использовать координаты любой из этих вершин:
.
Задача имеет бесконечно много решений. Решением является любая точка, расположенная на отрезке между точками и , включая сами точки и .

Пример решения задачи линейного программирования графическим методом

Фирма выпускает платья двух моделей А и В. При этом используется ткань трех видов. На изготовление одного платья модели А требуется 2 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. На изготовление одного платья модели В требуется 3 м ткани первого вида, 1 м ткани второго вида, 2 м ткани третьего вида. Запасы ткани первого вида составляют 21 м, второго вида — 10 м, третьего вида — 16 м. Выпуск одного изделия типа А приносит доход 400 ден. ед., одного изделия типа В — 300 ден. ед.

Составить план производства, обеспечивающий фирме наибольший доход. Задачу решить графическим методом.

Пусть переменные и означают количество произведенных платьев моделей А и В, соответственно. Тогда количество израсходованной ткани первого вида составит:
(м)
Количество израсходованной ткани второго вида составит:
(м)
Количество израсходованной ткани третьего вида составит:
(м)
Поскольку произведенное количество платьев не может быть отрицательным, то
и .
Доход от произведенных платьев составит:
(ден. ед.)

Тогда экономико-математическая модель задачи имеет вид:

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 7) и (10,5; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 10) и (10; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (8; 0).

Прямые и являются осями координат.

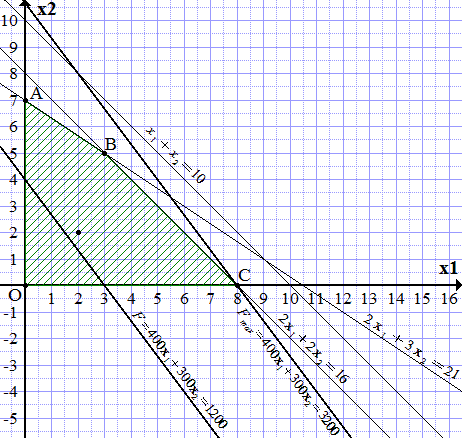
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (2; 2) попала в заштрихованную часть. Получаем четырехугольник OABC.

Строим произвольную линию уровня целевой функции, например,
(П1.1) .
При .
При .
Проводим прямую через точки (0; 4) и (3; 0).

Далее замечаем, что поскольку коэффициенты при и целевой функции положительны (400 и 300), то она возрастает при увеличении и . Проводим прямую, параллельную прямой (П1.1), максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку четырехугольника OABC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

.
То есть, для получения наибольшего дохода, необходимо изготовить 8 платьев модели А. Доход при этом составит 3200 ден. ед.

Пример 2

Решить задачу линейного программирования графическим методом.

Решаем графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 6) и (6; 0).

Строим прямую .
Отсюда .
При .
При .
Проводим прямую через точки (3; 0) и (7; 2).

Строим прямую .
Строим прямую (ось абсцисс).

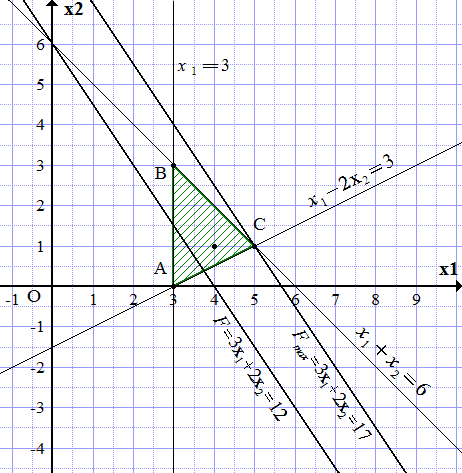
Область допустимых решений (ОДР) ограничена построенными прямыми. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область по границам построенных прямых, чтобы точка (4; 1) попала в заштрихованную часть. Получаем треугольник ABC.

Строим произвольную линию уровня целевой функции, например,
.
При .
При .
Проводим прямую линию уровня через точки (0; 6) и (4; 0).
Поскольку целевая функция увеличивается при увеличении и , то проводим прямую, параллельную линии уровня и максимально удаленную от нее в сторону возрастания , и проходящую хотя бы через одну точку треугольника АВC. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.

Пример отсутствия решения

Решить графически задачу линейного программирования. Найти максимальное и минимальное значение целевой функции.

Решаем задачу графическим методом.
Проводим оси координат и .

Строим прямую .
При .
При .
Проводим прямую через точки (0; 8) и (2,667; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (0; 3) и (6; 0).

Строим прямую .
При .
При .
Проводим прямую через точки (3; 0) и (6; 3).

Прямые и являются осями координат.

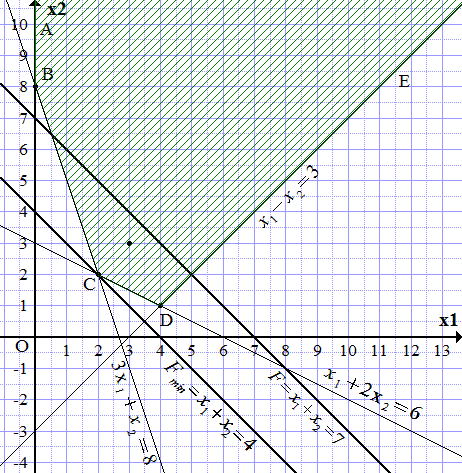
Область допустимых решений (ОДР) ограничена построенными прямыми и осями координат. Чтобы узнать, с какой стороны, замечаем, что точка принадлежит ОДР, поскольку удовлетворяет системе неравенств:

Заштриховываем область, чтобы точка (3; 3) попала в заштрихованную часть. Получаем неограниченную область, ограниченную ломаной ABCDE.

Строим произвольную линию уровня целевой функции, например,
(П3.1) .
При .
При .
Проводим прямую через точки (0; 7) и (7; 0).
Поскольку коэффициенты при и положительны, то возрастает при увеличении и .

Чтобы найти максимум, нужно провести параллельную прямую, максимально удаленную в сторону возрастания , и проходящую хотя бы через одну точку области ABCDE. Однако, поскольку область неограниченна со стороны больших значений и , то такую прямую провести нельзя. Какую бы прямую мы не провели, всегда найдутся точки области, более удаленные в сторону увеличения и . Поэтому максимума не существует. можно сделать сколь угодно большой.

Ищем минимум. Проводим прямую, параллельную прямой (П3.1) и максимально удаленную от нее в сторону убывания , и проходящую хотя бы через одну точку области ABCDE. Такая прямая проходит через точку C. Из построения определяем ее координаты.
.
Минимальное значение целевой функции:

Максимального значения не существует.
Минимальное значение
.

Автор: Олег Одинцов . Опубликовано: 08-08-2016

Источник

Презентация и разработка урока «Графический способ решения задач»

Выбранный для просмотра документ Открытый урок 19.02.15.pptx

Описание презентации по отдельным слайдам:

Дисциплина: ЕН 01 Математика Специальность : Садово-парковое и ландшафтное строительство Преподаватель: Есенеева Эльвира Самигулловна Пермь 2015 Государственноепрофессиональное образовательноеучреждение «Пермский агропромышленный техникум»

«Если поручить двум людям, один из которых хорошо разбирается в математике, выполнение любой незнакомой им работы, то результат всегда будет следующим: знающий математику сделает ее лучше». Гуго Штейнгауз (польский математик , 1887 – 1972)

Тема: Графический способ решения задач линейного программирования

Цель: Закрепить навыки решения задач линейного программирования с применением графического метода

План занятия 1. Повторение . 2. Практическая работа. 3. Подведение итогов. 4. Демонстрация решения задач ЛП с помощью ИКТ. 5. Домашнее задание.

Линейное программирование – наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи Линейная функция Целевая функция Ограничения Система ограничений Математическое выражение целевой функции и ее ограничений называется математической моделью задачи

Основные этапы построения математических моделей Определение цели, т.е чего хотят добиться решая поставленную задачу. Определение параметров модели, т.е. заранее известных фиксированных факторов, на значения которых исследователь не влияет. Формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели. Значения управляющих переменных и являются решениями задачи. Определение области допустимых решений, т.е. тех ограничений, которым должны удовлетворять управляющие переменные. Выявление неизвестных факторов, т.е. величин, которые могут изменяться случайным и неопределенным образом. Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.е. формирование целевой функции, называемой также критерием эффективности или критерием оптимальности задачи.

Повторение Решение линейных неравенств с двумя переменными

Решение линейных неравенств с двумя переменными Повторение

Алгоритм решения задач ЛП графическим методом Составить математическую модель задачи Найти область допустимых решений системы ограничений задачи. Построить вектор С. Провести линию уровня L0, которая перпендикулярна С. 5. Линию уровня перемещаем по направлению вектора С для задач на максимум и в направлении противоположном С, для задач на минимум.

Графический способ решения задач линейного программирования Задача Некоторая фирма выпускает 2 набора удобрений для газонов: смесь А и смесь В . В таблице приведено содержание в смесях азотных, фосфорных и калийных удобрений. Пакет А стоит 8 у.е, смеси В – 6 у.е. Для некоторого газона требуется не менее 7,38 кг азотных, не менее 4,1 кг фосфорных и не менее 3,28 кг калийных удобрений. Определите сколько пакетов каждого вида следует купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость покупки. Смеси Содержание удобрений (кг) азотных фосфорных калийных А 1,64 0,82 0,41 В 1,23 0,82 1,64

Решение: Обозначим через: х – число наборов смеси А, у — число наборов смеси В Математическая модель задачи: Целевая функция: Система ограничений задачи:

A B D C Решение задачи графическим способом А(0;6), В(3;2). Стоимость 36 у.е.

Исследование области допустимых решений системы ограничений задачи ЛП

Решить графически систему: ОДР: пустое множество

Решить графически систему: ОДР: Открытое множество

Решить графически систему: ОДР: многоугольник

Решить графически систему: 1 решение — точка

ПРАКТИЧЕСКОЕ ЗАДАНИЕ Цель работы: Решить задачу линейного программирования (найти оптимальное решение при заданных условиях).  Резерв времени: на выполнение практического задания – 10 минут на представление результатов работы – 2 минуты Задания 1. Ознакомиться с условием задачи. 2. Составить математическую модель задачи : — целевую функцию; — систему ограничений. 3. Изобразить область допустимых решений (ОДР) задачи. (Масштаб — за единицу 2 клетки — для наглядности при демонстрировании на документ – камере). 4. Найти решение задачи. — если решением задачи является точка пересечения двух прямых, проверить координаты этой точки решая систему уравнений, составленную из уравнений этих прямых. 5. Презентовать задачу. P.S. При необходимости использовать опорные конспекты и справочный материал.

Задача для гр №1. При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса заданы в таблице: Прибыль от реализации одной единицы товара 1-го вида 2 у.е, 2-го вида – 3 у.е. требуется найти оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль. ПРАКТИЧЕСКОЕ ЗАДАНИЕ Ресурсы Норма затрат ресурсов Общее количество ресурсов 1-го вида 2-го вида 1 2 2 12 2 1 2 8 3 4 0 16 4 0 4 12

A B C D O Решение задачи (гр .1) С(4;2) Стоимость -14 у.е.

Задача для гр №2. При подкормке посевов необходимо ввести на 1 га почвы не менее 10 единиц органического вещества А, не менее 24 единиц вещества В и не менее 16 единиц вещества С. Фермер закупает комбинированные удобрения двух видов 1 и 2. В таблице приведены содержание количества единиц вещества в 1 кг каждого вида удобрений и цена 1 кг удобрений: Определить потребность фермера в удобрениях 1 и 2 вида на 1 га посевной площади при минимальных затратах на их приобретение. Вещества Содержание органическихвеществ в 1 кг удобрения 1-го вида 2-го вида А 2 5 В 12 3 С 4 4 Цена 1 кг удобрения,ву.е. 5 2

A B C D Проверка (задача для гр .2) Затраты — 12 у.е.

Выпуск одной единицы веса удобрения А приносит доход 6 у.е., вида В – 4 у.е. Составить план производства, обеспечивающий фирме наибольший доход. Задача для гр №3 Фирма выпускает удобрения двух видов: А и В. При этом используется сырье 4-ех видов. Расход сырья каждого вида на изготовление единицы веса удобрения и ежедневные запасы сырья заданы в таблице: Выпуск одной единицы веса удобрения А приносит доход 6 у.е., вида В – 4 у.е. Составить план производства, обеспечивающий фирме наибольший доход. Удобрения Сырье 1-го вида 2 – го вида 3 – его вида 4 – го вида А 2 1 0 2 В 3 0 1 1 Ежедневные запасы сырья, ед. 21 4 6 10

A B C E D O Проверка (задача для гр .3) С (2,25; 5,5) Доход 35,5 у.е.

Задача для гр №4. Для подкормки саженцев фундука садово – огородническому хозяйству требуется еженедельно не менее 7 единиц вещества А, не менее 4 единиц вещества В и не менее 16 единиц вещества С. Нужно закупить 2 вида удобрений. В таблице приведено содержание в единице веса 1 кг удобрений каждого из этих веществ. Определить сколько единиц веса каждого вида удобрения следует купить, чтобы обеспечить эффективную подкормку фундука и минимизировать стоимость покупки. Изделия Удобрения 1 вида 2 вида А 5 1 В 1 1 С 2 7 Стоимость 1 ед. веса удобрения 6 4

A B C D Проверка (задача для гр. 4) Доход 17,5 у.е.

Домашнее задание 1. По данным представлен- ным в таблице составить профессионально–ориен-тированную задачу; данные для целевой функции предложить самостоятельно) 2. Найти максимум целевой функции при ограничениях: Продукт Химические добавки, мг/л X Y Z A B 4 5 2 1 3 1

Выбранный для просмотра документ графический способ.doc.docx

Государственное бюджетное профессиональное образовательное учреждение

«Пермский агропромышленный техникум»

Дисциплина: Математика с элементами высшей (база среднее общее (полное) образование)

Преподаватель: Есенеева Эльвира Самигулловна

ПЛАН УЧЕБНОГО ЗАНЯТИЯ

Тема занятия: Графический способ решения задач линейного программирования

— формировать целостное представление о графическом способе решения задач линейного программирования

— развивать умения по осуществлению поиска и использованию информации, необходимой для эффективного выполнения профессиональных задач на оптимизацию

— развивать навыки коммуникационного взаимодействия, умение выстраивать логические связи, презентационные умения;

— воспитывать чувство ответственности за порученное дело, чувство коллективизма

Тип занятия: усвоение новых знаний

Форма организации деятельности студентов: фронтальная, групповая.

— организации и осуществления учебных действий: лекция с использованием слайд-презентации, беседа с постановкой проблемных вопросов , демонстрация процесса решения задач; решение практических задач профессиональной направленности

— методы организации деятельности и формирования опыта: погружение в профессиональную среду , работа с опорными конспектами, самоконтроль, работа в микрогруппах;

— методы стимулирования и мотивации деятельности: соревнование, установление связи учебного материала с прежним опытом студента и с будущим видом профессиональной деятельности, создание ситуации успеха

— методы контроля: экспресс-опрос, экспертное заключение.

Использованные педагогические технологии: технология обучения в математике на основе решения задач, деятельностный подход в обучении

Метапредметные связи: ОП 05 . Экономика организации; МДК 02.03. Маркетинг ландшафтных услуг; ЕН Информационные технологии в профессиональной деятельности

Методическое обеспечение занятия: опорные конспекты, слайд-презентация, лист экспертной оценки, методические рекомендации по выполнению практического задания

Техническое, информационное и материальное обеспечение занятия: компьютер, мультимедиапроектор, лазерная ручка-указка, экран, программный пакет « MathCAD », угольник, линейка.

Источник