Алгоритм евклида способ вычисления

Алгоритм Евклида

Алгоритм Евклида — это способ нахождения наибольшего общего делителя (НОД) двух целых чисел. Оригинальная версия алгоритма, когда НОД находится вычитанием, была открыта Евклидом (III в. до н. э). В настоящее время чаще при вычислении НОД алгоритмом Евклида используют деление, так как данный метод эффективнее.

Вычисление НОД делением

Наибольший общий делитель пары чисел – это самое большое число, которое нацело делит оба числа пары. Пусть требуется вычислить НОД для чисел 108 и 72. Алгоритм вычисления делением будет таковым:

1. Разделим большее число (делимое) на меньшее (делитель): 108 / 72 = 1, остаток 36.
2. Поскольку остаток не был равен нулю, то сделаем делитель делимым, а остаток – делителем: 72 / 36 = 2, остаток 0.
3. Когда остаток равен нулю, то делитель является искомым НОД для пары заданных чисел. То есть НОД(108, 72) = 36. Действительно, 108 / 36 = 3 и 72 / 36 = 2.

В данном алгоритме деление повторяется до тех пор, пока остаток не станет равным нулю. Когда он таковым становится, НОДом является делитель последнего деления. Например, требуется найти НОД(106, 16):

1. 106 / 16 = 6, остаток 10
2. 16 / 10 = 1, остаток 6
3. 10 / 6 = 1, остаток 4
4. 6 / 4 = 1, остаток 2
5. 4 / 2 = 2, остаток 0
6. НОД(106, 16) = 2

Вычисление НОД вычитанием

При нахождении НОД вычитанием также требуется достичь нуля. Алгоритм схож с методом деления, только здесь на каждом следующем этапе вычитаемым и уменьшаемым становятся вычитаемое и разность из предыдущего шага. При этом всегда из большего числа вычитается меньшее. Данная разновидность алгоритма подходит только для положительных целых чисел.

Пусть требуется найти НОД(108, 72):

1. 108 — 72 = 36
2. 72 — 36 = 36
3. 36 — 36 = 0
4. НОД(108, 72) = 36

Найдем НОД(44, 60):

1. 60 — 44 = 16
2. 44 — 16 = 28
3. 28 — 16 = 12
4. 16 — 12 = 4
5. 12 — 4 = 8
6. 8 — 4 = 4
7. 4 — 4 = 0
8. НОД(44, 60) = 4

Данный алгоритм иногда описывают по-другому. Вычитание заканчивают раньше, на шаге, когда одно число нацело делит другое. То есть комбинируют вычитание с проверкой делимости. Тогда нахождение НОД для 44 и 60 будет выглядеть так:

1. Делит ли 44 нацело 60? Нет. 60 — 44 = 16.
2. Делит ли 16 нацело 44? Нет. 44 — 16 = 28.
3. Делит ли 16 нацело 28? Нет. 28 — 16 = 12.
4. Делит ли 12 нацело 16? Нет. 16 — 12 = 4.
5. Делит ли 4 нацело 12? Да. Значит, НОД(44, 60) = 4.

Обратите внимание, НОДом является не частное, а делитель. Если в примере мы разделим 12 на 4, то получим частное 3. Но это не НОД.

Доказательство алгоритма Евклида

Примем во внимание факт, что если одно натуральное число из пары нацело делит другое, то их НОД будет равен меньшему из них. Записать это можно так:

если a / b нацело, то НОД(a, b) = b. Например, НОД(15, 5) = 5.

Таким образом, если в конечном итоге мы приходим к паре чисел, одно из которых делит нацело другое, то меньшее будет для обоих наибольшим общим делителем. Именно такая пара чисел ищется алгоритмом Евклида: одно число нацело делит другое.

Второй факт. Требуется доказать, что если одно число больше другого, то их наибольший общий делитель равен наибольшему общему делителю для меньшего числа из пары, и разнице большего и меньшего чисел. Это можно записать так:

Если последовательно уменьшать a и b, то рано или поздно придем к такому значению меньшего из них, которое нацело делит большее. Меньшее в такой паре будет наибольшим общим делителем для исходной пары натуральных чисел. В этом и заключается алгоритм Евклида.

Источник

Как найти НОД двух чисел по алгоритму Евклида

Что такое алгоритм Евклида

Алгоритм Евклида — один из наиболее ранних численных алгоритмов в истории. Название было дано в честь греческого математика Евклида, который впервые дал ему описание в книгах «Начала». Изначально назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль. Сегодня чаще используется взятие остатка от деления вместо вычитания, но суть метода сохранилась.

Алгоритм Евклида — это алгоритм, основная функция которого заключается в поиске наибольшего общего делителя (НОД) для двух целых чисел.

Простейшим случаем применения данного алгоритма является поиск наибольшего общего делителя для пары положительных целых чисел. Евклид, автор этого метода, предполагал его использование только для натуральных чисел и геометрических величин. Но позже алгоритм был обобщен и для других групп математических объектов, что привело к появлению такого понятия, как евклидово кольцо.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Понятие НОД

Аббревиатура НОД расшифровывается как «наибольший общий делитель».

Наибольший общий делитель — делитель, который делит без остатка два числа, при этом сам делится без остатка на любой другой делитель исходных двух чисел. То есть это самое большое число, на которое без остатка можно разделить пару чисел, для которых подбирается НОД.

Основная суть алгоритма Евклида

Суть алгоритма заключается в построении ряда следующего вида (при условии, что a больше b):

В нем каждое последующее число — это остаток от деления двух предыдущих, ряд заканчивается, когда остаток от деления становится равным 0 — при условии использования деления.

В нем каждое последующее число является результатом вычитания двух предыдущих, ряд заканчивается, когда частное становится равным 0 — при условии использования вычитания.

Последовательность нахождения НОД при помощи деления:

1. Большее число делится на меньшее.
2. Если результат деления:

• без остатка, то меньшее число и есть НОД;
• с остатком, тогда большее число заменяется на остаток.

1. Переход к пункту 1.

60 / 36 = 1 (остаток 24)

36 / 24 = 1 (остаток 12)

24 / 12 = 2 (остаток 0)

НОД для 60 и 36 равен 12 (делитель).

Последовательность нахождения НОД при помощи вычитания:

1. Из большего числа вычитается меньшее.
2. Если результат вычитания:

• равен 0, то числа равны друг другу и являются НОД;
• не равен 0, в таком случае большее число заменяется на результат вычитания.

1. Переход к пункту 1.

НОД для 60 и 36 равен 12 (уменьшаемое, вычитаемое)

Примеры решения задач с алгоритмом Евклида

Найти наибольший общий делитель для чисел 128 и 96.

128 / 96 = 1 (остаток 32)

Найти наибольший общий делитель для чисел 37 и 17.

37 / 17 = 2 (остаток 3)

17 / 3 = 5 (остаток 2)

3 / 2 = 1 (остаток 1)

2 / 1 = 2 (остаток 0)

Числа 37 и 17 являются простыми, соответственно, их НОД — единица. Совет: перед вычислениями проверяйте таблицу простых чисел.

Источник

Алгоритм Евклида

Из Википедии — свободной энциклопедии

Алгори́тм Евкли́да — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел (или общей меры двух отрезков). Алгоритм назван в честь греческого математика Евклида (III век до н. э.), который впервые описал его в VII [1] и X [2] книгах «Начал». Это один из старейших численных алгоритмов, используемых в наше время [3] .

В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары. Евклид предложил алгоритм только для натуральных чисел и геометрических величин (длин, площадей, объёмов). Однако в XIX веке он был обобщён на другие типы математических объектов, включая целые числа Гаусса и полиномы от одной переменной. Это привело к появлению в современной общей алгебре такого понятия, как евклидово кольцо. Позже алгоритм Евклида был обобщён на другие математические структуры, такие как узлы и многомерные полиномы.

Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA [4] , широко распространённого в электронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений [5] , при построении непрерывных дробей [6] , в методе Штурма [7] . Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например таких как теорема Лагранжа о сумме четырёх квадратов [8] и основная теорема арифметики [9] .

Источник

Алгоритмы. Алгоритм Евклида. Часть 1

Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.

Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.

Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.

Переборный алгоритм

Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.

Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.

Алгоритм Евклида «с вычитанием»

Пусть a и b — целые числа, тогда верны следующие утверждения:

1. Все общие делители пары a и b являются также общими делителями пары a — b, b;
2. И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
3. НОД(A, B) = НОД(A — B, B), если A > B;
4. НОД(A, 0) = A.

1. Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
2. Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
3. Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
4. Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.

Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.

Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.

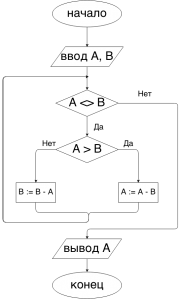
Блок — схема алгоритма Евклида «с вычитанием»

Программа

Алгоритм Евклида с «делением»

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).

Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.

На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.

Источник

Алгоритм Евклида

Алгоритм Евклида — это способ нахождения наибольшего общего делителя (НОД) двух целых чисел. Оригинальная версия алгоритма, когда НОД находится вычитанием, была открыта Евклидом (III в. до н. э). В настоящее время чаще при вычислении НОД алгоритмом Евклида используют деление, так как данный метод эффективнее.

Вычисление НОД делением

Наибольший общий делитель пары чисел – это самое большое число, которое нацело делит оба числа пары. Пусть требуется вычислить НОД для чисел 108 и 72. Алгоритм вычисления делением будет таковым:

1. Разделим большее число (делимое) на меньшее (делитель): 108 / 72 = 1, остаток 36.
2. Поскольку остаток не был равен нулю, то сделаем делитель делимым, а остаток – делителем: 72 / 36 = 2, остаток 0.
3. Когда остаток равен нулю, то делитель является искомым НОД для пары заданных чисел. То есть НОД(108, 72) = 36. Действительно, 108 / 36 = 3 и 72 / 36 = 2.

В данном алгоритме деление повторяется до тех пор, пока остаток не станет равным нулю. Когда он таковым становится, НОДом является делитель последнего деления. Например, требуется найти НОД(106, 16):

1. 106 / 16 = 6, остаток 10
2. 16 / 10 = 1, остаток 6
3. 10 / 6 = 1, остаток 4
4. 6 / 4 = 1, остаток 2
5. 4 / 2 = 2, остаток 0
6. НОД(106, 16) = 2

Вычисление НОД вычитанием

При нахождении НОД вычитанием также требуется достичь нуля. Алгоритм схож с методом деления, только здесь на каждом следующем этапе вычитаемым и уменьшаемым становятся вычитаемое и разность из предыдущего шага. При этом всегда из большего числа вычитается меньшее. Данная разновидность алгоритма подходит только для положительных целых чисел.

Пусть требуется найти НОД(108, 72):

1. 108 — 72 = 36
2. 72 — 36 = 36
3. 36 — 36 = 0
4. НОД(108, 72) = 36

Найдем НОД(44, 60):

1. 60 — 44 = 16
2. 44 — 16 = 28
3. 28 — 16 = 12
4. 16 — 12 = 4
5. 12 — 4 = 8
6. 8 — 4 = 4
7. 4 — 4 = 0
8. НОД(44, 60) = 4

Данный алгоритм иногда описывают по-другому. Вычитание заканчивают раньше, на шаге, когда одно число нацело делит другое. То есть комбинируют вычитание с проверкой делимости. Тогда нахождение НОД для 44 и 60 будет выглядеть так:

1. Делит ли 44 нацело 60? Нет. 60 — 44 = 16.
2. Делит ли 16 нацело 44? Нет. 44 — 16 = 28.
3. Делит ли 16 нацело 28? Нет. 28 — 16 = 12.
4. Делит ли 12 нацело 16? Нет. 16 — 12 = 4.
5. Делит ли 4 нацело 12? Да. Значит, НОД(44, 60) = 4.

Обратите внимание, НОДом является не частное, а делитель. Если в примере мы разделим 12 на 4, то получим частное 3. Но это не НОД.

Доказательство алгоритма Евклида

Примем во внимание факт, что если одно натуральное число из пары нацело делит другое, то их НОД будет равен меньшему из них. Записать это можно так:

если a / b нацело, то НОД(a, b) = b. Например, НОД(15, 5) = 5.

Таким образом, если в конечном итоге мы приходим к паре чисел, одно из которых делит нацело другое, то меньшее будет для обоих наибольшим общим делителем. Именно такая пара чисел ищется алгоритмом Евклида: одно число нацело делит другое.

Второй факт. Требуется доказать, что если одно число больше другого, то их наибольший общий делитель равен наибольшему общему делителю для меньшего числа из пары, и разнице большего и меньшего чисел. Это можно записать так:

Если последовательно уменьшать a и b, то рано или поздно придем к такому значению меньшего из них, которое нацело делит большее. Меньшее в такой паре будет наибольшим общим делителем для исходной пары натуральных чисел. В этом и заключается алгоритм Евклида.

Источник