- Нахождение НОД по алгоритму Евклида и с помощью разложения на простые множители.
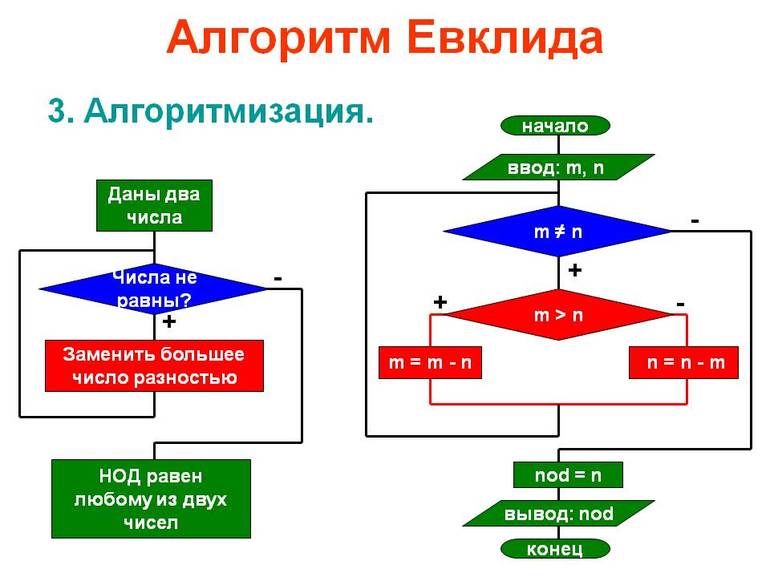
- Алгоритм Евклида для нахождения НОД
- Нахождение НОД с помощью разложения чисел на простые множители
- Нахождение НОД трех и большего количества чисел
- Нахождение НОД отрицательных чисел
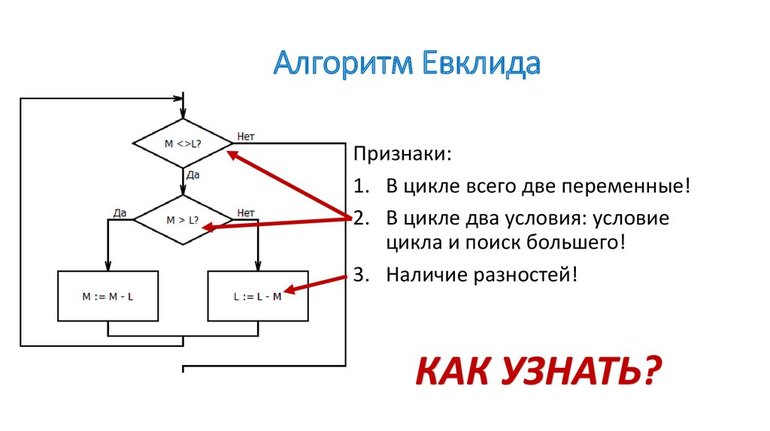
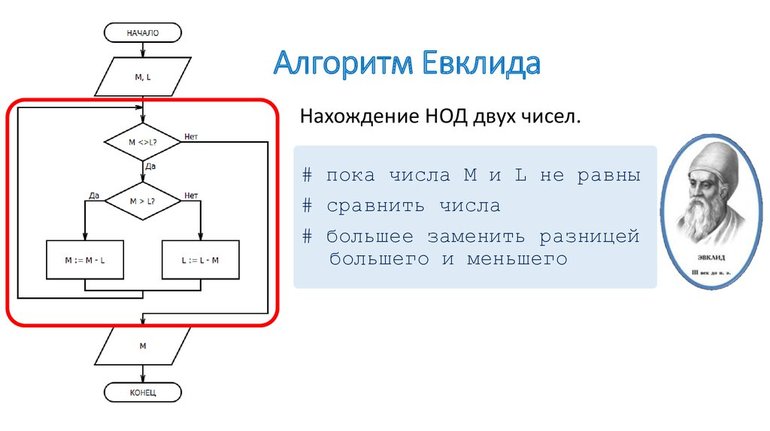
- Как найти НОД двух чисел по алгоритму Евклида
- Что такое алгоритм Евклида
- Понятие НОД
- Основная суть алгоритма Евклида
- Последовательность нахождения НОД при помощи деления:
- Последовательность нахождения НОД при помощи вычитания:
- Примеры решения задач с алгоритмом Евклида
- Алгоритм Евклида — формулы, правила и примеры решения задач
- Общие сведения
- Описание и доказательство алгоритма
- Применение в математике
- Различные вариации
- Пример решения
Нахождение НОД по алгоритму Евклида и с помощью разложения на простые множители.
Эта статья про нахождение наибольшего общего делителя (НОД) двух и большего количества чисел. Сначала рассмотрим алгоритм Евклида, он позволяет находить НОД двух чисел. После этого остановимся на методе, позволяющем вычислять НОД чисел как произведение их общих простых множителей. Дальше разберемся с нахождением наибольшего общего делителя трех и большего количества чисел, а также приведем примеры вычисления НОД отрицательных чисел.
Навигация по странице.
Алгоритм Евклида для нахождения НОД
В статье наибольший общий делитель (НОД), определение, примеры, свойства НОД мы сформулировали и доказали алгоритм Евклида. Алгоритм Евклида является универсальным способом, позволяющим вычислять наибольший общий делитель двух положительных целых чисел.
Напомним суть алгоритма Евклида. Для нахождения наибольшего общего делителя двух чисел a и b ( a и b – целые положительные числа, причем a больше или равно b ) последовательно выполняется деление с остатком, которое дает ряд равенств вида 
Деление заканчивается, когда rk+1=0 , при этом rk=НОД(a, b) .
Рассмотрим примеры нахождения НОД по алгоритму Евклида.
Найдите наибольший общий делитель чисел 64 и 48 .
Воспользуемся алгоритмом Евклида. В этом примере a=64 , b=48 .
Делим 64 на 48 , получаем 64:48=1 (ост. 16) (при необходимости смотрите правила и примеры деления с остатком), что можно записать в виде равенства 64=48·1+16 , то есть, q1=1 , r1=16 .
Теперь делим b на r1 , то есть, 48 делим на 16 , получаем 48:16=3 , откуда имеем 48=16·3 . Здесь q2=3 , а r2=0 , так как 48 делится на 16 без остатка. Мы получили r2=0 , поэтому это был последний шаг алгоритма Евклида, и r1=16 является искомым наибольшим общим делителем чисел 64 и 48 .
Покажем решение еще одного примера, но теперь обойдемся без подробных пояснений шагов алгоритма Евклида.
Чему равен НОД чисел 111 и 432 ?
Из свойств наибольшего общего делителя мы знаем, что НОД(111, 432)=НОД(432, 111) . Воспользуемся алгоритмом Евклида для нахождения НОД(432, 111) .
Разделив 432 на 111 , получаем равенство 432=111·3+99 .
На следующем шаге делим 111 на 99 , имеем 111=99·1+12 .
Деление 99 на 12 дает равенство 99=12·8+3 .
А 12 на 3 делится без остатка и 12=3·4 . Поэтому это последний шаг алгоритма Евклида, и НОД(432, 111)=3 , следовательно, и искомый наибольший общий делитель чисел 111 и 432 равен 3 .
Для закрепления материала найдем с помощью алгоритма Евклида наибольший общий делитель чисел 661 и 113 .
Найдите НОД(661, 113) по алгоритму Евклида.
Выполняем деление: 661=113·5+96 ; 113=96·1+17 ; 96=17·5+11 ; 17=11·1+6 ; 11=6·1+5 ; 6=5·1+1 , наконец, 5=1·5 . Таким образом, НОД(661, 113)=1 , то есть, 661 и 113 – взаимно простые числа.
Заметим, что если бы мы с самого начала обратились к таблице простых чисел, то выяснили бы, что числа 661 и 113 – простые, откуда можно было бы сразу сказать, что их наибольший общий делитель равен 1 .
Нахождение НОД с помощью разложения чисел на простые множители
Рассмотрим еще один способ нахождения НОД. Наибольший общий делитель может быть найден по разложениям чисел на простые множители. Сформулируем правило: НОД двух целых положительных чисел a и b равен произведению всех общих простых множителей, находящихся в разложениях чисел a и b на простые множители.
Приведем пример для пояснения правила нахождения НОД. Пусть нам известны разложения чисел 220 и 600 на простые множители, они имеют вид 220=2·2·5·11 и 600=2·2·2·3·5·5 . Общими простыми множителями, участвующими в разложении чисел 220 и 600 , являются 2 , 2 и 5 . Следовательно, НОД(220, 600)=2·2·5=20 .
Таким образом, если разложить числа a и b на простые множители и найти произведение всех их общих множителей, то этим будет найден наибольший общий делитель чисел a и b .
Рассмотрим пример нахождения НОД по озвученному правилу.
Найдите наибольший общий делитель чисел 72 и 96 .
Разложим на простые множители числа 72 и 96 :
То есть, 72=2·2·2·3·3 и 96=2·2·2·2·2·3 . Общими простыми множителями являются 2 , 2 , 2 и 3 . Таким образом, НОД(72, 96)=2·2·2·3=24 .
В заключение этого пункта заметим, что справедливость приведенного правила нахождения НОД следует из свойства наибольшего общего делителя, которое утверждает, что НОД(m·a1, m·b1)=m·НОД(a1, b1) , где m – любое целое положительное число.
Нахождение НОД трех и большего количества чисел
Нахождение наибольшего общего делителя трех и большего количества чисел может быть сведено к последовательному нахождению НОД двух чисел. Мы об этом упоминали, при изучении свойств НОД. Там мы сформулировали и доказали теорему: наибольший общий делитель нескольких чисел a1, a2, …, ak равен числу dk , которое находится при последовательном вычислении НОД(a1, a2)=d2 , НОД(d2, a3)=d3 , НОД(d3, a4)=d4 , …, НОД(dk-1, ak)=dk .
Давайте разберемся, как выглядит процесс нахождения НОД нескольких чисел, рассмотрев решение примера.
Найдите наибольший общий делитель четырех чисел 78 , 294 , 570 и 36 .
Сначала по алгоритму Евклида определим наибольший общий делитель d2 двух первых чисел 78 и 294 . При делении получаем равенства 294=78·3+60 ; 78=60·1+18 ; 60=18·3+6 и 18=6·3 . Таким образом, d2=НОД(78, 294)=6 .
Теперь вычислим d3=НОД(d2, a3)=НОД(6, 570) . Опять применим алгоритм Евклида: 570=6·95 , следовательно, d3=НОД(6, 570)=6 .
Осталось вычислить d4=НОД(d3, a4)=НОД(6, 36) . Так как 36 делится на 6 , то d4=НОД(6, 36)=6 .
Таким образом, наибольший общий делитель четырех данных чисел равен d4=6 , то есть, НОД(78, 294, 570, 36)=6 .
НОД(78, 294, 570, 36)=6 .
Разложение чисел на простые множители также позволяет вычислять НОД трех и большего количества чисел. В этом случае наибольший общий делитель находится как произведение всех общих простых множителей данных чисел.
Вычислите НОД чисел из предыдущего примера, используя их разложения на простые множители.
Разложим числа 78 , 294 , 570 и 36 на простые множители, получаем 78=2·3·13 , 294=2·3·7·7 , 570=2·3·5·19 , 36=2·2·3·3 . Общими простыми множителями всех данных четырех чисел являются числа 2 и 3 . Следовательно, НОД(78, 294, 570, 36)=2·3=6 .
НОД(78, 294, 570, 36)=6 .
Нахождение НОД отрицательных чисел
Если одно, несколько или все числа, наибольший делитель которых нужно найти, являются отрицательными числами, то их НОД равен наибольшему общему делителю модулей этих чисел. Это связано с тем, что противоположные числа a и −a имеют одинаковые делители, о чем мы говорили при изучении свойств делимости.
Найдите НОД отрицательных целых чисел −231 и −140 .
Модуль числа −231 равен 231 , а модуль числа −140 равен 140 , и НОД(−231, −140)=НОД(231, 140) . Алгоритм Евклида дает нам следующие равенства: 231=140·1+91 ; 140=91·1+49 ; 91=49·1+42 ; 49=42·1+7 и 42=7·6 . Следовательно, НОД(231, 140)=7 . Тогда искомый наибольший общий делитель отрицательных чисел −231 и −140 равен 7 .
Определите НОД трех чисел −585 , 81 и −189 .
При нахождении наибольшего общего делителя отрицательные числа можно заменить их абсолютными величинами, то есть, НОД(−585, 81, −189)= НОД(585, 81, 189) . Разложения чисел 585 , 81 и 189 на простые множители имеют соответственно вид 585=3·3·5·13 , 81=3·3·3·3 и 189=3·3·3·7 . Общими простыми множителями этих трех чисел являются 3 и 3 . Тогда НОД(585, 81, 189)=3·3=9 , следовательно, НОД(−585, 81, −189)=9 .
Источник
Как найти НОД двух чисел по алгоритму Евклида
Что такое алгоритм Евклида
Алгоритм Евклида — один из наиболее ранних численных алгоритмов в истории. Название было дано в честь греческого математика Евклида, который впервые дал ему описание в книгах «Начала». Изначально назывался «взаимным вычитанием», так как его принцип заключался в последовательном вычитании из большего числа меньшего, пока в результате не получится ноль. Сегодня чаще используется взятие остатка от деления вместо вычитания, но суть метода сохранилась.
Алгоритм Евклида — это алгоритм, основная функция которого заключается в поиске наибольшего общего делителя (НОД) для двух целых чисел.
Простейшим случаем применения данного алгоритма является поиск наибольшего общего делителя для пары положительных целых чисел. Евклид, автор этого метода, предполагал его использование только для натуральных чисел и геометрических величин. Но позже алгоритм был обобщен и для других групп математических объектов, что привело к появлению такого понятия, как евклидово кольцо.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Понятие НОД
Аббревиатура НОД расшифровывается как «наибольший общий делитель».
Наибольший общий делитель — делитель, который делит без остатка два числа, при этом сам делится без остатка на любой другой делитель исходных двух чисел. То есть это самое большое число, на которое без остатка можно разделить пару чисел, для которых подбирается НОД.
Основная суть алгоритма Евклида
Суть алгоритма заключается в построении ряда следующего вида (при условии, что a больше b):
В нем каждое последующее число — это остаток от деления двух предыдущих, ряд заканчивается, когда остаток от деления становится равным 0 — при условии использования деления.
В нем каждое последующее число является результатом вычитания двух предыдущих, ряд заканчивается, когда частное становится равным 0 — при условии использования вычитания.
Последовательность нахождения НОД при помощи деления:
- Большее число делится на меньшее.
- Если результат деления:
- без остатка, то меньшее число и есть НОД;
- с остатком, тогда большее число заменяется на остаток.
- Переход к пункту 1.
60 / 36 = 1 (остаток 24)
36 / 24 = 1 (остаток 12)
24 / 12 = 2 (остаток 0)
НОД для 60 и 36 равен 12 (делитель).
Последовательность нахождения НОД при помощи вычитания:
- Из большего числа вычитается меньшее.
- Если результат вычитания:
- равен 0, то числа равны друг другу и являются НОД;
- не равен 0, в таком случае большее число заменяется на результат вычитания.
- Переход к пункту 1.
НОД для 60 и 36 равен 12 (уменьшаемое, вычитаемое)
Примеры решения задач с алгоритмом Евклида
Найти наибольший общий делитель для чисел 128 и 96.
128 / 96 = 1 (остаток 32)
Найти наибольший общий делитель для чисел 37 и 17.
37 / 17 = 2 (остаток 3)
17 / 3 = 5 (остаток 2)
3 / 2 = 1 (остаток 1)
2 / 1 = 2 (остаток 0)
Числа 37 и 17 являются простыми, соответственно, их НОД — единица. Совет: перед вычислениями проверяйте таблицу простых чисел.
Источник
Алгоритм Евклида — формулы, правила и примеры решения задач
Общие сведения
Математики называют алгоритм Евклида для нахождения НОД взаимным вычитанием. Древнегреческий ученый впервые применил его для двух целых чисел. Позднее это новшество использовалось для нахождения наибольшей величины делителя двух однородных величин (отрезков, земельных участков и т. д. ). Он является старым и эффективным численным алгоритмом. Его применение следует объяснять для пары положительных целых чисел, хотя можно использовать правило и для десятичных дробей. Его изучают в старших классах.
Суть алгоритма заключается в формировании новой пары чисел из меньшего и разницы между большим и меньшим элементом. Процесс, состоящий из арифметических операций, повторяется до тех пор, пока числа не будут равны друг другу. Первоначально инструкция создавалась для натуральных чисел и геометрических величин. Однако в XIX веке ее расширили и стали применять для других объектов: целых чисел Гаусса и многочленов с одной переменной (полиномов). Направление, получившееся в математике, специалисты стали называть евклидовым кольцом. Позднее его доработали и стали применять для узлов и многомерных полиномов.
Алгоритм является основой для криптографического шифрования с открытым ключом, который распространен в электронной коммерции для защиты программных продуктов от злоумышленников. Его применяют для решения уравнений Диофанта, построения дробей непрерывного типа, доказательств утверждений (основная теорема арифметики и теорема Лагранжа о сумме 4 квадратов).
Описание и доказательство алгоритма
Для целых чисел алгоритм состоит из соотношений, количество которых равно числу элементов. Если предположить, что а и b являются целыми и неравными нулю значениями, то для них выполняется соотношение a > b > R1 > … > Rn. Величинами R с определенными индексами являются остатки от деления а на некоторое значение Q1 и b на Q2. Описывается процесс такими формулами:
- а = b * q0 + R1.
- b = R1 * q1 + R2.
- R1 = R2 * Q2 + R3.
- Rn-1 = Rn * Qn.
На последнем этапе не должно быть остатка. Для отрезков применяется геометрический алгоритм. Чтобы найти наибольший общий отрезок, нужно из большего вычесть меньший, а затем заменить первый их разностью. Операцию следует завершить при равенстве двух отрезков. Реализуется данный алгоритм при помощи циркуля и линейки. Для доказательства алгоритма Евклида следует взять пару чисел f и g, для которых можно привести такие утверждения:
- Делители f и g — общие делители (f — g) и g.
- Делители (f — g) и g — общие делители f и g.
- Когда f > g, тогда НОД (f, g) = НОД (f — g, g).
- НОД (f, 0) = f.
Для доказательства следует ввести новую переменную z. Она является общим делителем для f и g. Кроме того, разность f — g также делится на z. Из предположения f = z * k и g = z * s следует, что f — g = z * k — z * s = z * (k — s). Иными словами, z — общий множитель для f — g. Из соотношения можно доказать, что z делит не только разность, но и сумму: f — g + g = f. Следовательно, z — общий делитель для f и g.
На основании полученных вычислений можно сделать вывод, что z для f и g совпадает с (f — g) и g. Если одно из чисел имеет нулевое значение, то НОД равен другому числу, поскольку 0 делится на любое число.
Следует отметить, что методика для нескольких чисел (трех и более) аналогичная. В этом случае нужно брать не одну разность, а две, в которой будет присутствовать минимальное число. Данный алгоритм применяется в построении программного обеспечения. Однако перед написанием кода следует сначала составить блок-схему. Она позволит избежать ошибок, а также внимательно сосредоточиться на проекте.
Применение в математике
Одним из примеров алгоритма Евклида считается соотношение Безу (лема или тождество). Его суть заключается в представлении НОД в форме линейной комбинации с некоторыми коэффициентами целого типа. Лема имеет следующую формулировку: для целых чисел f и g (хотя бы одно из них не равно 0) существуют некоторые коэффициенты целого типа, для которых справедливо соотношение НОД (f, g) = m * f + n * g, где m и n — коэффициенты Безу.
Тождество справедливо и для натуральных чисел. У него такая же формулировка, только слово «целых» заменяется на «натуральных». Кроме того, существует расширенный алгоритм Евклида:
- R1 = f + g * (-Q0).
- R2 = g — R1 * Q1 = f * (-Q1) + g * (1 + Q1 * Q0).
- Для целых w и z: НОД (f, g) = Rn = f * w + g * z.
Еще одним примером использования алгоритма считаются цепные дроби. Пусть f и g — числитель и знаменатель соответственно. Любая дробь такого типа может быть представлена следующим образом: f / g = [Q0;Q1,Q2,…, Qn]. Без Qn она равна отношению коэффициентов Безу w / z, результат которого нужно брать с отрицательным знаком, т. е. [Q0;Q1,Q2,…, Qn-1] = — w / z. Следовательно, равенства могут иметь такое представление:
- f / g = Q0 + R0 / b.
- b / R0 = Q1 + R1 / R0.
- R0 / R1 = Q2 + R2 / R1.
- (Rn-2) / (Rn-1) = Qn.
Если обратить внимание, то можно понять закономерность: последний элемент правой части равен обратной величине левой части последующего тождества. В результате этого можно объединить две формулы: f / g = Q0 + 1 / [Q1 + (R1/R0)]. Третья применяется для замены знаменателя: f / g = Q0 + 1 / [Q1 + (1 / (Q2 + (R2/R1)))]. Следовательно, можно записать цепную дробь в таком виде: f / g = Q0 + 1 / [Q1 + (1 / (Q2 + … + 1 / Qn))].
Алгоритм применяется и для решения диофантовых уравнений. Диофантовым является уравнение с целыми коэффициентами и одной или несколькими переменными, решение которого сводится к нахождению только целых корней. Решений у него может быть много. Примером простейшего считается обыкновенное линейное с двумя переменными Ах + Ву = С, где А и В — некоторые коэффициенты. Переменными величинами являются х и у. Решается оно следующим образом:
- Находится коэффициент D: D = НОД (А, В).
- При помощи расширенного алгоритма Евклида следует найти некоторые коэффициенты w, z: А * w + B * z = D.
- Получаются такие соотношения (x = w, y = z) при D = С: С = Q * D, х = Q * w и y = Q * z.
- Частное решение: Ах + Ву = А * (Q * w) + B * (Q * z) = Q * (A * w + B * z) = Q * D = C.
Если у уравнения всего один корень, то C кратно D. Данное утверждение следует из соотношения, в котором D делит А, В и всю левую сторону, а значит, должно делить правую на С.
Различные вариации
Кольцо является алгебраическим выражением или структурой, в которой применяются операции сложения (обратимого) и умножения эквивалентные соответствующим действиям над некоторыми числами. Примером считается обобщенные множества целых, дробных и комплексных чисел. Более сложный пример — различные функции с элементами кольца. Если к данному множеству применима лема Евклида, то его называют Евклидовым кольцом. К ним относятся кольца целых чисел и многочленов.
Для многочлена вида Z[g] от одной неизвестной g над некоторым полем (функцией) Z определена операция деления. Последняя выполняется только с остатком. Если применить к нему правило Евклида, то получится последовательность остатков в виде полиномов. Для примера следует разобрать такую задачу: пусть cont (w) является НОД для коэффициентов f (w) из полинома Z[g]. При делении f (w) на cont (w) образуется примитивная часть многочлена primpart (f (w)). Необходимо найти НОД Р1 (g) и Р2 (g). Если числа являются целыми, то в этом случае верны такие тождества:
Следовательно, поиск НОД для двух многочленов нужно свести к поиску НОД примитивных полиномов. Для примитивных полиномов Р1 (g) и Р2 (g), принадлежащих Z[g], выполняется такое соотношение между их степенями: deg (Р1 (g)) = m и deg (Р2 (g)) = n (m > n). Деление с остатком осуществляется по псевдоделимости, поскольку иногда выполнить первую процедуру невозможно.
В результате этого вводят специальный алгоритм для псевдоделения, результатом которого является псевдоостаток. Его обозначают «prem». Формула операции псевдоделения имеет такой вид с учетом псевдочастного Q (g) и псевдоостатка R (g): [lc (P2 (g))^(m-n+1)] * P1 (g) = P2 (g) * Q (g) + R2 (g) при deg (R (g)) = deg (P2) = n2. На основании полученных результатов лема Евклида состоит из таких пунктов:
- Найти НОД: НОД<сont (Р1 (g)), сont (Р2 (g))>.
- Расчет примитивных частей: [P1 (g)]’ = primpart (P1 (g)) и [P2 (g)]’ = primpart (P2 (g)).
- Последовательность псевдоостатков полиномного типа: [P1 (g)]’, [P2 (g)]’, [P3 (g)]’ = prem ([P1 (g)]’, [P2 (g)]’), [P4 (g)]’ = prem ([P2 (g)]’, [P3 (g)]’),…, [Pn (g)]’ = prem ([(Pn-2)(g)]’, [(Pn-1)(g)]’).
- Возвратить результат: если deg (Pn (g)) = 0, то вернуть НОД<сont (Р1 (g)), сont (Р2 (g))>. Иначе — выражение в первом пункте нужно умножить на primpart (Pn (g)).
Существует еще одна разновидность алгоритма. Она называется ускоренной. Ее суть заключается в применении понятия симметричного остатка: Ri = Ri-2 * (mod [Ri-1]). Для данного выражения должно выполняться такое условие: -[Ri-1 / 2] 0 и g > 0, должно выполняться такое неравенство с числами Фибоначчи Fn+2 и Fn+1 соответственно: f >= Fn+2 и g >= Fn+1. Доказывается данное утверждение при помощи математической индукции. Если предположить, что N = 1, то остаток отношения f / g эквивалентен 0.
Наименьшими значениями являются f = 2 и g = 1 (F2 и F3 соответственно). Предположим, что результат для значений на промежутке от N до М — 1. Первый шаг c M шагами записывается таким образом: f = Q0 * g + R0. Следовательно, выполнение алгоритма для чисел g и R0 (g > R0) требует (М — 1) шагов.
В результате этого получаются два нестрогих неравенства g >= Fm+1 и R0 >= Fm. Из выражения следует, что f = Q0 * g + R0 >= g + R0 >=Fm+1 + Fm = Fm+2. Данное доказательство было выполнено в 1844 году математиком Г. Ламе. Оно является главным элементом теории сложности вычислений. Формулировка данного утверждения следующая: при нахождении НОД f и g в результате деления с некоторым остатком число операций по алгоритму Евклида не превосходит 5.
Пример решения
Специалисты рекомендуют закрепить теоретические знания решением различных упражнений. Необходимо разобрать применение алгоритма на примере нахождения НОД (1071,462). Для этого следует действовать по такой инструкции, позволяющей решить простым способом задачу:
- Выполнить операцию разности до получения остатка: 1071 — 462 — 462 + 147 = 1071 — 2 * 462 + 147 (Q0 = 2, R0 = 147).
- От 462 отнять 147 до получения результата, который меньше 147: 462 — 147 — 147 — 147 + 21 = 462 — 3 * 147 + 21 (Q1 = 3, R1 = 21).
- Анализ пары чисел 147 и 21: 147 — 21 — 21 — 21 — 21 — 21 — 21 — 21 + 0 (Q2 = 7, R2 = 0).
- Определение результата: НОД (1071,462) = 21.
На третьем шаге алгоритм заканчивается, поскольку остаток отсутствует, т. е. R2 = 0. В написании программ применяется такой же принцип. Если даны три числа, то методика решения усложняется. Для этой цели применяется специальный онлайн-калькулятор.
Таким образом, алгоритм Евклида помогает за незначительное время найти НОД двух и более чисел.
Источник