Алгебраический способ теорема пифагора

Алгебраическое доказательство теоремы Пифагора

Теорема Пифагора формулируется следующим образом: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

С 2 =А 2 + В 2 , /1/

где: С — гипотенуза;

Существуют прямоугольные треугольники, у которых стороны А, В и С выражаются целыми числами. Такие числа называются пифагоровыми.

Рассматривая уравнение теоремы Пифагора как алгебраическое уравнение, докажем, что существует бесконечное количество прямоугольных треугольников, в которых их стороны выражаются целыми числами или, что одно и тоже, уравнение /1/ имеет бесконечное количество решений в целых числах.

Суть теоремы Пифагора не изменится, если уравнение /1/ запишем следующим образом:

Для доказательства теоремы Пифагора методами элементарной алгебры используем два известные в математике метода решения алгебраических уравнений: метод решения параметрических уравнений и метод замены переменных.

Уравнение /2/ рассматриваем как параметрическое уравнение с параметром A и переменными B и С. Уравнение /2/ в соответствии с известной зависимостью для разности квадратов двух чисел запишем в виде:

Используя метод замены переменных, обозначим:

Из уравнения /4/ имеем:

Из уравнений /3/, /4/ и /5/ имеем:

А 2 =M∙ (B+M+B) =M∙ (2B+M) = 2BM+M 2 /6/

Из уравнения /6/ имеем:

Отсюда: B = 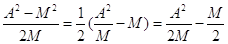/8/

Из уравнений /5/ и /8/ имеем:

C= 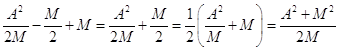/9/

B = 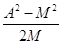/10/

C 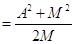/11/

Из уравнений /8/ и /9/ следует, что необходимым условием для того чтобы числа В и С были целыми, является делимость числа A 2 на число M, т.е. число M должно быть одним из множителей, входящих в состав множителей числа А или A 2 .

Числа А и M должны иметь одинаковую четность.

По формулам /10/ и /11/ определяются числа B и C как переменные, зависящие от значения числа А как параметра и значения числа M.

Из изложенного следует:

Квадрат простого числа A равен разности квадратов одной пары чисел B и C (при M=1).

Квадрат составного числа A равен разности квадратов одной пары или нескольких пар чисел B и C.

Все числа являются пифагоровыми.

Таким образом, существует бесконечное количество троек пифагоровых чисел А, В и С и, следовательно, бесконечное количество прямоугольных треугольников, у которых стороны А, В и С выражаются целыми числами.

Источник

Теорема Пифагора

О чем эта статья:

Основные понятия

Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Гипотенуза — сторона, лежащая напротив прямого угла.

Катет — одна из двух сторон, образующих прямой угол.

Формула Теоремы Пифагора выглядит так:

где a, b — катеты, с — гипотенуза.

Из этой формулы можно вывести следующее:

• a = √c 2 − b 2
• b = √c 2 − a 2
• c = √a 2 + b 2

Для фигуры со сторонами a, b и c, где c самая длинная сторона действуют следующие правила:

• если c 2 2 + b 2 , значит угол, обращенный к стороне c, является острым.
• если c 2 = a 2 + b 2 , значит угол, обращенный к стороне c, является прямым.
• если c 2 > a 2 +b 2 , значит угол, обращенный к стороне c, является тупым.

Записывайтесь на обучение по математике для учеников с 1 по 11 классы!

Теорема Пифагора: доказательство

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: ∆ABC, в котором ∠C = 90º.

Доказать: a 2 + b 2 = c 2 .

Пошаговое доказательство:

• Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
• Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:

• Также прямоугольная фигура ∆CBH подобна ∆ABC:

• Введем новые обозначения: BC = a, AC = b, AB = c.

• Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.

• Значит a 2 = c * HB, b 2 = c * AH.
• Сложим полученные равенства:

a 2 + b 2 = c * HB + c * AH

a 2 + b 2 = c * (HB + AH)

a 2 + b 2 = c * AB

Обратная теорема Пифагора: доказательство

Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такая фигура является прямоугольной.

Дано: ∆ABC

Доказать: ∠C = 90º

Пошаговое доказательство:

• Построим прямой угол с вершиной в точке C₁.
• Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.

• Проведём отрезок A₁B₁.
• Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.

• В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
• Таким образом получится:

• Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:

1. C₁A₁ = CA и C₁B₁ = CB по результату построения,
2. A₁B₁ = AB по доказанному результату.

• Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
• Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.

Обратная теорема доказана.

Решение задач

Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 10 см. Какое значение у гипотенузы?

значит c 2 = a 2 + b 2 = 6 2 + 10 2 = 36 + 100 = 136

Задание 2. Является ли фигура со сторонами 8 см, 9 см и 11 см прямоугольным треугольником?

• Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:

Ответ: треугольник не является прямоугольным.

Источник

О теореме Пифагора и способах ее доказательства

Статья опубликована при поддержке компании «Мастер перевода». Хотите качественный и быстрый перевод? Обратитесь в бюро нотариальных переводов «Мастер перевода». Качество услуг гарантировано постоянными клиентами бюро, среди которых множество именитых российских компаний. Посетите официальный сайт компании www.masterperevoda.ru и ознакомьтесь подробнее с предоставляемыми им услугами.

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

Это одна из самых известных геометрических теорем древности, называемая теоремой Пифагора. Ее и сейчас знают практически все, кто когда-либо изучал планиметрию. Мне кажется, что если мы хотим дать знать внеземным цивилизациям о существовании разумной жизни на Земле, то следует посылать в космос изображение Пифагоровой фигуры. Думаю, что если эту информацию смогут принять мыслящие существа, то они без сложной дешифровки сигнала поймут, что на Земле существует достаточно развитая цивилизация.

Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. С его именем связано много легенд. Достоверно известно, что Пифагор много путешествовал по странам Востока, посещал Египет и Вавилон. В одной из греческих колоний Южной Италии им была основана знаменитая «Пифагорова школа», сыгравшая важную роль в научной и политической жизни древней Греции. Именно Пифагору приписывают доказательство известной геометрической теоремы. На основе преданий, распространенных известными математиками (Прокл, Плутарх и др.), длительное время считали, что до Пифагора эта теорема не была известна, отсюда и название – теорема Пифагора.

Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т. е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий. Да и поныне сельские строители и плотники, закладывая фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы получить прямой угол. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении «Чжоу-би», написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам. Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Мы не знаем, как он это сделал. Некоторыми историками математики предполагается, что все же доказательство Пифагора было не принципиальным, а лишь подтверждением, проверкой этого свойства на ряде частных видов треугольников, начиная с равнобедренного прямоугольного треугольника, для которого оно очевидно следует из рис. 1.

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен, но стремление к преумножению их числа сохранилось. Думаю, что самостоятельное «открытие» доказательств теоремы Пифагора будет полезно и современным школьникам.

Рассмотрим некоторые примеры доказательств, которые могут подсказать направления таких поисков.

Доказательства, основанные на использовании понятия равновеликости фигур.

При этом можно рассмотреть доказательства, в которых квадрат, построенный на гипотенузе данного прямоугольного треугольника «складывается» из таких же фигур, что и квадраты, построенные на катетах. Можно рассматривать и такие доказательства, в которых применяется перестановка слагаемых фигур и учитывается ряд новых идей.

• На рис. 2 изображено два равных квадрата. Длина сторон каждого квадрата равна a + b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами a, b, то останутся равные площади, т. е. c 2 = a 2 + b 2 . Впрочем, древние индусы, которым принадлежит это рассуждение, обычно не записывали его, а сопровождали чертеж лишь одним словом: «смотри!» Вполне возможно, что такое же доказательство предложил и Пифагор.

Аддитивные доказательства.

Эти доказательства основаны на разложении квадратов, построенных на катетах, на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.

• Доказательство Энштейна (рис. 3) основано на разложении квадрата, построенного на гипотенузе, на 8 треугольников.

Здесь: ABC – прямоугольный треугольник с прямым углом C; C О MN; CK ^ MN; PO||MN; EF||MN.

Самостоятельно докажите попарное равенство треугольников, полученных при разбиении квадратов, построенных на катетах и гипотенузе.

• На рис. 4 приведено доказательство теоремы Пифагора с помощью разбиения ан-Найризия – средневекового багдадского комментатора «Начал» Евклида. В этом разбиении квадрат, построенный на гипотенузе, разбит на 3 треугольника и 2 четырехугольника. Здесь: ABC – прямоугольный треугольник с прямым углом C; DE = BF.

Докажите теорему с помощью этого разбиения.

• На основе доказательства ан-Найризия выполнено и другое разложение квадратов на попарно равные фигуры (рис. 5, здесь ABC – прямоугольный треугольник с прямым углом C).

• Еще одно доказательство методом разложения квадратов на равные части, называемое «колесом с лопастями», приведено на рис. 6. Здесь: ABC– прямоугольный треугольник с прямым углом C; O – центр квадрата, построенного на большом катете; пунктирные прямые, проходящие через точку O, перпендикулярны или параллельны гипотенузе.

• Это разложение квадратов интересно тем, что его попарно равные четырехугольники могут быть отображены друг на друга параллельным переносом. Может быть предложено много и других доказательств теоремы Пифагора с помощью разложения квадратов на фигуры.

Доказательства методом достроения.

Сущность этого метода состоит в том, что к квадратам, построенным на катетах, и к квадрату, построенному на гипотенузе, присоединяют равные фигуры таким образом, чтобы получились равновеликие фигуры.

• На рис. 7 изображена обычная Пифагорова фигура – прямоугольный треугольник ABC с построенными на его сторонах квадратами. К этой фигуре присоединены треугольники 1 и 2, равные исходному прямоугольному треугольнику.

Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь C О EP, прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ.

• На рис. 8 Пифагорова фигура достроена до прямоугольника, стороны которого параллельны соответствующим сторонам квадратов, построенных на катетах. Разобьем этот прямоугольник на треугольники и прямоугольники. Из полученного прямоугольника вначале отнимем все многоугольники 1, 2, 3, 4, 5, 6, 7, 8, 9, остался квадрат, построенный на гипотенузе. Затем из того же прямоугольника отнимем прямоугольники 5, 6, 7 и заштрихованные прямоугольники, получим квадраты, построенные на катетах.

Теперь докажем, что фигуры, вычитаемые в первом случае, равновелики фигурам, вычитаемым во втором случае.

• Рис. 9 иллюстрирует доказательство, приведенное Нассир-эд-Дином (1594 г.). Здесь: PCL – прямая;

KLOA = ACPF = ACED = a 2 ;

LGBO = CBMP = CBNQ = b 2 ;

AKGB = AKLO + LGBO = c 2 ;

отсюда c 2 = a 2 + b 2 .

• Рис. 10 иллюстрирует доказательство, приведенное Гофманом (1821 г.). Здесь Пифагорова фигура построена так, что квадраты лежат по одну сторону от прямой AB. Здесь:

OCLP = ACLF = ACED = b 2 ;

CBML = CBNQ = a 2 ;

OBMP = ABMF = c 2 ;

OBMP = OCLP + CBML;

c 2 = a 2 + b 2 .

• Рис. 11 иллюстрирует еще одно более оригинальное доказательство, предложенное Гофманом.
  Здесь: треугольник ABC с прямым углом C; отрезок BF перпендикулярен CB и равен ему, отрезок BE перпендикулярен AB и равен ему, отрезок AD перпендикулярен AC и равен ему; точки F, C, D принадлежат одной прямой; четырехугольники ADFB и ACBE равновелики, так как ABF=ECB; треугольники ADF и ACE равновелики; отнимем от обоих равновеликих четырехугольников общий для них треугольник ABC, получим

Алгебраический метод доказательства.

• Рис. 12 иллюстрирует доказательство великого индийского математика Бхаскари (знаменитого автора Лилавати, XII в.). Рисунок сопровождало лишь одно слово: СМОТРИ! Среди доказательств теоремы Пифагора алгебраическим методом первое место (возможно, самое древнее) занимает доказательство, использующее подобие.

• Приведем в современном изложении одно из таких доказательств, принадлежащих Пифагору.

На рис. 13 ABC – прямоугольный, C – прямой угол, CM ^ AB, b₁ – проекция катета b на гипотенузу, a₁ – проекция катета a на гипотенузу, h – высота треугольника, проведенная к гипотенузе.

Из того, что D ABC подобен D ACM следует

из того, что D ABC подобен D BCM следует

Складывая почленно равенства (1) и (2), получим a 2 + b 2 = cb₁ + ca₁ = c(b₁ + a₁) = c 2 .

Если Пифагор действительно предложил такое доказательство, то он был знаком и с целым рядом важных геометрических теорем, которые современные историки математики обычно приписывают Евклиду.

• Доказательство Мёльманна (рис. 14).
  Площадь данного прямоугольного треугольника, с одной стороны, равна с другой, где p – полупериметр треугольника, r – радиус вписанной в него окружности Имеем:

откуда следует, что c 2 =a 2 +b 2 .

• Доказательство Гарфилда.
  На рисунке 15 три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников. В первом случае эта площадь равна

во втором

Приравнивая эти выражения, получаем теорему Пифагора.

• Существует много доказательств теоремы Пифагора, проведенных как каждым из описанных методов, так и с помощью сочетания различных методов. Завершая обзор примеров различных доказательств, приведем еще рисунки, иллюстрирующие восемь способов, на которые имеются ссылки в «Началах» Евклида (рис. 16 – 23). На этих рисунках Пифагорова фигура изображена сплошной линией, а дополнительные построения – пунктирной.

Рекомендуем учителям предложить учащимся по этим рисункам самостоятельно доказать теорему Пифагора.

• Как уже было сказано выше, древние египтяне более 2000 лет тому назад практически пользовались свойствами треугольника со сторонами 3, 4, 5 для построения прямого угла, т. е. фактически применяли теорему, обратную теореме Пифагора. Приведем доказательство этой теоремы, основанное на признаке равенства треугольников (т. е. такое, которое можно очень рано ввести в школе). Итак, пусть стороны треугольника ABC (рис. 24) связаны соотношением

c 2 = a 2 + b 2 . (3)

• Докажем, что этот треугольник прямоугольный.
  Построим прямоугольный треугольник A₁B₁C₁ по двум катетам, длины которых равны длинам a и b катетов данного треугольника (рис. 25). Пусть длина гипотенузы построенного треугольника равна c₁. Так как построенный треугольник прямоугольный, то по теореме Пифагора имеем: c₁ 2 = a 2 + b 2 . (4)

Сравнивая соотношения (3) и (4), получаем, что

Таким образом, треугольники – данный и построенный – равны, так как имеют по три соответственно равные стороны. Угол C₁ прямой, поэтому и угол C данного треугольника тоже прямой.

• В заключение отметим, что о теореме Пифагора, ее истории и многих других связанных с ней геометрических фактах имеется обширная литература. Назову лишь некоторые источники:

1. Ван-дер-Варден Б.Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. М., 1959.
2. Глейзер Г.И. История математики в школе. М., 1982.
3. Еленьский Щ. По следам Пифагора. М., 1961.
4. Литцман В. Теорема Пифагора. М., 1960.
5. Скопец З.А. Геометрические миниатюры. М., 1990.

Источник