Алгебраические способы задания фигур

Алгебраические способы задания фигур

При решении геометрических задач обычно используются три основных метода: геометрический – когда требуемое утверждение выводится с помощью логических рассуждений из ряда известных теорем; алгебраический – когда искомая геометрическая величина вычисляется на основании различных зависимостей между элементами геометрических фигур непосредственно или с помощью уравнений; комбинированный – когда на одних этапах решение ведется геометрическим методом, а на других — алгебраическим.

Какой бы путь решения ни был выбран, успешность его использования зависит, естественно, от знания теорем и умения их применять.

Метод дополнительного построения

Всякое геометрическое решение геометрической задачи начинается с работы над чертежом. При этом иногда на «естественном» чертеже (т.е. на чертеже, на котором изображено только условие) трудно заметить связи между данными и искомыми величинами, а если фигуру достроить, эти связи становятся очевидными.

Две фигуры F и F ₁ называются подобными, если они переводятся друг в друга преобразованием подобия, т.е. таким преобразованием, при котором расстояния между точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз.

Признаки подобия треугольников:

1) Если два угла одного соответственно равны двум углам другого;

2) Если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами равны;

3) Если три стороны одного треугольника пропорциональны трем сторонам другого.

Метод замены широко применяется в алгебре, но не менее эффективно «замена» может быть применена в геометрии. Сущность этого приема решения геометрических задач состоит в следующем: фигура, о которой идет речь в условии задачи, так заменяется фигурой с той же искомой величиной, чтобы найти эту величину было легче.

Метод введения вспомогательного неизвестного

Суть метода заключается в том, что исходя из условия задачи составляют уравнение (или систему уравнений). В качестве вспомогательных аргументов удобно выбирать величины, которые вместе с данными из условия задачи дают набор элементов, однозначно задающих некоторую фигуру.

В математических задачах часто бывает полезен такой прием: двумя способами найти одну и ту же величину и приравнять полученные для нее выражения. Пусть мы, например, двумя способами нашли площадь некоторой фигуры. Если в одном из выражений для площади входит, скажем синус какого-либо угла α, то при помощи соотношения из полученного равенства можно получить некоторое неравенство, порой интересное.

Метод «вспомогательных объёмов»

Для нахождения расстояния от точки до плоскости или при нахождении углов между прямой и плоскостью метод «вспомогательного объёма» во многих случаях оказывается наиболее эффективным. Суть метода заключается в том, что объём некоторой фигуры выражается двумя способами, а затем из полученных равенств выражается искомая величина. Причём в этом методе нет необходимости строить проекцию прямой на плоскость или проекцию точки, что во многих случаях оказывается очень затруднительным.

Применение критериев коллинеарности и компланарности векторов в решении задач.

Критерии коллинеарности и компланарности векторов служат основной для применения векторной алгебры в решении стереометрических задач. Они позволяют выразить в виде векторных равенств различные утверждения о расположенных точках, прямых и плоскостей в пространстве. Переход от векторных равенств к скалярным происходит на основе единственности разложения вектора по двум неколлинеарным и трём некомпланарным векторам.

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. И, решая ту или иную геометрическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще, удобнее. Некоторые виды координатных систем, отличные от прямоугольных.

1.Косоугольные (аффинные) координаты.

Рассмотрим самые употребительные и простые координаты в пространстве, называемые прямоугольными. Их называют ещё декартовыми по имени Рене Декарта (1596-1650) – французского учёного и философа, впервые ввёдшего координаты в геометрию (на плоскость).

Источник

Геометрические задачи и методы их решения с примерами

Содержание:

Логическое построение геометрии

Геометрия — это наука о пространственной форме и количественных характеристиках предметов реального мира. Прочие свойства предметов изучают другие дисциплины. Если при изучении предмета учитывать только пространственную форму и размеры, то получим абстрактный объект, называемый геометрической фигурой.

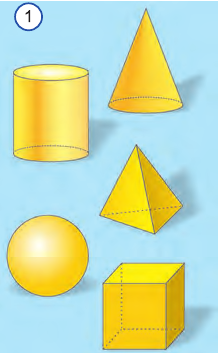
Слово «геометрия» — греческого происхождения и в переводе означает землеизмерение. Геометрию, изучаемую в школе, называют евклидовой по имени древнегреческого ученого Евклида. Геометрия состоит из двух частей: планиметрии и стереометрии. Планиметрия изучает свойства фигур на плоскости, а стереометрия — в пространстве (рис. 1).

Чтобы отличать геометрические фигуры друг от друга, их свойства описывают в виде утверждения, которое называют определением. Однако, определить вес геометрические фигуры невозможно. Некоторые из них, первоначальные, вынуждены принять без определения. Принимаем их за неопределяемые, начальные (основные) геометрические фигуры. Логическое построение геометрии осуществляют в следующем порядке: 1. Вначале принимают основные (начальные) геометрические фигуры без определения; 2. Принимают основные свойства этих фигур без доказательств;

3. Определяют другие геометрические фигуры через основные фигуры и их свойства, а затем доказывают свойства этих фигур и утверждений, истинность которых устанавливается путем доказательств, опираясь на известные.

Такое построение науки называют аксиоматическим построением. Свойства фигур, принятые без доказательства, называют аксиомами.

В планиметрии, которую мы изучали до сих пор основными геометрическими фигурами были точка и прямая. Их приняли без определения. Но определили отрезок, луч, треугольник и другие геометрические фигуры. Точно так же следующие свойства (утверждения) мы принимаем без доказательств в качестве аксиом:

I. Аксиомы принадлежности

1.1. Какова бы ни была прямая на плоскости, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

1.2. Через любые две точки можно провести прямую, и притом только одну.

II. Аксиомы расположения

2.1. Из трех точек, лежащих на прямой, одна и только одна лежит между двумя другими.

2.2. Любая прямая делит плоскость на две части: на две полуплоскости.

III. Аксиомы измерения

3.1. Любой отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

3.2. Любой угол имеет определенную градусную меру, большую нуля. Градусная мера развернутого угла равна 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

IV. Аксиомы откладывания

4.1. На любом луче от его начальной точки можно отложить единственный отрезок, равный данному.

4.2. От любого луча в определенную полуплоскость можно отложить единственный угол, равный данному, не развернутому углу.

4.3. Для любого треугольника существует единственный равный ему треугольник в заданном расположении относительно данного луча.

V. Аксиома параллельности

5.1. На плоскости через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Вывод некоторого утверждения с помощью логических размышлений называют доказательством. Утверждение, верность которого установлена с помощью доказательства, называют теоремой. Обычно теорема состоит из условия и заключения. В первой части теоремы — условии объясняют что задано. А во второй части — заключении формулируют что требуется доказать.

Доказать теорему — эго значит, используя ее условие, опираясь на принятые и доказанные ранее свойства, рассуждая, привести к правильности предложения, сформулированного в заключении.

Уточнение условия и заключения теоремы — разъясняет ее, облегчает понимание и доказательство теоремы.

Древнегреческий ученый Платон отмстил удивительную закономерность в геометрии: из свойств, изученных и доказанных ранее, логически размышляя и обдумывая, можно получить новые свойства. Следовательно, используя эти удивительные возможности, можно формулировать остальные свойства в виде теорем, которые доказывают с помощью логических размышлений, аксиом, а также свойств, доказанных до этого.

В процессе размышления запрещается использование недоказанных свойств, даже если их правильность очевидна.

Таким образом, если рассматривать геометрию как одно здание, начальные понятия и аксиомы составляют его фундамент. Кирпичи, уложенные на этом фундаменте — это новые определяемые понятия и свойства, доказанные в виде теорем.

В формировании геометрии в качестве самостоятельной науки большой вклад внесли древнегреческие ученые. Например, Гиппократ Хиосский дал разъяснения о первых геометрических понятиях. Наибольший вклад в этой области принадлежит великому древнегречеcкому ученому Евклиду (356-300 годы до нашей эры). Его основной труд «Начала» содержит планиметрию, стереометрию и некоторые вопросы теории вероятностей, кроме того, алгебру, основы теории отношений, способы вычисления площадей и объемов и также элементы теории пределов. Евклид в «Началах» собрал все достижения древнегреческих математиков того времени и создал основу для дальнейшего развития математики.

«Начала» состоят из 13 книг и содержат переработанные труды древнегреческих ученых V — IV веков до нашей эры. В нем приведены 23 определения, 5 постулатов и 9 аксиом. В этом труде даны правильные определения прямоугольника, квадрата и окружности. Для точки и прямой приведены следующие определения: «Точка-это то, что не имеет частей», «Линия-это длина без ширины».

В «Началах» приведены 9 аксиом — высказывания, принятые без доказательства. Также приведены следующие 5 математических умозаключений (постулатов), позволяющие осуществлять геометрические построения:

I. Через любые две точки можно провести только одну прямую.

II. Отрезок прямой можно бесконечно продолжить.

III. Из любой точки можно построить окружность произвольныго радиуса.

IV. Все прямые углы равны между собой.

V. Если две прямые, лежащие в одной плоскости, пересеченные третьей, образуют внутренние углы, сумма которых меньше двух прямых углов, то при продолжении вышеупомянутых прямых они пересекутся с той стороны, где сумма углов меньше двух прямых углов.

Упомянутый труд получил огромную славу и признание. Особенно V постулат стал причиной большой научной дискуссии. Если обозначить внутренние углы в V постулате а и (3 (рис. 1), а прямые а и b, то по смыслу этого постулата а+(3

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Геометрические методы решения алгебраических задач.
статья на тему

В статье рассказывается о методах решения алгебраических задач геометрическими методами.

Скачать:

Вложение	Размер
primenenie_geometrii_k_resheniyu_alg_zadach.docx	323.7 КБ

Предварительный просмотр:

Муниципальное автономное образовательное учреждение лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина

«Геометрические методы решения алгебраических задач»

Неверовская Светлана Владимировна

Учитель математики МАОУ лицей №14

ВВЕДЕНИЕ

Многие математические задачи допускают нескoлькo вaриaнтoв рeшeния. Нaхoждeниe нaибoлее прoстых путeй рeшeния нeрeдкo являются рeзультaтoм длитeльнoй и крoпoтливoй рaбoты. Часто первый избранный способ решения бывает крайне неудачным. Умение подбирать наиболее подходящее решение является одним из признаков хорошей математической подготовки. Существуют способы решения алгебраических задач методами, основанными на наглядно-геометрических интерпретациях.

Актуальность этой темы состоит в необходимости связи геометрии и алгебры, которые составляют единую науку математику. Также необходимо знать и уметь применять методы решения задач, которые помогут сэкономить время. Нередко различные олимпиады проверяют способность учеников применять различные нестандартные методы решения тех или иных задач. Для получения высоких баллов ЕГЭ необходимо уметь решать именно такие задания.

Объектом исследования является процесс решения алгебраических задач.

Предмет исследования – возможность применения геометрического метода в решении алгебраических задач.

Цель исследования – рассмотреть и овладеть различными геометрическими методами решения алгебраических задач.

В процессе работы я поставила перед собой следующие задачи :

• Показать, что преимуществом геометрического метода является наглядность;
• Классифицировать методы решения задач;
• Собрать методические материалы, включающие в себя задачи, решаемые различными методами.

ОСНОВНАЯ ЧАСТЬ

ПРИМЕНЕНИЕ ФОРМУЛ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Рассмотрим примеры задач, в которых удобно изобразить кривые или области в системе координат, которые соответствуют уравнениям или неизвестным, и рассмотреть их взаимное расположение:

• Уравнение окружности имеет вид , где и – координаты центра окружности .
• Уравнение прямой с угловым коэффициентом: , где – угловой коэффициент.
• Если прямая проходит через две точки и , такие что и то уравнение прямой можно найти, используя следующую формулу: .
• Расстояние между двумя точками на плоскости: , где – координаты одной точки, а – координаты другой точки.

Взаимное расположение окружностей:

• Одна окружность лежит внутри другой: расстояние между центрами окружностей меньше их радиусов( ).
• Одна окружностей касается другой изнутри: расстояние между центрами окружностей равно разности их радиусов( ).
• Окружности пересекаются: расстояние между центрами окружностей больше разности их радиусов, но меньше суммы( ).
• Одна окружность касается другой снаружи: Расстояние между центрами окружностей равно сумме их радиусов( ).
• Одна окружность лежит вне другой: расстояние между центрами окружностей больше суммы их радиусов( ).

Взаимное расположение окружности и прямой:

• Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки (пересекаются в двух точках).
• Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку (касаются). В этом случае прямая называется касательной к окружности. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
• Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек (не пересекаются).

Пример 1 (Химический факультет МГУ, 1996 г.):

После замены система имеет вид:

Так как переменные и связаны друг с другом с помощью величины , они не меняются независимо. Тогда, будем считать, что и – независимые переменные, и изобразим на координатной плоскости геометрическое место точек , координаты которых удовлетворяют системе:

Заштрихованное на рисунке 1 множество точек соответствует неравенству .

Заштрихованное на рисунке 2 множество точек соответствует неравенству .

Множество точек, удовлетворяющих системе (!) – это пересечение множеств заштрихованных на рисунке 1 и на рисунке 2 и первого координатного угла. Найдем это множество:

Понятно, что пересечение множеств — точка K(1,1).

Система (!) имеет единственное решение

Пример 2 (Географический факультет МГУ, 1994 г.):

Найти все значения параметра , при каждом из которых уравнение

имеет ровно одно решение.

Преобразуем уравнение следующим образом:

Изобразим на координатной плоскости OXY графики функций и , далее мы должны будем отобрать все значения , при которых эти графики пересекаются только в одной точке.

Равенство равносильно системе:

Геометрически системе (1) соответствует нижняя полуокружность , которая отделяется от окружности с центром радиуса 1 прямой .

Аналогично, равенству соответствует нижняя полуокружность ,которая отделяется от окружности с центром радиуса 1 прямой .

Изобразим эти полуокружности на рисунке 4:

С изменением параметра , центр перемещается по прямой . При перемещении центра подвижной окружности , мы видим, что

• при и полуокружности вообще не пересекаются,
• при и полуокружности пересекаются ровно в одной точке,
• при они совпадают.

На рисунке 5 изображены два крайних случая: , который соответствует , и , который соотвествует .

Найти все значения, которые может принимать функция при условии

Отобразив все это неравенства в системе координат, мы получили треугольник с вершинами Рассмотрим функцию , которая является квадратом расстояния от некоторой точки, которая находится где-то на этом треугольнике, до начала координат. Наименьшее значение наша функция принимает на прямой . Функция принимает наибольшее значение при (точка, которая соответствует нашему условию, — основание перпендикуляра, который был опущен из , а значение – это квадрат длины перпендикуляра). Отсюда мы получаем, что наибольшее значение, а именно – 17, функция принимает в точке .

Найти все значения параметра , при которых система

имеет хотя бы одно решение.

Стоит заметить, что в (1) неравенстве нам даны либо в квадрате, либо по модулю. Тогда можно сделать следующий вывод: если — решение неравенства, то и также являются решениями неравенства. Итак, множество точек, которые удовлетворяют этому неравенству, симметрично относительно обеих осей координат.

Рассмотрим случай, когда . Тогда проведем преобразования и получим следующее: . Мы получили круг единичного радиуса с центром в точке (3;3). Конечное множество точек изображено на рисунке.

Равенство (2) можно переписать в следующем виде: . Оно является уравнением окружности с центром в точке и радиусом .

Расстояние от точки до точек ближнего к ней круга (например, возьмем круг, находящийся в первой четверти) принимает значения из промежутка , а расстояние от точки до точек дальнего от нее круга изменятся в пределах .

Тогда у системы существуют решения только тогда, когда (1) и (2) имеют пересечение друг с другом. Таким образом, так как , необходимым и достаточным условием является требование .

Прежде чем приступать к решению, вспомним кое-что из теории. Вспомним, чему равно расстояние между двумя точками и .

1. Рассмотрим первое уравнение. Возьмем точки и . Тогда – искомая. Найдем расстояния между этими точками: , , .

По первому уравнению мы видим, что . Пусть эти точки не лежат на одной прямой, тогда они образуют треугольник. А это значит, что мы можем использовать неравенство треугольника, т.е. . Получается, что единственный возможный вариант – , а это значит, что точки лежат на одной прямой( . Используем уравнение прямой , подставив численные значения, получим следующее: .

1. Рассмотрим второе уравнение. Возьмем точки и D(6;4), точка – по-прежнему искомая. Найдем расстояния между точками: , , . Аналогично ( . Используем уравнение прямой и получим . Используем то, что мы получили из первого уравнения. .

ИСПОЛЬЗОВАНИЕ ТЕОРЕМ ГЕОМЕТРИИ

Рассмотрим примеры задач, в которых можно истолковать уравнение или неравенство как алгебраическое соотношение между длинами сторон и углами в каких-либо геометрических фигурах (треугольник, параллелограмм и т. п.), пользуясь теоремами геометрии ( теорема синусов, теорема косинусов и т.п.).

• Теорема синусов: .
• Теорема косинусов: .
• Теорема Пифагора: .

Найти наименьшее значение выражения , если .

Это выражение можно интерпретировать как сумму гипотенуз прямоугольных треугольников с катетами 1 и , 2 и , 3 и соответственно. По условию сумма длин катетов равна 8. Однако в геометрической интерпретации данные в условии задачи числа рассматриваются как длины отрезков, а длина всегда является числом положительным, а в задаче числа могут быть как положительными, так и отрицательными. Именно поэтому возникают различные варианты :

• Числа — одного знака, то есть либо все положительные, либо все отрицательные (см. рисунок 6а).
• Два любых числа (пусть будут одного знака, а третье – другого. В геометрической интерпретации будут браться модули этих чисел (см. рисунок 6б).

Решения для этих случаев будут отличаться всего лишь чертежом.

В чертеже эти треугольники удобнее расположить так, чтобы их катеты были соответственно параллельны. Тогда получается, что , , .

Соединим точки и . Длина отрезка, соединяющего концы ломанной, не может превышать длину самой ломанной. Отсюда получаем, что . Равенство будет достигаться при условии, что . Мы получим треугольник с прямыми углом и катетами , тогда гипотенуза . И следовательно и наименьшее значение – 10.

Дана система уравнений , и .

1. Преобразуем первое уравнение:

Мы получили теорему косинусов для треугольника со сторонами .

1. Преобразуем второе уравнение:

Мы получили теорему Пифагора для прямоугольного треугольника со сторонами

1. Преобразуем третье уравнение:

Мы получили теорему косинусов для треугольника с углом в и со сторонами

Собрав полученное во едино, мы получили рисунок 8:

Мы получили прямоугольный треугольник, площадь которого равна .

Однако площадь данного треугольника можно найти, просуммировав площади малых треугольников. . Отсюда следует, что искомое выражение .

Рассмотрим прямоугольный треугольник с катетами .

Далее разделим прямой угол на три равные между собой части и отложим на полученный лучах отрезки (рассматриваем случай, когда эти величины положительны, а иначе их нужно отложить в противоположную сторону).

Используя теорему косинусов, получим, что слагаемые, которые располагаются в левой части, соответственно равны . Тогда мы имеем .Из этого следует, что точки находятся на гипотенузе , при этом – биссектриса треугольника , а — биссектриса треугольника . Использовуя формулу биссектрисы, мы получим следующее: .

Преобразовав систему, находим .

ПРИМЕНЕНИЕ ПОНЯТИЯ ВЕКТОРА

Использование понятия вектора для решения алгебраических задач.

• Вектор в трехмерном пространстве характеризуется тремя координатами и его модуль (длина) вычисляется по формуле .
• При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число , т.е. и .
• Два отличных от нуля вектора называют коллинеарными, если они лежат на одной прямой или на параллельных прямых. У коллинеарных векторов соответствующие координаты пропорциональны.
• Для векторов и справедливо неравенство . Эту формулу называют неравенством треугольника. Заметим, что равенство достигается, когда векторы коллинеарные.
• Скалярным произведением векторов и называют число , где — угол между векторами . В координатной форме .

Рассмотрим примеры задач, в решении которых удобно применить векторный подход.

Применение векторов для доказательства неравенств

Доказать, что если , то .

Рассмотрим на плоскости векторы:

Если в последнее неравенство подставить выражения для длин векторов , то получим неравенство, которое требуется доказать.

Для доказать неравенство: .

Рассмотрим в пространстве векторы: , , и так как , то

Так как , то подставив в это неравенство ранее полученные выражения получим:

и возведя обе части в квадрат, получим неравенство, которое необходимо доказать.

Применение векторов для решения уравнений

Рассмотрим на плоскости векторы: тогда и . Подставив полученные выражения в исходное уравнение, получим , что говорит о том, что векторы коллинеарные и имеет место равенство .

Уравнение определено для . Возведя обе части в квадрат, получим уравнение , которое имеет корни . Учитывая, что . Получаем корни уравнения .

Рассмотрим в пространстве векторы: , тогда и . Пусть , тогда и .

В таком случае исходное уравнение принимает вид: . Следовательно, что векторы коллинеарные и имеет место равенство . Отсюда получаем систему уравнений или

Решениями системы являются .

Применение векторов к решению неравенств

Рассмотрим на плоскости векторы: .

Тогда . Пусть , тогда , .

Поскольку , то имеет место неравенство треугольника: или .

Если в это неравенство подставить ранее полученные выражения, то получим: и сравнивая с данным неравенством, получим, , что будет означать и что векторы коллинеарные и имеет место равенство .Откуда .

Областью допустимых значений переменной в неравенстве являются .

Рассмотрим в трехмерном пространстве два вектора

Так как , и , то исходное неравенство принимает вид: . что является тождеством, и мы делаем вывод, что исходное неравенство верно для всех допустимых х из области определения.

Следовательно, решением неравенства являются .

Применение векторов к решению систем

Решить систему уравнений: .

Рассмотрим на плоскости векторы: ,

Пусть , тогда , , . Тогда первое уравнение системы принимает вид , а это означает, что векторы коллинеарные и имеет место равенство .Если , то уравнение не имеет решений.

Пусть . Подставив в исходную систему, получим: . Откуда .

Поскольку , то векторы противоположно направлены, следовательно, для должно выполняться неравенство (выполняется).

Решить систему уравнений: .

Рассмотрим на плоскости векторы:

Пусть . Тогда из исходной системы следует, что и тогда .

Так как , то . Имеем , то есть неравенство превращается в равенство. А это означает, что векторы являются коллинеарными, а значит, имеет место равенство .

Решениями полученного равенства являются .

Среди всех решений системы найти такие, при каждом из которых выражение принимает наибольшее значение.

Рассмотрим на плоскости векторы: если координаты этих векторов удовлетворяют всем условиям системы, то из первого уравнения следует, что .

Левая часть последнего неравенства системы это скалярное произведение в координатах, тогда .

С другой стороны . Учитывая оба условия, получаем, что , значит, и векторы сонаправлены, то есть , где . Число .Значит, .

Выражение принимает вид: , где .

Так как , где — угол между векторами , то наибольшее значение выражение достигается, если и векторы сонаправлены, то есть , где . Число .

Итак, выражение принимает наибольшее значение при .

Применение векторов к нахождению наибольших и наименьших значений

Найти наибольшее значение выражения .

Рассмотрим на плоскости векторы: , тогда .

Имеем , где — угол между векторами . Так как , то . Если положить ( при этом векторы становятся сонаправленными), то .

Найти наименьшее значение функции .

Перепишем функцию в виде

Рассмотрим на плоскости векторы: тогда и .

Поскольку , то и .

Теперь необходимо показать, что существуют значения переменных при которых .

Если , то , то есть и векторы коллинеарные и или . Пусть , тогда и . Следовательно, наименьшее значение функции равно .

Ответ: наименьшее значение функции равно .

ПРИМЕНЕНИЕ ГЕОМЕТРИИ К РЕШЕНИЮ ЗАДАЧ ТРИГОНОМЕТРИИ

Применение геометрии в тригонометрии.

• Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
• Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
• Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Использования геометрического метода порой упрощает задания до неузнаваемости.

Преобразуем данное выражение.

( ), ( Так как . Получим, что и значение выражения равно .

Найти значение выражения:

Пусть . Построим прямоугольный треугольник со сторонами . Тогда по теореме Пифагора . Из этого треугольника найдем . Тогда значение выражения .

Рассмотрим равнобедренный треугольник с углом при вершине и высотой ВВ 1 =1. Из треугольников ABB 1 , BDB 1 , BCB 1 мы находим AB=AC= , BD=AD= , BC= . Заметим, что AC=AD+CD. Откуда мы и получим данное неравенство.

В этой работе я показала, что практически в каждом разделе алгебры существуют задания, геометрическое решение которых намного рациональнее, чем традиционное. Мне удалось достичь цели моего исследования: я овладела способами решения алгебраических задач геометрическими методами и теперь смогу применять полученные знания на экзаменах и олимпиадах. Я рассмотрела много алгебраических заданий, решаемых с помощью геометрии, классифицировала их. Изучила геометрические способы решения систем, задач, содержащих иррациональность. Применила геометрический метод решения к тригонометрическим заданиям. Познакомилась с векторным методом решения уравнений и доказательства неравенств.

В результате проделанной работы я пришла к следующим выводам:

• При решении некоторых задач геометрическими методами наблюдается явно выраженная экономия сил, энергии, а главное времени;
• Чертеж помогает расширить задачу – поставить и решить общие вопросы, глубже проникнуть в существо задачи, оценить реальность результата и промежуточных действий;
• Чтобы решить алгебраическую задачу геометрическим методом необходимо иметь навык и «видение» геометрической интерпретации задачи, что, на мой взгляд, и является самым сложным в данном методе;
• Во многих разделах алгебры существуют классы задач, решаемых геометрическими методами;
• Чтобы решить задачу геометрическими методами необходимо иметь мощную базу знаний по геометрии, т.к. в решении используются: метод площадей, векторная геометрия, свойства геометрических фигур, геометрические неравенства и т.п.

Работая с различными сборниками задач и статьями в математических журналах, считаю нужным отметить отрывочность рассмотрения этой темы. Негеометрические задачи, решаемые геометрическими методами, встречаются в них или в разделе нестандартных методов решения задач, где приводится решение одного — двух примеров или вообще не выделяются в отдельный класс. Именно этим объясняется достаточно большой список информационных источников. Во многих сборниках задания приводились лишь с указаниями к решению и ответом, поэтому мне приходилось самостоятельно доводить решение до логического конца. Но именно эта работа позволила более глубоко понять предложенный метод решения.

Источник