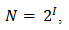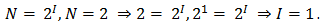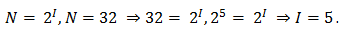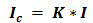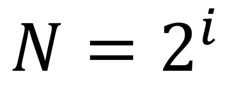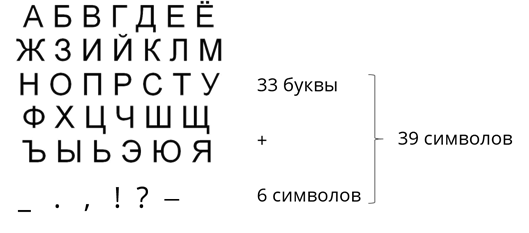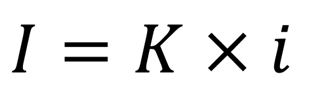Алфавитный способ измерения информации информатика

Алфавитный подход к определению количества информации

Цели урока:

1) Обучающая: рассмотреть алфавитный подход к измерению количества информации, научиться вычислять количество информации с точки зрения алфавитного подхода.

2) Развивающая: развитие у учащихся самостоятельности и познавательной активности.

3) Воспитывающая: воспитывать дисциплинированность, аккуратность, собранность.

Литература:

1) Угринович Н. Д. «Информатика 8 класс»,

2) Заславская О. Ю., Левченко И. В. «Информатика: весь курс».

1) Угринович Н. Д. «Информатика 8 класс».

Тип урока: ознакомление с новым материалом

План урока:

1. Организационный этап.

2. Актуализация знаний.

3. Подготовка учащихся к усвоению нового материала.

4. Этап получения новых знаний.

5. Этап обобщения и закрепления нового материала.

7. Заключительный этап.

Ход урока

1. Организационный этап.

Здравствуйте. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

1) В чём заключается содержательный подход к измерению информации? (Количество информации — мера уменьшения неопределённости знаний при получении информационных сообщений.)

2) Какую минимальную единицу информации используют для измерения количества информации? (Бит)

3) Какую формулу используют для определения количества информации? (Формулу Хартли)

4) Производится бросание симметричной четырехгранной пирамидки. Какое количество информации мы получаем в зрительном сообщении о ее падении на одну из граней? (2 бита)

6) Из непрозрачного мешочка вынимают шарики с номерами и известно, что информационное сообщение о номере шарика несет 5 битов информации. Определите количество шариков в мешочке. (35)

3. Этап получения новых знаний.

Скачать видеоурок «Алфавитный подход к определению количества информации»

Содержательный подход к измерению информации рассматривает информацию с точки зрения человека, как уменьшение неопределенности наших знаний.

Однако любое техническое устройство не воспринимает содержание информации. Поэтому в вычислительной технике используется другой подход к определению количества информации. Он называется алфавитным подходом.

При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.

Проще всего разобраться в этом на примере текста, написанного на каком-нибудь языке. Для нас удобнее, чтобы это был русский язык.

Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, пропуск между словами.

Алфавит — это множество символов, используемых при записи текста.

Мощность (размер) алфавита — это полное количество символов в алфавите.

Мощность алфавита обозначается буквой N.

· мощность алфавита из русских букв равна 33;

· мощность алфавита из латинских букв — 26;

· мощность алфавита текста набранного с клавиатуры равна 256 (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания );

· мощность двоичного алфавита равна 2.

При алфавитном подходе считается, что каждый символ текста имеет информационную емкость. Информационная емкость знака зависит от мощности алфавита.

Алфавит, с помощью которого записано сообщение состоит из N знаков. В простейшем случае, когда длина кода сообщения составляет один знак, отправитель может послать одно из N возможных сообщений, которое будет нести количество информации I.

Тогда в формуле

N — количество знаков в алфавите знаковой системы, I — количество информации, которое несет каждый знак.

Например, из формулы можно определить количество информации, которое несет знак в двоичной знаковой системе

Информационная емкость знака двоичной знаковой системы составляет 1 бит.

Задача 1. Определите, какое количество информации несет буква русского алфавита (без буквы ё).

Буква русского алфавита несет 5 битов информации.

Формула 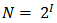связывает между собой количество возможных событий и количество информации, которое несёт полученное сообщение. В рассматриваемой ситуации N — это количество знаков в алфавите, знаковой системы, а I — количество информации, которое несёт один знак.

Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.

Количество информации в сообщении можно посчитать, умножив количество информации, которое несет один знак на количество знаков в сообщении.

где 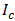— количество информации в сообщении

— количество информации, которое несет один знак

— количество знаков в сообщении

Давайте решим с вами задачу.

Задача 2. Какое количество информации содержит слово «ПРИВЕТ», если считать, что алфавит состоит из 32 букв?

Решение. Что нам требуется найти в данной задаче? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».

Что нам для этого дано?

Дано: количество знаков в сообщение и мощность алфавита.

Количество знаков в сообщении равно 6, а мощность данного алфавита равна 32.

Что нам нужно найти? Нам нужно найти какое количество информации содержит слово «ПРИВЕТ».

Посмотрим на наше сообщение, оно содержит несколько знаков, значит для того чтобы найти количество информации нашего сообщения, нам нужно умножив количество информации, которое несет один знак, на количество знаков в сообщении, воспользоваться формулой «и» суммарное равно «и» умножить на «к».

Но мы еще не можем воспользоваться формулой, т.к. не знаем какое количество информации несет один знак. Для этого воспользуемся формулой Хартли. Сообщение записано с помощью алфавита, мощность которого равна 32, N равно 32. Мы получили уравнение. Решив это уравнение, мы получили, что количество информации, которое несет один знак нашего алфавита, равно 5 бит. Зная количество информации, которое несет один знак нашего алфавита, и количество знаков в сообщении, мы можем найти какое количество информации содержит наше сообщение.

Итак, наше сообщение содержит 30 бит.

4. Этап обобщения и закрепления нового материала.

1) Какое количество информации содержит слово «ИНФОРМАТИКА», если считать, что алфавит состоит из 32 букв? (55 битов)

2) Определить количество информации, содержащееся в слове из 10 символов, если известно, что мощность алфавита равна 32 символам. (50 бит)

3) Сколько бит информации содержится в сообщении, состоящем из 5 символов, при использовании алфавита, состоящего из 64 символов. (6 битов)

4) Определить информативность сообщения «А + В = С», если для описания математических формул необходимо воспользоваться 64-символьным алфавитом. (30 бит)

5) Для представления числовых данных используют 16-ричный алфавит, включающий знаки математических действий. Сколько битов информации содержит выражение «32 * 5 = 160»? (32 бита)

6) Практическая работа № 2. «Тренировка ввода текстовой и числовой информации с помощью клавиатурного тренажера»

5. Рефлексия.

Источник

Алфавитный способ измерения информации информатика

Измерение информации: содержательный и алфавитный подходы. Единицы измерения информации.

Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.

Содержательный подход к измерению информации.
Для человека информация — это знания человека. Рассмотрим вопрос с этой точки зрения.
Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно.
Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2×2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника.
Но для того чтобы сообщение было информативно оно должно еще быть понятно. Быть понятным, значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей.
Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека.
Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными.

Алфавитный подход к измерению информации.

А теперь познакомимся с другим способом измерения информации. Этот способ не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.
Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54.
При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.
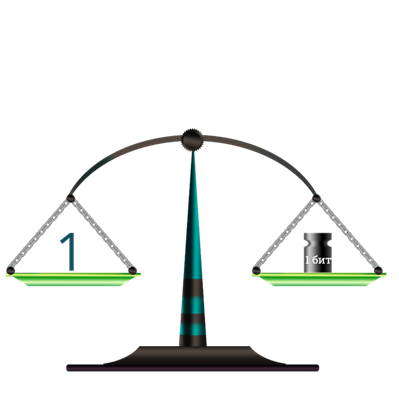
При использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации. Интересно, что сама единица измерения информации «бит» получила свое название от английского сочетания «binary digit» — «двоичная цифра».

1 бит — это минимальная единица измерения информации!

Один символ алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт.

Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.

В любой системе единиц измерения существуют основные единицы и производные от них.

Для измерения больших объемов информации используются следующие производные от байта единицы:

Источник

Измерение информации. Алфавитный подход

Урок 4. Информатика 10 класс (ФГОС)

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Измерение информации. Алфавитный подход»

· алфавитный (объёмный) подход к измерению информации;

· связь между алфавитным подходом к измерению информации и содержанием информации;

· единицы измерения объёма письменного или печатного текста.

Процесс познания окружающего мира приводит к накоплению информации в форме знаний. Как же узнать, много получено информации или нет?

Из прошлых уроков вы знаете, что информацию можно собирать, обрабатывать, хранить, и передавать.

Но тогда очень важно понимать хватит ли места на носителе, чтобы сохранить нужную информацию. Или сколько времени нужно, чтобы передать информацию по каналу связи.

Как вы понимаете, нам просто необходимо научиться измерять информацию.

В компьютерных (цифровых) системах хранения и передачи информации применяется алфавитный подход к измерению информации. Здесь используется двоичный способ кодирования информации и важен только размер или объём хранимого и передаваемого кода. Именно поэтому алфавитный подход также называют объёмным.

Мы уже говорили о том, что разрядность двоичного кода i и количество возможных кодовых комбинаций или мощность алфавита N связаны соотношением:

Рассмотрим систему кодирования английского алфавита.

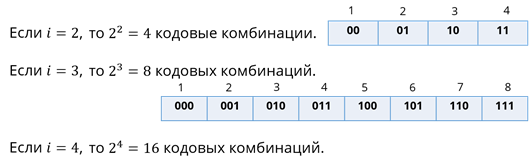
Английский алфавит состоит из 26 букв. Добавляем сюда же пробел, точку, запятую, вопросительный и восклицательный знаки, тире, то есть ещё 6 символов. Тогда расширенный алфавит состоит из 32 символов.

Так как 32 = 2 5 значит, все символы можно закодировать пятиразрядными двоичными кодами от пяти нулей до пяти единиц.

Мы уже встречали такой пятиразрядный код, когда изучали телеграфные аппараты, появившиеся в девятнадцатом веке. Помните код Бодо?

В двоичном коде каждая двоичная цифра несёт одну единицу информации, которую называют один бит. Именно бит является единицей измерения информации.

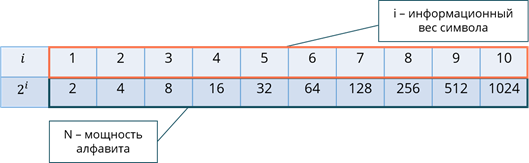
Длина двоичного кода, с помощью которого кодируется символ алфавита, называется информационным весом символа. Так, например, информационный вес символа расширенного английского алфавита равен пяти битам.

Информационный объем текста складывается из информационных весов всех символов, составляющих текст. Например, английский текст из тысячи символов в телеграфном сообщении будет иметь информационный объем пять тысяч бит.

Теперь рассмотрим систему кодирования русского языка. Русский алфавит состоит из 33 букв. Добавляем к нему те же 6 дополнительных символов, что и для английского алфавита, получаем набор из 39 символов.

Понятно, что пятиразрядного кода нам уже не хватает. Попробуем шестиразрядный код.

Так как 2 6 = 64, остаются свободные 25 символов, которые можно, использовать, например, для кодирования цифр, скобок и знаков математических операций.

Соответственно, информационный вес символа в расширенном русском алфавите будет равен 6 бит. А текст, состоящий из 1000 символов будет иметь объем 6000 бит.

Данное следствие можно записать в виде формулы:

информационный объём сообщения I равен произведению количества символов К в сообщении умноженному на информационный вес символа алфавита i.

Измерять количество информации через длину двоичного кода придумал выдающийся российский математик Андрей Николаевич Колмогоров. Он решил, что количество информации, содержащийся в тексте, определяется минимально возможной длиной двоичного кода, необходимого для представления этого текста.

Зная ряд целых степеней двойки можно быстро определить информационный вес символа.

Если N – это мощность алфавита, оказывается не целой степенью двойки, тогда находят ближайшее к N значение во второй строке таблицы, но большее чем N. Причём значение i в первой строке будет равно информационному весу символа.

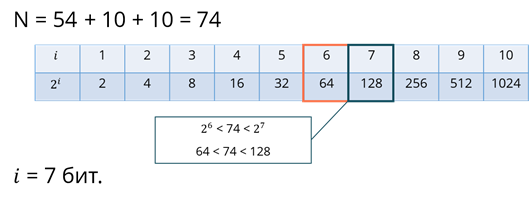
Рассмотрим пример. Необходимо определить информационный вес символа испанского алфавита, включающего в себя 54 строчные и прописные буквы; 10 цифр; 10 знаков препинания, скобок, кавычек.

Итак, сначала узнаем общее количество всех символов. Для этого нужно сложить все символы.

Теперь посмотрим на таблицу степеней двойки.

Это означает, что все 74 символа можно закодировать семиразрядными двоичными кодами.

В современных компьютерах чаще всего применяется восьмиразрядный код для двоичного представления текстов. Восьмиразрядный двоичный код позволяет получить 256 различных кодовых комбинаций, то есть 2 8 = 256.

Такой код содержится, например, в операционной системе Windows в кодовой таблице ANSI. Он включает в себя английские и русские буквы – прописные и строчные, цифры, знаки препинания, знаки арифметических операций, скобки и другое.

Для измерения информационного объёма памяти компьютера используются байты. Причём, 1 байт = 8 бит.

Рассмотрим пример. Пользователь компьютера, хорошо владеющий навыками ввода информации с клавиатуры, может вводить в минуту 100 знаков. Мощность алфавита, используемого в компьютере равна 256 символов. Нужно определить какое количество информации в байтах может ввести пользователь в компьютер за одну минуту.

Также для измерения информации используются кратные единицы.

Вся информация в компьютере представляется в виде двоичного кода. Это и тексты, и звуки, рисунки, видео и многое другое.

Объем информации любого вида, выраженный в битах равен длине двоичного кода, в котором эта информация представлена.

Рассмотрим пример. Учебник содержит 160 страниц. На каждой странице — 60 строк. В каждой строке 70 символов (включая пробелы). Нужно найти информационный объем текста, если используется восьмиразрядная кодировка.

В компьютерных (цифровых) системах хранения и передачи информации применяется алфавитный подход измерения информации. Здесь используется двоичный способ кодирования информации и важен только размер или объём хранимого и передаваемого кода. Именно поэтому алфавитный подход также называют объёмным.

Информационный объем текста складывается из информационных весов всех символов, составляющих текст.

Объем информации равен длине двоичного кода

Основная единица: 1 бит — один разряд двоичного кода. А также применяются производные единицы: байт, Кб, Мб, Гб и Тб.

Источник