Построение аксонометрических проекций окружности
Построение аксонометрических проекций окружности вызывает трудности, в связи с тем, что окружность принимает вид эллипса в аксонометрии. Возникает вопрос: как рисовать эллипс? Чтобы построить окружность в аксонометрии используют следующие способы: — построение по вспомогательной квадратной сетке; — построение при помощи циркуля;
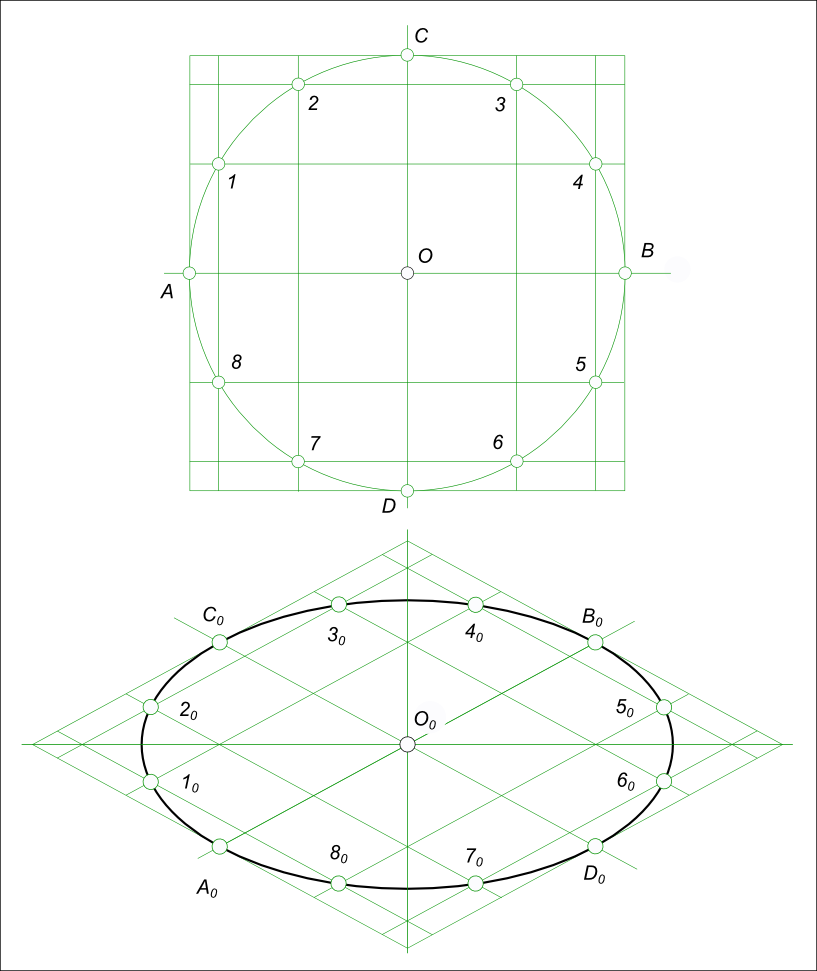
По первому способу квадрат описывает окружность и делится на 4×4=16. Отмечаем точки пересечения линий сетки с линией окружности. Затем строим аксонометрическую проекцию сетки и на ней отмечаем точки A0, 10, 20, . 80. По этим точкам строим окружность, при помощи лекала. Данным способом окружность строится также в перспективе.
Окружность для данного вида аксонометрической проекции — прямоугольной изометрии получилась получилась несколько больше своего действительного размера, в следствии применения приведенных коэффициентов искажения.
По второму способу окружность строится при помощи циркуля Построение аксонометрических проекций окружности в косоугольной фронтальной диметрии
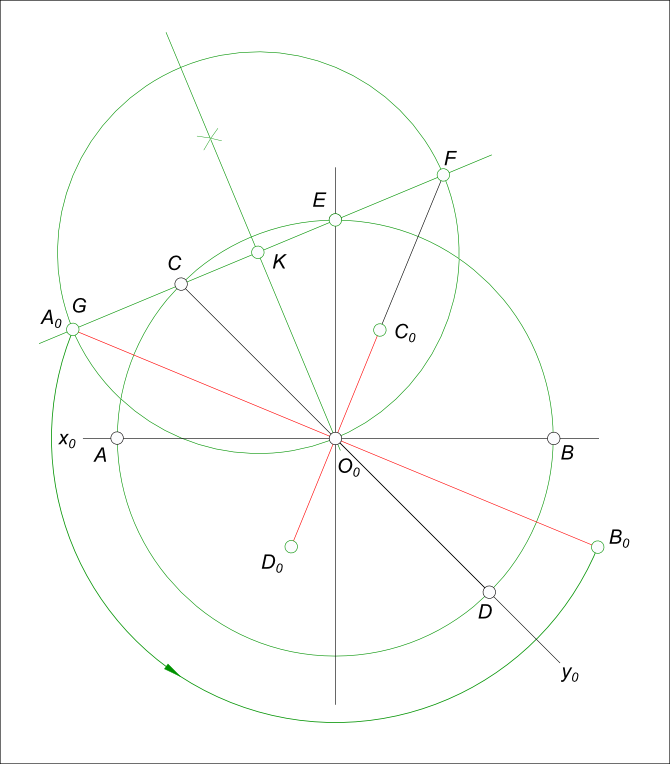
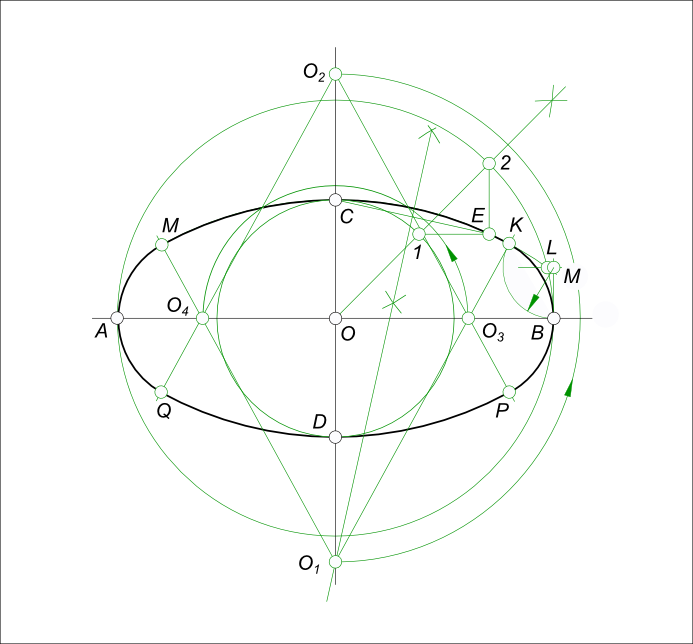
Пусть окружность расположена параллельно горизонтальной плоскости проекции: — сначала определяем направление большой и малой оси эллипса, используя для этого построение показанное на рисунке Сопрягаемые диаметры AB и CD построены на аксонометрических осях x0 и y0, их центры совпадают с началом координат. Концы одного из диаметров (AB) соединим дугой окружности из центра O0. Восстановив перпендикуляр к диаметру в точке O0 отметим на их пересечении точку E. Соединяем точки C, E прямой линией. Находим середину отрезка CE — точку K. Из точки K описываем окружность радиусом KO0 и отмечаем точки F и G, в которых она пересекается с прямой CE. Длина половины большой оси равна отрезкам GE, CF, длина половины малой оси равна отрезкам CG, EF; — затем, после построения осей эллипса:
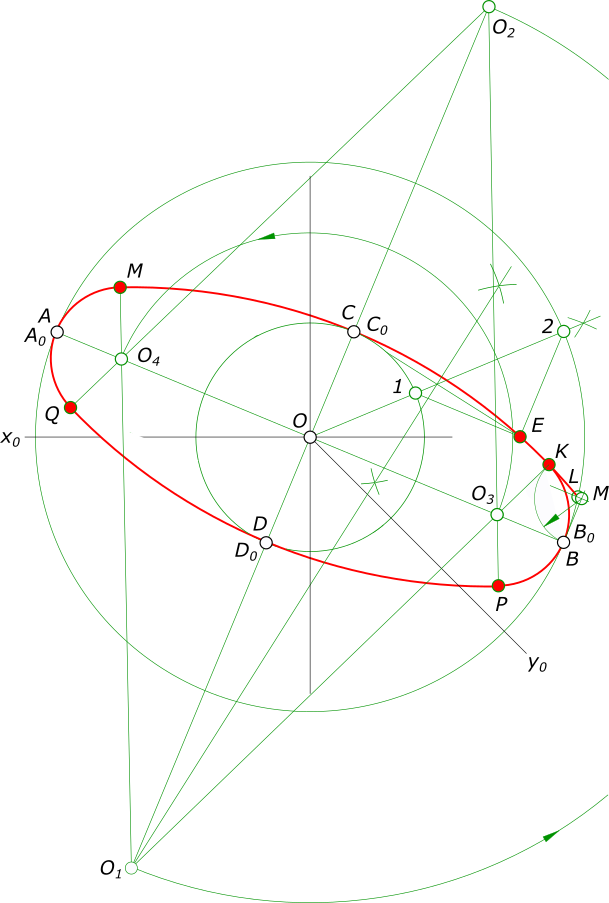
— проводим прямую O — 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; — из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; — соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O1, которая определяет центр дуги CE; — строим точку O2 симметричную O1, относительно центра эллипса — O; — на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси — OB; — из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; — соединив прямой линией точки K и O1 на пересечении ее с большой осью находим точку O3, являющуюся центром дуги BK; — точку P находим на пересечении прямой O2O3 с дугой радиусом O3B. P — точка сопряжения дуг BK и BP; — точке O3 симметрична относительно центра эллипса точка O4; — аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения.
Построение аксонометрических проекций окружности в прямоугольной изометрии
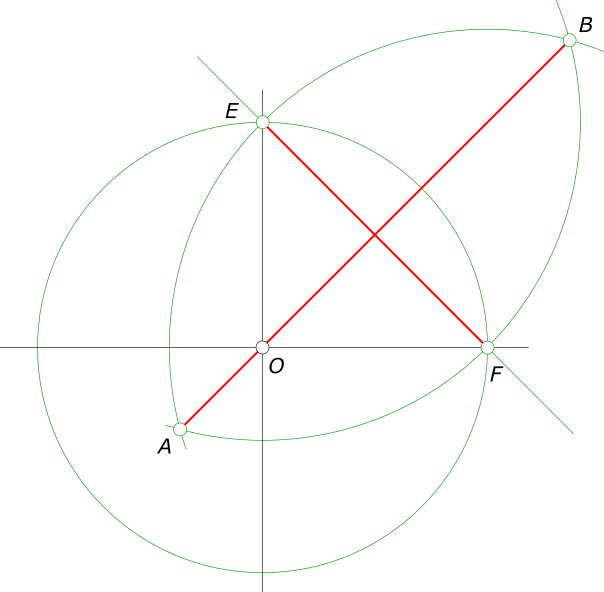
Графически определяем размеры осей эллипса: — проводим две взаимно перпендикулярные линии; — приняв точку их пересечения за центр O, описываем из него окружность заданного диаметра и отмечаем точки E и F; — из точек E и F описываем дуги радиусом R = EF = FE и находим точки их пересечения A и B; — соединив точки A и B, получим большую ось эллипса, равную 1,22d; — соединив точки E и F, получим малую ось эллипса, равную 0,7d
Пусть, строится окружность, расположенная параллельно горизонтальной плоскости проекции
где большая ось AB перпендикулярна свободной оси (z) и малая ось CD. — затем, после построения осей эллипса: — проводим прямую O — 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; — из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; — соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O1, которая определяет центр дуги CE; — строим точку O2 симметричную O1, относительно центра эллипса — O; — на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси — OB; — из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; — соединив прямой линией точки K и O1 на пересечении ее с большой осью находим точку O3, являющуюся центром дуги BK; — точку P находим на пересечении прямой O2O3 с дугой радиусом O3B. P — точка сопряжения дуг QP и BP; — точке O3 симметрична относительно центра эллипса точка O4; — аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения.
Более просто выглядит построение окружности, расположенной параллельно горизонтальной плоскости проекции
Источник
Начертательная геометрия
Аксонометрические проекции окружности
Окружность в аксонометрической проекции представляет собой эллипс, Построение эллипса сравнительно сложно, поэтому его заменяют овалом. Овал — это кривая, по очертанию похожая на эллипс, но строится при помощи циркуля.
Окружность в прямоугольной изометрии
Окружности, вписанные в грани куба ( рис 9.6а ), проецируются в эллипсы, В прямоугольной изометрии все три эллипса одинаковы по форме, равны друг другу, но расположены различно (рис 9.6.б) . Их малые оси всегда располагаются по направлению отсутствующей в данной плоскости аксонометрической оси, а большая ось к ней перпендикулярна.
Существует несколько способов построения окружности в
Первый способ. Строят ромб со стороной, равной D окружности. Точки А и В — центры больших дуг радиуса R, Точки С и Е — центры малых дуг радиуса г. Точки 1, 2, 3. 4 — точки сопряжения дуг (рис 9.7а ).
Второй способ. Проводят две окружности, одна — диаметром, равным большой оси овала (АВ = 1,22 D), вторая — диаметром, равным малой оси (СЕ = 0,71 D). Точки Oi и Oi — центры больших дуг овала, а точки Оз и 04 — центры малых дуг. Точки 1, 2, 3, 4 — точки сопряжения дуг (|рис 9.7i, б).
На рис 9-8 показан графический способ определения большой и малой осей изометрического эллипса. Для определения малой оси эллипса соединяем точки 1 и 2. Отрезок 1 — 2 — малая ось эллипса. Из точек 1 и 2, как из центров, описываем дуги радиусом 1 — 2 до их взаимного пересечения. Отрезок 3 — 4 — большая ось эллипса.
Окружность в прямоугольной диметрии
В прямоугольной диметрической проекции так же, как в прямоугольной изометрии, малые оси всех трех эллипсов расположены по направлению той аксонометрической оси, которая отсутствует в плоскости, содержащей эллипс.
На рис.9.9 показаны эллипсы, принадлежащие отдельнмм координатным плоскостям, и указаны размеры их осей. У эллипса, расположенного в плоскости x’0’z’, большая ось равна 1,06 D., малая — 0,94 D.
Эллипсы, принадлежащие координатным плоскостям x ¢ О ¢ y ¢ и z’Oy’ по величине и форме одинаковы. Большие оси этих эллипсов равны 1,06 D, малые — 0,35 D.
На риc.9.9 дано построение диметрического овала для окружности диаметра D, расположенной в плоскости x’O ¢ z ¢
Проводят оси диметрической проекции x ¢ y ¢ z ¢ , затем через точку О проводят прямую, перпендикулярную к оси у’, и на ней откладывают большую ось эллипса АВ. Малую ось эллипса CD откладывают на оси у! Отрезки ОМ = ON = OK = ОЕ равны радиусу данной окружности. Точки М, N, К и Е будут точками сопряжения дуг овала. Точки Oi, Oi, Оз и 04 будут центрами дуг радиусов окружностей, из которых состоит овал.
На рис.9.10 приведено построение диметрических овалов, заменяющих эллипсы, для окружностей, расположенных в плоскостях Н и W, Эти овалы одинаковы по форме и величине. Малая ось имеет направление той аксонометрической оси, которая отсутствует в плоскости, содержащей эллипс, большая ось к ней перпендикулярна.
Последовательность построения такая (рис 9.11, а): от центра О’ на продолжении малой оси эллипса откладываем размер 1,06 D (величину большой оси). Получаем точку O1- центр нижней дуги радиуса R, Из точки О2 этим же радиусом проводим верхнюю дугу овала. От точек А и В откладываем размеры малой оси, уменьшенной в четыре раза, т.е. EF / 4. Из полученных центров Оз, О4 проводим дуги радиуса R1= O’E/2. Точки сопряжения 5 и 6 находим, соединяя прямой точки O1 и О4(О2 и О4) и
продолжая эту прямую до пересечения с дугой.
Построение овала в плоскости W (рис 9.11 б) аналогично построению овала в плоскости Н.
9.4.3. Окружность в косоугольной фронтальной диметрии
На рис.9.12 изображен куб, выполненный в косоугольной фронтальной диметрии. В каждую грань куба вписана окружность. Одна из них, расположенная в плоскости V, проецируется без искажения; две другие — в виде эллипсов, где большая ось равна 1,07D, a малая — 0,33 D. Большие оси эллипсов перпендикулярны недостающим аксонометрическим осям плоскости, в которой они расположены.
Способ построения этих овалов такой же, как в прямоугольной диметрии.
9.5. Примеры построения стандартных аксонометрий
Аксонометрическую проекцию точки А строят по ее координатам ха, уa, za. На рис 9.13, а даны две проекции осей координат и точки. Чтобы построить изометрию точки, от точки О’ на оси х’ откладывают координату ха ( рис 9.13 б). Через полученную точку проводят прямую, параллельную оси у’ и откладывают на ней координату уА Отмечают вторичную проекцию А ¢ 1 точки А, затем откладывают координату za, параллельно оси z ¢ . Полученная точка А — изометрическая проекция точки. Итак, любую аксонометрическую проекцию точки можно получить, построив в аксонометрии трехзвенную координатную ломаную линию, определяющую положение этой точки относительно начала координат.
Аксонометрические проекции прямых, кривых строят по координатам их точек. На рис 9.14 показано построение отрезка АВ, на рис 9.15 показано построение плоской кривой, а на рис 9.16 — пространственной кривой в изометрической проекции
Построение шестигранной призмы по данному чертежу начинают с плоской фигуры основания (рис 9.171). Основание призмы строят по координатам его точек. На изометрической оси г’ откладывают высоту Н, проводят линии, параллельные осям х ‘и у.’ Отмечают на линии, параллельной оси х,’ положение точек 1 и 4.
Для построения точки 2 определяют координаты этой точки на чертеже — х2; и у2; и, откладывая эти координаты на аксонометрическом изображении, строят точку 2. Таким же образом строят точки 3, 5 и 6.
Построенные точки верхнего основания соединяют между собой. Боковые ребра призмы являются горизонтально — проецирующими
прямыми, поэтому на горизонтальную плоскость проекции Н они проецируются в виде точек. Из точки 1 проводят ребро до пересечения с осью х! затем — ребра из точек 2, 3, 6. Нижнее основание призмы проводят параллельно верхнему. Невидимые ребра призмы следует проводить штриховой линией.
Построение аксонометрической проекции прямого кругового конуса начинают с его основания (рис 9.18).
Аксонометрической проекцией основания будет эллипс, расположенный в плоскости Н. Далее из центра эллипса откладывают высоту конуса. Полученную точку — вершину конуса — соединяют двумя касательными с основанием. На | рис9.18а дано изображение конуса в прямоугольной изометрии, на рис.9.18 б — в прямоугольной диметр ии.
Прямоугольной аксонометрической проекцией сферы диаметром D является окружность, диаметр которой равен 1,22 D (изометрия) или 1,06 D (диметрия) по приведенным коэффициентам искажения. На рис.9.19 а изображена прямоугольная изометрия сферы с вырезом одной восьмой его части. На рис.9-19, б — прямоугольная диметрия сферы с вырезом одной восьмой его части. Три эллипса на изображении — проекции сечения шара координатными плоскостями.
На рис.9.20 изображена прямоугольная диметрия части тора. Сначала строят ось поверхности в виде овала, затем радиусом образующей сферы проводят окружности, равномерно располагая их по направляющей.
Для изображения кольца проводят плавную касательную ко всем окружностям. Чтобы спроецировать любую поверхность вращения (рис.9.21) вписывается в неё произвольные сферы, при этом 0 ¢ 1 ¢ =0 ² 1 ² и т.д. Плавная касательная ко всем окружностям представляет собой контур изображения .При построении ксонометрии по приведенным показателям искажения радиусы вписываемых сфер увеличиваются в изометрии в 1,22 раза, в диметрии — в 1,06
Источник
Аксонометрические проекции окружностей способы построение овала
При параллельном проецировании окружности на какую-нибудь плоскость П* получаем ее изображение в общем случае в виде эллипса (рис. 157).
Как бы ни была расположена плоскость окружности, сначала целесообразно построить параллелограмм A*B*C*D* – параллельную проекцию квадрата ABCD , описанного около данной окружности, а затем с помощью восьми точек и восьми касательных вписать в него эллипс.
Точки 1, 3, 5 и 7 – середины сторон параллелограмма. Точки 2, 4, 6 и 8 расположены на диагоналях так, что каждая из них делит полудиагональ в соотношении 3:7.
Из восьми касательных к эллипсу первые четыре – это стороны параллелограмма, а остальные t2, t4, t6 и t8– прямые, параллельные его диагоналям. Так касательная t2 * к эллипсу параллельна диагонали C*D* , Объясняется это тем, что t2 * и C*D* являются проекциями двух параллельных прямых t2 и CD .
 |  |
| Рисунок 157. Проецирование окружности на плоскость | |
Графические построения, предшествующие вычерчиванию самого эллипса, целесообразно выполнять в следующей последовательности (рис.158):
Рисунок 158. Построение эллипса
построить аксонометрическую проекцию квадрата — параллелограммA*B*C*D* и провести диагонали A*C* и B*D* ;
на отрезке 3*B* , как на гипотенузе, построить прямоугольный равнобедренный треугольник 3*KB* ;
из точки 3* радиусом 3*K описать полуокружность, которая пересечет A*B* в точках L и M ; эти точки делят отрезок 3*A* и равный ему отрезок 3*B* в отношении 3:7 ;
через точки L и М провести прямые параллельные боковым сторонам параллелограмма, и отметить точки 2*, 4*, 6* и 8* расположенные на диагоналях;
получив восемь точек и столько же касательных, можно с достаточной точностью вычертить эллипс.
ГОСТ 2.317-69 определяет положение окружностей, лежащих в плоскостях, параллельных плоскостям проекций для прямоугольной изометрической проекции (рис.159) и для прямоугольной диметрии (рис.160).


Рисунок 159. Изометрические проекции окружностей,
расположенных в плоскостях параллельных плоскостям проекций
Рисунок 160. Диметрические проекции окружностей,
расположенных в плоскостях параллельных плоскостям проекций
Если изометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось -0.71 диаметра окружности.
Если изометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось ось эллипсов 1, 2, 3 равна диаметру окружности, а малая — 0.58 диаметра окружности.
Если димметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 — 0.95, эллипсов 2 и 3 — 0.35 диаметра окружности.
Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 — 0.9, эллипсов 2 и 3 — 0,33 диаметра окружности.
1-эллипс (большая ось расположена под углом 90 0 к оси y); 2-эллипс (большая ось расположена под углом 90 0 к оси z); 3-эллипс (большая ось расположена под углом 90 0 к оси x).
Источник