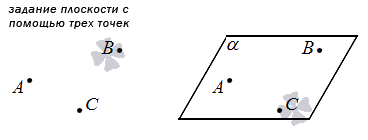- Плоскость в пространстве – необходимые сведения
- Понятие плоскости и ее обозначения
- Как могут располагаться плоскость и точка друг относительно друга
- Варианты взаимного расположения прямой и плоскости
- Варианты расположения двух плоскостей друг относительно друга
- Как задать плоскость в пространстве
- Способы задания плоскости в пространстве
- Аксиомы стереометрии
- Описание презентации по отдельным слайдам:
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Общая информация
- Похожие материалы
- Перспектива
- Изделия из теста
- Янтарная комната
- Искусство вазописи
- Я нарисую красками Судьбу
- Русская народная вышивка
- Эстетическая деятельность
- О самураях
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Безлимитный доступ к занятиям с онлайн-репетиторами
- Подарочные сертификаты
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
Прямые и точки, размещенные в пространстве, мы будем обозначать аналогично размещенным на плоскости – с помощью строчных и прописных латинских букв ( B , A , d , q и др.) Если в условиях задачи у нас есть две точки, которые расположены на прямой, то можно выбрать такие обозначения, которые будут соответствовать друг другу, например, прямая D B и точки D и B .
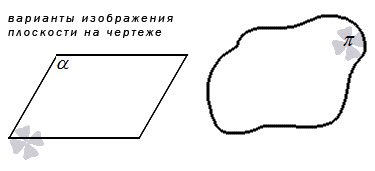
Чтобы обозначить плоскость на письме, традиционно используются маленькие греческие буквы, например, α , γ или π .
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Такой вариант расположения также называется прохождением плоскости через точку. Чтобы обозначить это на письме, используется символ ∈ . Так, если нам нужно записать в буквенном виде, что через точку A проходит некая плоскость π , то мы пишем: A ∈ π .
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Зная это правило, можно ввести новое обозначение плоскости. Вместо маленькой греческой буквы мы можем использовать названия точек, лежащих в ней, например, плоскость А В С .
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
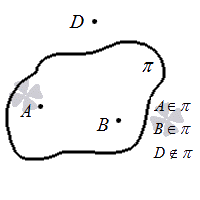
Выше мы уже отмечали, что для обозначения плоскости в пространстве будет достаточно трех точек, а четвертая может находиться как в ней, так и вне ее. Если нужно обозначить отсутствие принадлежности точки к заданной плоскости на письме, то используется знак ∉ . Запись вида A ∉ π правильно читается как «точка A не принадлежит плоскости π »
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
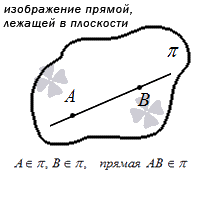
Чтобы записать принадлежность прямой некой плоскости, используем тот же символ, что и для точки. Если мы напишем « a ∈ π », то это будет означать, что у нас есть прямая a , которая расположена в плоскости π . Изобразим это на рисунке:
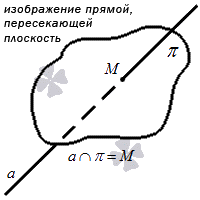
Второй вариант взаимного расположения – это когда прямая пересекает плоскость. В таком случае у них будет всего одна общая точка – точка пересечения. Для записи такого расположения в буквенном виде используем символ ∩ . Например, выражение a ∩ π = M читается как «прямая a пересекает плоскость π в некоторой точке M ». Если у нас есть точка пересечения, значит, у нас есть и угол, под которым прямая пересекает плоскость.
Графически этот вариант расположения выглядит так:
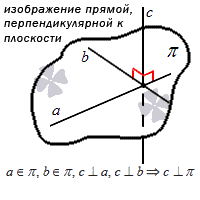
Если у нас есть две прямые, одна из которых лежит в плоскости, а другая ее пересекает, то они являются перпендикулярными друг другу. На письме это обозначается символом ⊥ . Особенности такой позиции мы рассмотрим в отдельной статье. На рисунке это расположение будет выглядеть следующим образом:
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
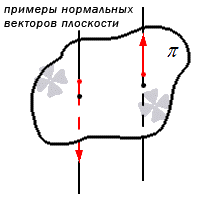
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
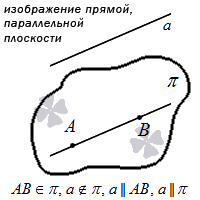
Третий случай взаимного расположения прямой и плоскости – это их параллельность. В таком случае ни одной общей точки у них нет. Для указания таких отношений на письме используется символ ∥ . Если у нас есть запись вида a ∥ π , то ее следует читать так: «прямая a является параллельной плоскости ∥ ». Подробнее этот случай мы разберем в статье про параллельные плоскости и прямые.
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
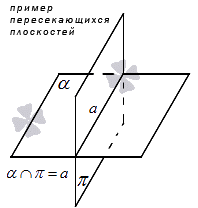
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
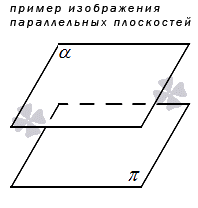
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
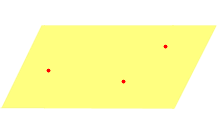
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
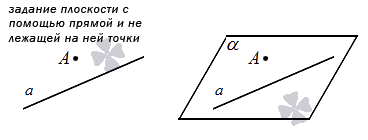
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
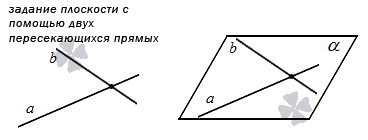
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
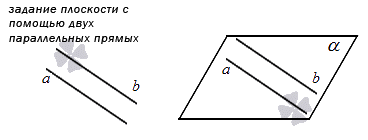
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
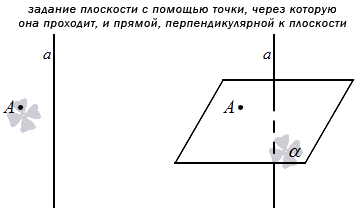
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
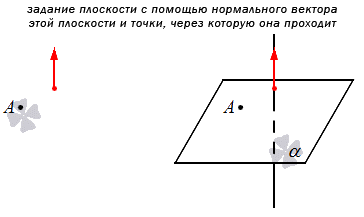
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.
Источник
Способы задания плоскости в пространстве
Все возможные способы задания плоскости в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка |
| Три различные точки | 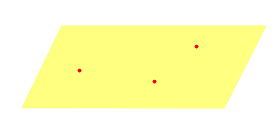 | |
| Прямая линия и точка, не лежащая на этой прямой | 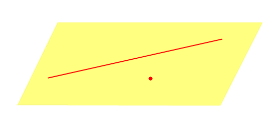 | |
| Две пересекающиеся прямые | 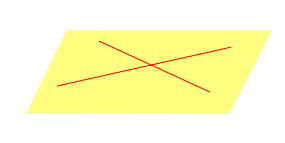 | |
| Две параллельные прямые | 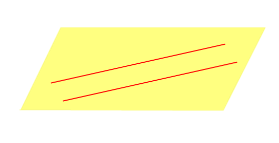 | |
| Прямая линия и точка, не лежащая на этой прямой | ||