Лекция на тему: «Аксиомы стереометрии. Следствия из них. Взаимное расположение прямых в пространстве.»
Аксиомы стереометрии. Следствия из них. Взаимное расположение прямых в пространстве.
Понятие геометрии как науки, геометрической фигуры, стереометрии.
Основные фигуры в пространстве.
Аксиомы стереометрии и их следствия .
Геометрия – это наука, которая изучает свойства геометрических фигур.
Геометрическая фигура – это любая совокупность точек.
Геометрия подразделяется на планиметрию и на стереометрию , которую мы начинаем изучать.
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Мы начнем изучение стереометрии с основных понятий, основных фигур, аксиом, точно также как это делалось в планиметрии.
Основные фигуры в пространстве: точки, прямые и плоскости.
Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д.
Плоскость.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
На рисунке плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д.
Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,
Основные свойства точек , прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах :
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются. А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Следствие 1. Через прямую a и не лежащую на ней точку A проходит плоскость, и притом только одна.

рис. 9
Следствие 2. Через две пересекающиеся прямые a и b проходит плоскость, и притом только одна.
Решение задач
Дан тетраэдр АВСD (Рис. 11). Даны следующие точки: точка Е – внутренняя точка ребра АВ , точка Р – внутренняя точка отрезка ЕD , точки М и К , соответственно, на ребрах ВD и DС .
Задача 1
а) В какой плоскости лежит прямая
Ответ: 
б) В какой плоскости лежит прямая
Ответ: 
в) В каких плоскостях лежит прямая
Ответ: Прямая BD лежит в плоскости BDА и в плоскости BDС . Значит, прямая BD одновременно лежит в двух плоскостях. Прямая BD есть линия пересечения двух плоскостей. Говорят, что грани АBD, BDС пересекаются по прямой BD . Это можно записать так:
г) В каких гранях лежит прямая 
Ответ: Прямая АB лежит в грани АВС и в грани АBD . Значит, прямая АВ есть линия пересечения двух этих граней.
д) В каких гранях лежит прямая 
Ответ: Прямая EC лежит в плоскости АВС и в плоскости ECD, так как точки Е и С лежат одновременно в плоскости АВС и в плоскости ECD. Значит, прямая ЕС есть линия пересечения этих плоскостей.
Задача 2.
а) Найдите точку пересечения прямой DК с плоскостью АВС .
Прямая DК содержит точку С . Плоскость АВС содержит точку С . Значит, прямая DК и плоскость АВС пересекаются в точке С .
б) Найдите точку пересечения прямой СЕ с плоскостью АDВ .
Точка Е принадлежит и прямой СЕ , и плоскости АDВ . Значит, Прямая СЕ пересекается с плоскостью АDВ в точке Е .
Задача 3.
а) Найдите точки, лежащие одновременно в плоскостях АDВ и DВС .
Точка В и точка D одновременно лежат и в АDВ , и в DВС . Значит, 
б) Найдите прямые, по которым пересекаются плоскость АDВ и DВС .
Точка В и точка D одновременно лежат и в АDВ , и в DВС . Значит, прямая DВ есть прямая, по которой пересекаются заданные плоскости.
в) Назовите прямые, по которым пересекаются плоскости АDВ и СDА .
Точки А , D лежат в плоскости АDВ , а также точки А , D лежат в другой плоскости СDА . Значит, АD – линия их пересечения: 
г) Назовите прямые, по которым пересекаются плоскости РDС и АВС .
Плоскость РDС совпадает с плоскостью ЕDС . Точка Е и точка С одновременно лежат в двух плоскостях: РDС и АВС . Значит, СЕ – это линия пересечения двух плоскостей. 
Вопросы для самоконтроля:
Дать определение геометрии.
Дать определение стереометрии?
Какие основные фигуры в пространстве вы знаете?
Как обозначаются основные фигуры в пространстве (точка, прямая, плоскость)?
Приведите примеры стереометрических фигур?
Какие аксиомы стереометрии и следствия из них вы знаете?
1. Перечислите известные вам аксиомы стереометрии.
2. Дан куб 
В каких плоскостях лежат прямые:
3. Назовите прямые, по которым пересекаются плоскости:
Источник
Аксиомы стереометрии и их следствия
Аксиомы стереометрии и их следствия
| Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. |  |
| Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую). |  |
| Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются. | 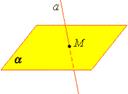 |
| Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты. |  |
3. Способы задания плоскости
· Плоскость в пространстве однозначно определяется:
· 3 точками, не лежащими на 1 прямой;
· прямой и точкой, не лежащими на 1 прямой;
· 2мя пересекающимися прямыми;
· 2мя параллельными прямыми.
· Каждое из заданий плоскости может быть преобразовано в другое из них.
4. Взаимное расположение прямой и плоскости в пространстве.
| Общие точки | Взаимное расположение | |
 | Более одной | Прямая лежит в плоскости |
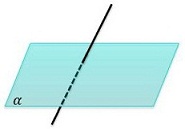 | Только одна | Прямая пересекает плоскость |
 | Ниодной | Прямая и плоскость параллельны |
Параллельные прямые в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
| Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. |  |
| Лемма о пересечении плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. |  |
| Теорема о трех прямых в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b). |  |
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
6. скрещивающиеся прямые
Признак скрещивающихся прямых.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
| 7.Признак параллельности прямой и плоскости Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. |  |
| Теорема. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Теорема.Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. | 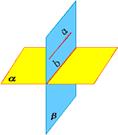 |
Параллельность плоскостей
Две плоскости параллельны, если они не имеют общих точек.
Однако в практических целях чаще используется признак параллельности плоскостей:
Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
13. Признак параллельных плоскостей:
- Если две плоскости параллельны третьей, то они параллельны друг другу.
- Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
- Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
14. Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.
Перпендикуляр и наклонная
Симметрия параллелограмма.
Большое число фигур обладает тем свойством, что при повороте плоскости чертежа на 180° вокруг некоторой точки новое положение фигуры совпадает с первоначальным. Такие фигуры называются центрально симметричными. Параллелограмм принадлежит к числу таких фигур, он центрально симметричен относительно точки пересечения его диагоналей (черт. 234).
В самом деле, так как ОС = ОВ и ОА = OD, то точки С и В, а также A и D симметричны относительно центра О. Если параллелограмм повернуть на 180° вокруг точки пересечения его диагоналей, то новое положение параллелограмма совпадёт с первоначальным.
Двугранный угол.
Определение. Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, и не принадлежащими одной плоскости.
 | а — ребро двугранного угла, полуплоскости — грани его. |
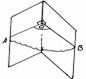 | Угол АОВ — линейный угол двугранного угла. Чтобы его построить, нужно выбрать произвольную точку О на ребре, а лучи ОА и ОВ должны быть перпендикулярны к ребру. |
Определение. Градусной мерой двугранного угла называется градусная мера любого из его линейных углов.
 | Двугранный угол называется прямым (острым, тупым), если он равен 90 o (меньше 90 o , больше 90 o ). Пусть  — тот из углов, который не превосходит любого из трёх остальных углов. Тогда угол между пересекающимися плоскостями равен — тот из углов, который не превосходит любого из трёх остальных углов. Тогда угол между пересекающимися плоскостями равен  . (0 o o ) . (0 o o ) |
Определение. Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 90 o .
· 40. Линейным углом двугранного угла называется угол, сторонами которого являются лучи, по которым грани двугранного угла пересекаются плоскостью, перпендикулярной ребру двугранного угла.
· У каждого двугранного угла сколько угодно линейных углов: через каждую точку ребра можно провести плоскость, перпендикулярную этому ребру; лучи, по которым эта плоскость пересекает грани двугранного угла, и образуют линейные углы.
· Все линейные углы двугранного угла равны между собой.
Коллинеарные векторы
Коллинеарные векторы это векторы, лежащие на параллельных прямых (или на одной и той же прямой).
 |  |
Векторы а, b, c коллинеарны. Векторы АС, BD, и СВ коллинеарны.
Коллинеарные векторы могут иметь одно и то же направление (равнонаправленные векторы) или противоположные.
Так, векторы а и с равнонаправлены, векторы а и b (а также b и c) противоположно направлены. Векторы АС и BD равнонаправлены, векторы АС и СВ противоположно направлены.
47. Компланарные векторы
Векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами.
Три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.
Всегда возможно найти плоскость, параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.
Eсли из трёх векторов два коллинеарны, то очевидно, что эти три вектора компланарны.
Правило треугольника
Сумма векторов a и b это третий вектор с, получаемый следующим построением: из произвольного начала О строим вектор OL, равный а; из точки L, как из начала строим вектор LM, равный b. Вектор с = ОМ есть сумма векторов a и b («правило треугольника»).
Правило параллелограмма
Если слагаемые a и b не коллинеарны, то сумму a + b можно найти следующим построением:
из любого начала О строим векторы ОА = а и ОВ = b; на отрезках ОА, ОВ строим параллелограмм ОАСВ. Вектор диагонали ОС = с есть сумма векторов a и b (так как АС = OB = b и ОС = ОА + АС).
Аксиомы стереометрии и их следствия
| Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. |  |
| Аксиома 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую). |  |
| Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются. |  |
| Аксиома 3. Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой. Пример: пересечение двух смежных стен, стены и потолка комнаты. |  |
3. Способы задания плоскости
· Плоскость в пространстве однозначно определяется:
· 3 точками, не лежащими на 1 прямой;
· прямой и точкой, не лежащими на 1 прямой;
· 2мя пересекающимися прямыми;
· 2мя параллельными прямыми.
· Каждое из заданий плоскости может быть преобразовано в другое из них.
4. Взаимное расположение прямой и плоскости в пространстве.
| Общие точки | Взаимное расположение | |
 | Более одной | Прямая лежит в плоскости |
 | Только одна | Прямая пересекает плоскость |
 | Ниодной | Прямая и плоскость параллельны |
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Источник


























