Абстрактный способ определения понятий

Определение через абстракцию.

Определения, связанные с выделением такого типа объектов через установление между ними отношений равенства, равнозначности, тождества, получили название определений через абстракцию. В таком определении данное математическое понятие определяется как семейство классов эквивалентности по некоторому отношению эквивалентности. Например, натуральное число n — это характеристика класса эквивалентных конечных множеств, состоящих из n элементов.

Остенсивные определения.

Остенсивныеопределения — определения значений слов путем непосредственного показа, демонстрации предметов. Часто применяются в начальной школе (понятия отрезка, окружности, угла и др.). Постепенно с развитием математического опыта и накоплением определенного числа понятий на смену остенсивным понятиям приходят вербальные понятия. Вербальныепонятия – это понятия, когда значения неизвестных выражений определяются через выражения, значения которых известны.

Определение называется корректным, если выполняются два условия:

а) отсутствует порочный круг и связанная с ним возможность исключения нововведенных терминов (“Решение уравнения — это то число, которое является его решением”);
б) отсутствует омонимия: каждый термин встречается не более одного раза в качестве определяемого.

Вопрос

Формой связи понятий друг с другом является суждение.Если суждения правильно отображают объективно существующие зависимости между вещами, то такие суждения называют истинными; в противном случае суждения будут ложными. Процесс получения нового суждения-вывода из одного или нескольких данных суждений называется умозаключением.Важнейшими видами сложных суждений являются теоремы и аксиомы (постулаты).

Аксиома(греч. — авторитетное предложение “то, что приемлемо”) —предложение, принимаемое без доказательства. Аксиомы и первичные (неопределяемые) понятия составляют основной фундамент математической теории.

К системе аксиом, характеризующих некоторую научную теорию, предъявляются требования независимости, непротиворечивости, полноты.

Постулат(лат. — требование) — предложение, в котором выражается некоторое требование (условие), которому должно удовлетворять некоторое понятие или некоторое отношение между понятиями.

При изучении свойств различных математических объектов приходится делать те или иные заключения, то есть на основе понятий и суждений того или иного раздела математики строить предложения, истинность которых необходимо обосновать.

Математическое предложение, истинность которого устанавливается посредством доказательства (рассуждения), называется теоремой.

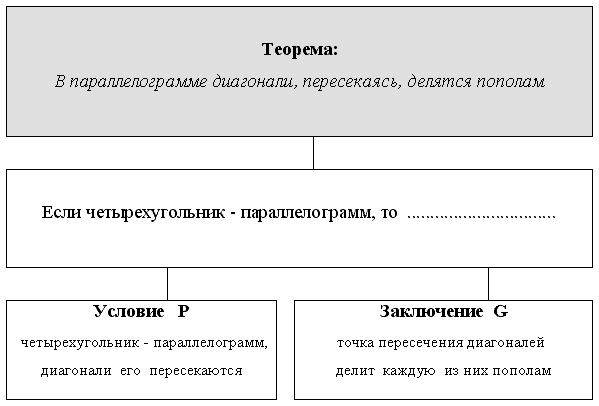
Существует два вида формулирования теоремы: условная, категорическая. Всегда можно из одного вида формулирования теоремы перейти в другому. Если теорема сформулирована в условной форме, то в ней должно быть ясно указано: при каких условиях рассматривается в ней тот или иной объект (условие теоремы) и что в этом объекте утверждается (заключение теоремы) (рис. 10).

Рис. 10. Структура теоремы

Доказательство теоремы состоит в том, чтобы показать, что если выполняется условие, то из него логически следует заключение, т. е., приняв, что Pистинно, в соответствии с правилами вывода показать, что Gистинно, и тем самым получить возможность утвердить, что данное высказывание (теорема) истинно в целом.

Доказательство включает в себя три основных элемента:

1. Тезис(главная цель доказательства — установить истинность тезиса). Форма выражения тезиса — суждение.

2. Аргументы(основания) доказательства — положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов — суждения. Связывая аргументы, приходим к умозаключению, которые строятся по определенным правилам. Аргументы, на которые можно опереться при доказательстве: аксиомы, определения, ранее доказанные теоремы.

3. Демонстрация —логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.

Известно, что имея некоторую (прямую) теорему ( P => G), можно образовать новые теоремы, и не одну:

G => P —обратная;
_ _
P => G —противоположная;
_ _
G => P —контрапозитивная (обратная противоположной или противоположнообратная).

Между этими четырьмя видами теорем существует тесная связь:
_ _
а) (P =>G)и (G => P) —одновременно истинны или ложны;
_ _
б) (G =>P)и (P => G) —одновременно истинны или ложны.

Изучая какую-либо теорему школьного курса математики, учитель должен придерживаться следующей последовательности:

1. Постановка вопроса (создание проблемной ситуации).

2. Обращение к опыту учащихся.

3. Высказывание предположения.

4. Поиск возможных путей решения.

5. Доказательство найденного факта.

6. Проведение доказательства в максимально простой форме.

7. Установление зависимости доказанной теоремы от ранее известных.

Процесс изучения школьниками теоремы включает следующие этапы: мотива­ция изучения теоремы; ознакомление с фактом, отраженным в тео­реме; формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы; усвоение содержания теоремы; запоми­нание формулировки теоремы; ознакомление со способом доказа­тельства; доказательство теоремы; применение теоремы; уста­новление связей теоремы с ранее изученными теоремами.

Источник

Определение через абстракцию

Большая советская энциклопедия. — М.: Советская энциклопедия . 1969—1978 .

Полезное

Смотреть что такое «Определение через абстракцию» в других словарях:

ОПРЕДЕЛЕНИЕ ЧЕРЕЗ АБСТРАКЦИЮ — определение абстрактных понятий как классов равных в каком либо смысле предметов; напр., понятие направления определяется как классы параллельных прямых и т. п … Большой Энциклопедический словарь

определение через абстракцию — определение абстрактных понятий как классов равных в каком либо смысле предметов; например, понятие направления определяется как классы параллельных прямых и т. п. * * * ОПРЕДЕЛЕНИЕ ЧЕРЕЗ АБСТРАКЦИЮ ОПРЕДЕЛЕНИЕ ЧЕРЕЗ АБСТРАКЦИЮ, определение… … Энциклопедический словарь

ОПРЕДЕЛЕНИЕ ЧЕРЕЗ АБСТРАКЦИЮ — способ выделения (абстрагирования) чувственно невоспринимаемых свойств предметов нек рой конкретной области исследования путем установления между предметами этой области отношений типа равенства. Напр., через обмениваемость товаров друг на друга… … Философская энциклопедия

ОПРЕДЕЛЕНИЕ ЧЕРЕЗ АБСТРАКЦИЮ — определение абстрактных понятий как классов равных в к. л. смысле предметов; напр., понятие направления определяется как классы параллельных прямых и т. п … Естествознание. Энциклопедический словарь

ОПРЕДЕЛЕНИЕ — дефиниция (лат. defenitio ограничение) логическая операция, раскрывающая содержание понятия. Напр., обычное определение термометра указывает, что это, во первых, прибор и, во вторых, именно тот, с помощью которого измеряется температура. Важность … Философская энциклопедия

ОПРЕДЕЛЕНИЕ, — ОПРЕДЕЛЕНИЕ, дефиниция (от лат. «definitio» – «предел», «граница») – логическая процедура придания строго фиксированного смысла терминам языка. Т.к. значения терминов зависят от их смыслов, то всякий раз, придавая через определение какой либо… … Философская энциклопедия

Определение (объяснение значения) — Определение, дефиниция (от лат. definitio), указание или объяснение значения (смысла) термина и (или) объёма (содержания) выражаемого данным термином понятия; этот термин (понятие) называется определяемым (лат. definiendum, сокращенно Dfd), а… … Большая советская энциклопедия

Определение — I Определение дефиниция (от лат. definitio), указание или объяснение значения (смысла) термина и (или) объёма (содержания) выражаемого данным термином понятия (См. Понятие); этот термин (понятие) называется определяемым (лат. definiendum … Большая советская энциклопедия

ОПРЕДЕЛЕНИЕ, или ДЕФИНИЦИЯ — (от лат. difinitio) логическая операция раскрытия содержания понятия. О. понятия, т. е. обнаружение его предела (границы), связано с нахождением существенных свойств предметов, отображаемых данным понятием. Структурно О. представляет собой… … Современный философский словарь

АБСТРАКЦИЯ — (от лат. abstractio отвлечение, отделение) процесс мысленного отвлечения одних свойств и отношений вещей и явлений от других. А. отождествления выделяет общее свойство объектов путем установления отношения эквивалентности или равенства между ними … Философская энциклопедия

Источник

Абстракция — что это такое и как абстрактное мышление (абстрагирование) помогает увидеть суть

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Вспомните скучные уроки в школе или университете, на которых вам хотелось спать. Что в них было общего? Обилие научных понятий, общих тезисов (что это такое?) и размытых формулировок.

Вводный теоретический урок предполагает работу с абстракциями. Из-за них он такой обобщённый, как бы оторванный от предмета.

Что такое абстракция? Зачем она нужна? И как она связана с другими сложными понятиями: абстрагированием, абстрактным мышлением? В этой статье мы разберём все вопросы по полочкам. Поехали!

Абстракция и абстрагирование — это упрощение реальности

Абстракция – это мысль, которая родилась в процессе абстрагирования (процесса исключения и отделения несущественного в данный момент, чтобы увидеть главное). Разочарованный читатель, наверное, подумал: «Ну вот, опять нет чёткого определения, а только размытая фраза». Наберитесь терпения, до истины (что это?) осталось совсем чуть-чуть.

У слова «abstractio» три варианта перевода с латыни:

Это мыслительные операции, которые проводит мозг над объектами реального мира в процессе абстрагирования. И появляются абстракции.

Вот несколько примеров для понимания.

Вы вышли на улицу и посмотрели вверх. О чём подумали? «Газовая оболочка из пяти слоёв с водяным паром, содержит 78% азота, 21% кислорода и так далее». Да так и с ума сойти можно!

Чтобы этого не произошло, вы отвлекаетесь от несущественных сторон, свойств и связей объекта. Выбрасываете из головы слои атмосферы, химический состав и формируете общую мысль – «небо».

Так вот, «небо» — это и есть абстракция. Вы можете пойти дальше и выделить другие существенные признаки объекта: цвет, погоду, время суток. Тогда возникнут такие абстрактные понятия: «голубое небо», «пасмурное небо», «ночное небо».

В конце месяца вы сняли с банковской карты зарплату. Теперь ваша общая мысль – «деньги». Это тоже абстракция. В процессе абстрагирования вы мысленно исключили (отделили) несущественные связи объекта.

Например, связи с банковским учреждением и работодателем. Разве вам интересно, какой длинный путь прошли титульные знаки перед тем, как оказались в вашем кошельке? Вряд ли. Важно то, что это деньги.

Таким образом, вы постоянно занимаетесь абстрагированием и порождаете абстракции. Без этого процесса голова бы просто лопнула от мыслей.

Тогда почему так трудно высидеть на скучных лекциях?

Абстрактные понятия — это высшая форма абстракции

Обобщать можно не только объекты реального мира, но и сами абстракции. Так формируются абстракции высокого порядка – абстрактные понятия. Ими оперируют фундаментальные и точные науки, чтобы описывать сложные закономерности.

Рассмотрим упрощённый пример того, как рождается абстрактное понятие.

На землю выпали атмосферные осадки из кристалликов льда. Это снег. Небо полностью закрыто облаками. Небо и снег белые. На улице белизна.

«Белизна» — это абстрактное понятие. Попробуйте его обобщить. Не получится. Другие примеры абстрактных понятий: истина, справедливость, время, вещество, информация.

От простой абстракции до её высшей формы иногда проходит так много мыслительных этапов, что абстрактное понятие оказывается сильно оторванным от реальности и сложным для восприятия.

Поэтому так трудно слушать теоретические лекции преподавателя.

Виды абстракций

Абстрагирование – это мыслительный процесс, который преследует определённую цель. Вычленить какой-то существенный признак, получить общую картину явления или выработать идеальную схему.

В зависимости от цели абстрагирования выделяют три вида абстракций.

1. Изолирующая.
   Цель – выделить существенный признак объекта и сосредоточить на нём внимание. На столе лежит апельсин. Вы замечаете, что фрукт оранжевый или сладко-кислый.
2. Обобщающая.

Цель – получить общую картину явления. Для этого вы отвлекаетесь от частных признаков. Пример обобщающей абстракции – это математические уравнения. Они решаются по определённым правилам. Нет смысла мысленно «дробить» математические уравнения на цифры, плюс, минус, знак равенства, переменную.

Вы, наверное, замечали, что успех в решении любой математической задачи зависит от умения посмотреть на проблему как бы сверху, увидеть общую картину.
Идеализация.

Цель – выработать идеализированную схему объекта, отбросив несущественные реальные атрибуты. Идеализация – это метод познания, без которого не обходятся точные и естественные науки. Вспомните пресловутого «сферического коня в вакууме».

В реальности нет изолированных точек, прямых линий, времени. В отрыве от конкретного объекта их нельзя потрогать, измерить. Это абстракции, которые используются в математике и физике для описания закономерностей реальных явлений.

Что такое абстрактное мышление

Если абстрагирование – это процесс выработки абстракций, то абстрактное мышление – это оперирование ими.

Строгий экзаменатор критикует молодого человека, отвечающего слишком пространно: «Давайте ближе к предмету билета».

Почему студент так бросается умными фразами? Чтобы скрыть пробелы в знаниях, а то и полное их отсутствие. И в этом кроется суть абстрактного мышления.

Знания человека о реальном мире не являются полными, исчерпывающими, конкретными. Но ему нужно как-то ориентироваться среди неизвестных явлений и вещей, поэтому он мыслит абстрактно.

Если бы не было понятия времени, то как бы люди договаривались о встречах? Как бы учёные описывали новые галактики, не имея представления о форме, расстоянии, скорости, веществах? А как бы без общих понятий взаимодействовали науки?

Абстрактное мышление – это форма познания, которая позволяет выйти из интеллектуального тупика, хотя бы на обобщённом уровне описать неизвестные явления. С его помощью строят догадки и видят проблему с разных углов.

Вы стали свидетелем семейной ссоры. Вашему другу на телефон звонит жена, плачет, кричит, ругается. Какие выводы делает мозг?

1. Конкретное мышление: жена друга – истеричка;
2. Абстрактное мышление: возможно, друг обижал жену, она долго терпела, но теперь не может сдерживать эмоции.

Краткое резюме

Итак, если говорить совсем уж простым языком, то термин, вынесенный в заголовок этой статьи, представляет из себя общую мысль, которая приближает нас к сути объекта (явления).

Абстракция – это посредник между человеком и сложным миром с его тайнами, законами.

Глупо противопоставлять конкретные понятия абстрактным, потому что без последних невозможен сам процесс познания.

Автор статьи: Наталья Белоусова

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (8)

Спасибо за развернутую и крайне понятную подачу материала, выручили!

Незнаю как поблагодарить за такое ясное определите слова . Вы просто супер.такими простыми словами объяснили. Спасибо искренне.

Так абстракция может быть реальным миром и нет? Ведь допустим такой пример : смотрю в книгу , вижу фигу-абстракция же?! Но она в реальном мире уже не существует (фига) -это образное высказывание , но по сути она же является абстракцией.

И ваш пример в начале статьи с небом -это уже реальность. Т.е. абстракция не обязательно должна быть реальна(существовать)? Как это сложно работает , но в целом мне ваша статья понравилась , спасибо , сделал некоторые пометки .

Автор статьи явно молодец.

Абстрактное мышление может быть очень полезно при решении любых задач, причем как теоретических, так и практических. Жаль только, что в школах и других учебных заведениях толком не учат правильным и эффективным методикам.

Мы можем мыслить абстрактно, чтоб объяснить для себя некоторые неосязаемые категории, однако дальше этого, навыки мышления идут редко.

Это всё здорово, но вот когда так называемый художник выплескивает на полотно свои абстрактные идеи, вот тут не по себе становится. Одно дело создание абстракции для решения задач, совсем же другое, когда абстракция создается ради самой абстракции или для подтверждения бредовых идей.

Источник