8 бит сколько способов

UTF-8 vs UTF-16. Несколько советов программистам

Введение

С появлением первых устройств цифровой передачи информации и электронно-вычислительных машин возникла задача кодирования текстовых символов с помощью последовательностей единиц и нулей. Минимальная единица представления информации – байт. Исходя их этого в 1963 году в США разработана, стандартизована, а впоследствии расширена кодовая таблица ASCII (American standard code for information interchange), использовавшая 8 битную кодировку. В первую очередь с помощью этой таблицы предполагалось кодирование цифр и букв английского языка. Первые 128 символов таблицы представлены на рис.1:

Рис.1. Первые 128 символов таблицы ASCII.

Номер ячейки в таблице (рис.1) является кодом символа. В качестве примера рассмотрим кодирование слова Hello. Номера ячеек таблицы ASCII, в которых размещены буквы: 72 (H), 101 (e), 108 (l), 111 (o). Код слова в бинарном представлении выглядит следующим образом:

00010010 (H) 10100110 (e) 00110110 (l) 00110110 (l) 11110110 (o) (старший бит справа).

Выделенные подчеркиванием и жирным коды в двоичном представлении соответствуют номерам ячеек в таблице (рис.1). Алгоритм формирования кода следующий:

1. Выделены жирным – биты управления кодированием (префикс). 010 – кодируется заглавная буква алфавита, 011 – строчная.

2. Выделены подчеркиванием – порядковые номера букв в английском алфавите.

Таким образом, с помощью первых 128 ячеек таблицы ASCII могли быть закодированы основные символы, цифры и буквы английского языка. Остальные 128 ячеек (8 битная кодировка позволяет закодировать 256 символов) могли использоваться для кодирования других языков. Однако, учитывая разнообразие символов и языков, 8 бит недостаточно.

Стандарт Юникод

Консорциум Unicode (Юникод) – некоммерческая организация, главной задачей которой являлась разработка стандарта кодирования (стандарт Юникод) с поддержкой наибольшего числа языков и символов служебного характера. Принцип кодирования на основе таблицы сохранился, а таблица (таблица Юникод) была значительно расширена.

Стандарт Юникод предоставляет пользователям таблицу Юникод и способы кодирования символов.

Символы таблицы Юникод являются элементами «универсального набора символов» UCS (Universal Coded Character Set), определенного международным стандартом ISO/IEC 10646. Таблица Юникод каждому символу UCS сопоставляет кодовую точку, которая является номером ячейки таблицы, содержащей символ.

Способы кодирования символов таблицы Юникод, т.е. преобразования номеров ячеек таблицы Юникод в бинарные коды, составляют кодовое пространство, состоящее из трех кодов семейства UTF (Unicode Transformation Format): UTF-8, UTF-16 и UTF-32

UTF-8 – стандарт кодирования, преобразующий номера ячеек таблицы Юникод в бинарные коды с использованием переменного количества бит: 8, 16, 24 или 32.

UTF-16 – стандарт кодирования, преобразующий номера ячеек таблицы Юникод в бинарные коды с использованием переменного количества бит:16 или 32.

Коды UTF-8 и UTF-16 используют разные алгоритмы кодирования набора символов UCS.

Стандарт кодирования UTF-8

Стандарт закреплен в RFC (Request For Comments) 3629. Алгоритм кодирования согласно RFC:

0xxxxxxx

110xxxxx 10xxxxxx

1110xxxx 10xxxxxx 10xxxxxx

11110xx 10xxxxxx 10xxxxxx 10xxxxxx

Старший бит слева. Началом кода является управляющий символ (выделен жирным):

0 – используется 8-битная кодировка,

110 – используется 16-битная кодировка,

1110 – используется 24-битная кодировка,

11110 – используется 32 битная кодировка.

В начале каждого последующего байта – биты 10 – управляющий символ (выделен подчеркиванием), означающий продолжение кодирования.

Первые 128 ячеек таблицы Юникод повторяют таблицу ASCII. Для кодирования заглавных и строчных букв русского алфавита используются ячейки с номерами 1040-1103.

Рассмотрим пример кодирования фразы «Папа Hello».

Код в бинарном виде (старший бит справа):

00001011 11111001 (П) 00001011 00001101 (а) 00001011 11111101 (п) 00001011 00001101 (а) 00000100 (пробел) 00010010 (H) 10100110 (e) 00110110 (l) 00110110 (l) 11110110 (o).

Букве П русского алфавита согласно таблицы Юникод соответствует номер 1055, в бинарном представлении 10000011111 – 11 бит. Соответственно данный символ может быть закодирован двумя байтами с использованием префикса 110 – для первого байта и 10 – для второго байта. Английские буквы слова Hello кодируются 1 байтом, а коды совпадают с кодами в таблице ASCII.

Основными преимуществами способа кодирования UTF-8 являются многообразие символов, которые могут быть закодированы, а также возможность кодирования переменным количеством бит, что позволяет сэкономить количество информации, передаваемое в канале связи.

Стандарт кодирования UTF-16

В феврале 2000 года опубликован документ RFC 2781, в котором закреплен стандарт UTF-16, позволяющий кодировать символы таблицы Юникод с помощью 16 или 32 битных значений. Символы с номерами 0-55295 и 57344-65535 кодируются с помощью 16 бит без изменений (без использования префиксов), а остальные символы, номера которых в двоичном представлении формируются количеством бит больше 16, кодируются 32 битами с использованием специального алгоритма. Рассмотрим пример кодирования фразы «Папа Hello».

Код в бинарном виде (старший бит справа):

11111000 00100000 (П) 00001100 001000000 (а) 11111100 00100000 (п) 00001100 001000000 (а) 00000100 00000000 (пробел) 00010010 00000000 (H) 10100110 00000000 (e) 00110110 00000000 (l) 00110110 00000000 (l) 111110110 00000000 (o).

Номера букв русского и английского алфавитов таблицы Юникод передаются без изменений при помощи 16 бит, старшие незначащие биты принимают нулевое значение.

Рассмотрим подробнее алгоритм кодирования символов, номера которых превышают значение 65535. Для примера в качестве символа используем букву древнетюркского алфавита, представленную на рис.2:

Рис.2. Буква древнетюркского алфавита.

Номер предложенного символа в таблице Юникод – 68620 (0х10COC).

Алгоритм преобразования номера символа в код UTF-16 состоит из нескольких шагов:

Из значения номера символа вычесть число 0х10000. Данная операция позволяет привести размерность бинарного представления номера символа к 20 битам. Для предложенного символа получим: 0х10COC – 0x10000 = 0xC0C.

Для полученного значения выделить старшие 10 бит и младшие 10 бит. В примере число 0хС0С в бинарном виде представляется, как 00000000110000001100, где жирным выделены 10 старших бит, а подчеркиванием – 10 младших.

К шестнадцатеричному значению 0xD800 (11011000 00000000) прибавить значение 0х03 (00000000 00000011), сформированное 10 старшими битами, полученными на предыдущем шаге. 0xD800 + 0х03 = 0хD803 (11011000 00000011) – 16 старших бит кодового слова UTF-16.

К шестнадцатеричному значению 0xDC00 (11011000 00000000) прибавить значение 0х0C (00000000 00001100), сформированное 10 младшими битами, полученными на шаге №2. 0xDС00 + 0х0С = DС0С (11011100 00001100) – 16 младших бит кодового слова UTF-16.

Кодовое слово UTF-16, соответствующее символу в примере, формируется из бит, полученных на шагах 3 и 4: 0хD803DC0C (11011000 00000011 11011100 00001100).

Сравнение стандартов UTF-8 и UTF-16 с точки зрения объема машинной памяти, используемой кодом для представления символов

Результаты сравнения стандартов представлены в таблице 1.

Таблица 1. Результаты сравнения стандартов.

В ячейках таблицы 1 содержится количество бит, требуемое для кодирования одного символа из таблицы Юникод. Видно, что для диапазонов номеров ячеек 128-2047, 65535-1048575 стандарты UTF-8 и UTF-16 используют одинаковое количество бит. Для диапазона 0-127 выгодно использование стандарта UTF-8, например, в случае, если программисту поручили реализовать кодер букв английского алфавита. Для диапазонов 2048-32767 и 32768-65535 выгодно использование стандарта UTF-16, например, в случае, если программисту поручили реализовать кодер иероглифов Бопомофо (занимают в таблице Юникод диапазон ячеек 12549-12589). Кодирование символов таблицы Юникод, расположенных в ячейках, номера которых начинаются от 1048575 возможно только с использованием кодировки UTF-16.

В предыдущих главах приведены примеры кодирования фразы «Папа Hello» стандартами UTF-8 и UTF-16. Кодировкой UTF-8 используются 14 байт, кодировкой UTF-16 20 байт, что связано с избыточностью кодирования англоязычных символов во втором случае из-за использования дополнительного байта 0х00. Можно сделать вывод, что для кодирования текста содержащего набор букв русского и английского алфавитов, предпочтительно использование кодировки UTF-8.

Вывод: в зависимости от языка алфавита может быть выбрана как кодировка UTF-8, так и кодировка UTF-16. Для английского алфавита однозначно более выгодно использование кодировки UTF-8, для русского алфавита буквы представляются одинаковым количеством бит при использовании как одной, так и другой кодировки.

Несколько советов программистам

Допустим, программист решил реализовать текстовый редактор, поддерживающий алфавит языка Бопомофо. Символы данного языка располагаются в таблице Юникод в диапазоне 12549-12589 и, следовательно, программисту необходимо выбрать стандарт UTF-16 для кодирования. Предположим, что для ввода символов решено использовать программную клавиатуру, состоящую из кнопок, каждая из которых соответствует букве алфавита языка. Кнопки – объекты класса button. Нажатие пользователем на какую-либо из кнопок порождает событие, в результате которого приложению становится известен номер ячейки таблицы Юникод. Программисту рекомендуется:

1.Хранить в памяти приложения символы таблицы Юникод и номера ячеек, соответствующие только языкам, поддержка которых планируется в текстовом редакторе. Это уменьшит объем памяти, занимаемой приложением, а также повысит скорость его работы, сузив область поиска номера ячейки.

2. При реализации приложения заранее выполнить преобразование всех номеров ячеек в их бинарные коды. Результат преобразования сохранить в файле, в формализованном виде. При загрузке приложения выполнить считывание в память номеров ячеек и их бинарных кодов UTF-16. Это позволит снизить вычислительную нагрузку приложения в ходе его работы.

3. Для хранения номеров ячеек и их бинарных кодов использовать объект класса, позволяющего осуществить это в виде ключ-значение, где ключ – номер ячейки, а значение – бинарный код. Классы, реализующие в языках программирования данный функционал, организуют работу таким образом, чтобы минимизировать время поиска ключа, используя сортировку ключей или хеширование.

Отметим проблему кодирования составных символов, которая является важным техническим аспектом. Например, символ ü может быть интерпретирован, как самостоятельный символ, которому соответствует номер ячейки 252 или может быть скомпонован из двух символов: u, которому соответствует номер ячейки 117 и символа ¨, которому соответствует номер ячейки 776. Программист должен строго придерживаться одного из вариантов представления таких символов иначе побайтовое сравнение строк будет невозможно. Рекомендуется использование второго варианта, который может облегчить поиск составных символов в тексте. Например, если пользователь осуществляет поиск символа u, то ему может быть выведен в качестве результата, как составной символ ü, так и самостоятельный u.

Источник

Бит | Байт | Системы счисления

Для полноты понимания работы микроконтроллера необходимо четко знать, что такое бит и байт, а также уметь применять различные системы счисления.

Основным вычислительным ядром любого микроконтроллера является микропроцессор. Именно он выполняет обработку команд или же кода, написанного программистом.

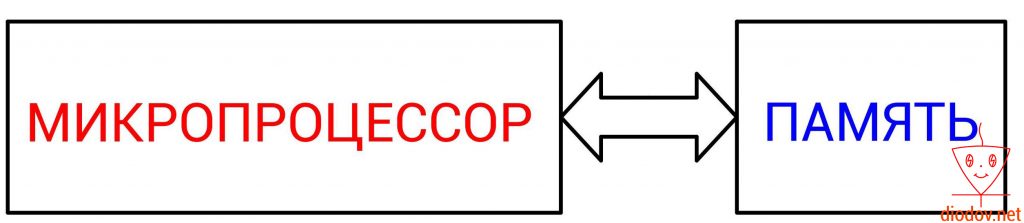
Упрощенно работу микропроцессора можно представить следующим образом. Сначала выполняется считывание данных из определенной ячейки памяти, далее выполняется их обработка и затем возвращение результата назад в ячейку памяти. Следовательно, для того, чтобы микропроцессор мог выполнять свои функции необходимо наличие памяти. Иначе ему неоткуда будет считывать данные, а затем некуда помещать результаты вычислений.

Давайте кратко рассмотрим алгоритм работы микропроцессора (МП) на примере сложения двух цифр.

1. Сначала МП считывает значение одного числа по указанному адресу ячейки памяти.
2. Далее он считывает другое значение из второй ячейки.
3. Складывает оба значения.
4. Возвращает их суму в ячейку памяти.

Вот такой монотонной работой занимаются микропроцессоры. Для выполнения одной команды ему необходимо выполнить четыре операции. Однако современные МП выполняют более 1 000 000 000 операций за одну секунду. Микроконтроллеры же выполняют более 1 000 000 операций, чего, как правило, предостаточно для такого крохотного устройства.

Данные, с которыми оперирует микропроцессор, представляют собой набор цифр. Поэтому нашей целью является рассмотреть, какие цифры, а точнее системы счисления “понимает” микроконтроллер.

Десятичная система счисления

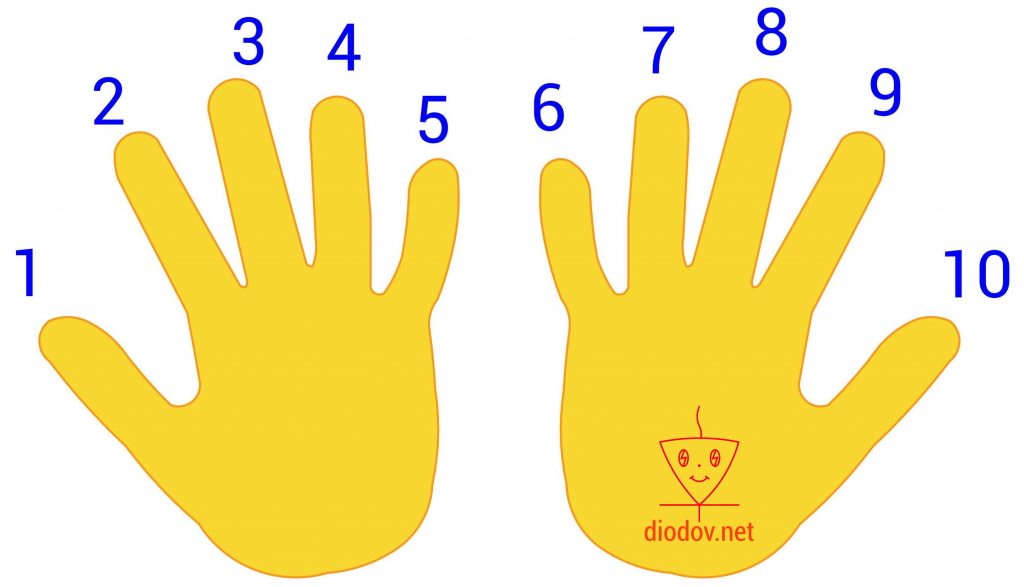
Десятичная система счисления нам очень близка и понятна. Возникла она очень давно, когда у людей впервые возникал необходимость подсчета чего-либо, например количества дней или определённых событий. Поскольку в те давние времена не было каких-либо технических устройств, то люди использовали для счета пальцы рук. Загибая или разгибая пальцы можно получить десять комбинаций, что очень просто и наглядно.

Математически данная она состоит из десяти разных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, поэтому она и называется десятичной. С помощью указанных символов легко отобразить любое число.

Основанием десятичной системы является 10. Когда при счете использованы все знаки от 0 до 9, то, чтобы продолжить дальнейший счет, необходимо вместо символа 9 поставить символ 0, т. е. обнулить предыдущее значение, а слева от нуля записать символ 1. И так можно продолжать счет до бесконечности, прибавляя слева от текущей позиции цифры последующую.

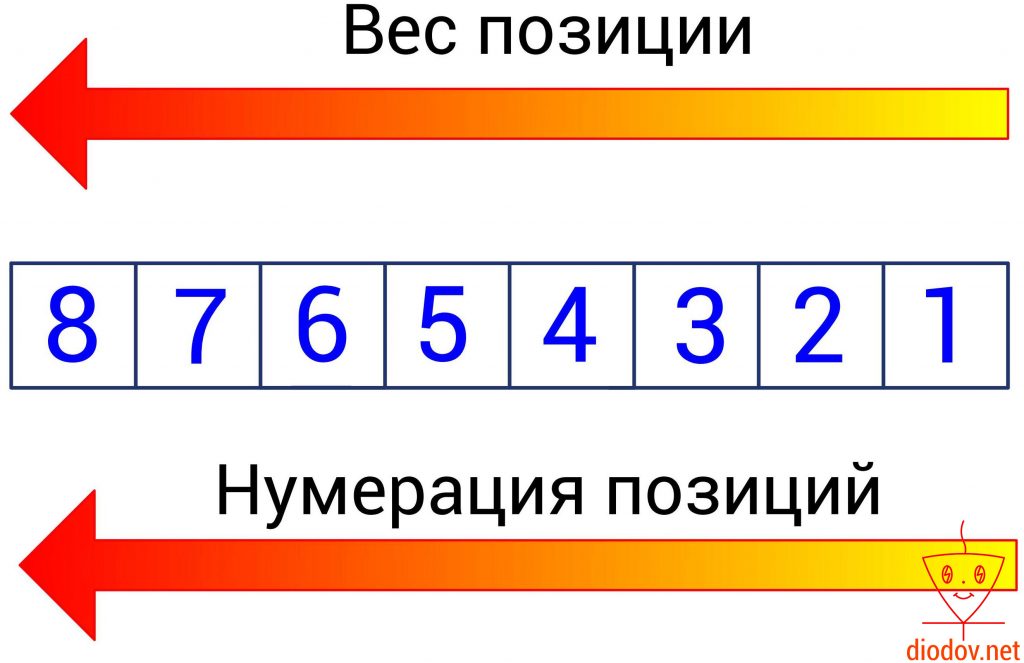
Каждая позиция цифры имеет свой вес. Наименьший вес имеет позиции, находящаяся в крайнем правом положении. По мере перемещения слева на право, вес позиции возрастает.

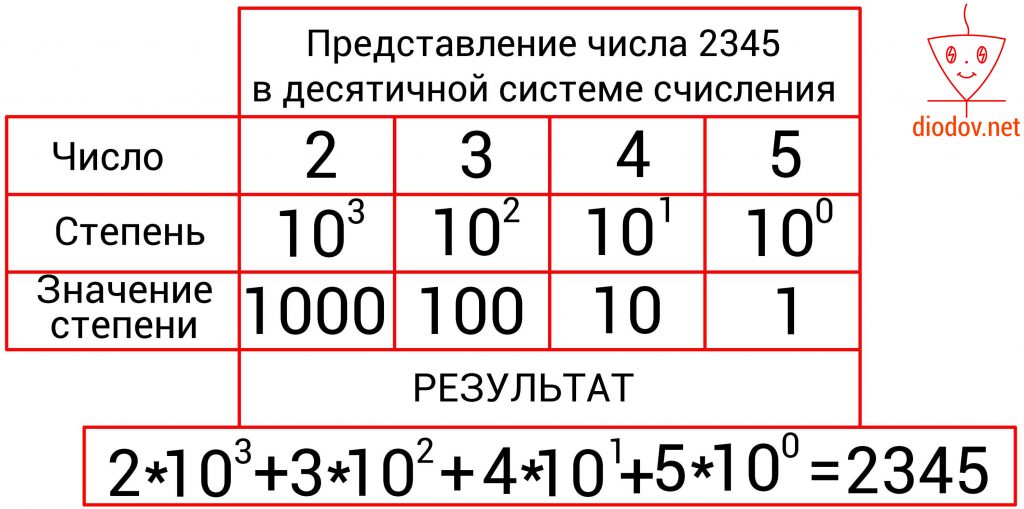
Например, число 2345 имеет 4 позиции. В крайней левой позиции отображаются единицы, в данном случае 5 единиц, а степень 10 имеет нулевое значение. Далее вес позиции увеличивается. Следующее значение, расположенное слева от предыдущего, уже содержит десятки, а 10 имеет степень 1, поэтому во второй позиции числа 2345 четыре десятка.

Далее перемещаемся по разрядам 2345 справа налево и увеличиваем степень 10 еще на одну единицу, т. е. имеем 10 2 . Соответственно получаем три сотни. И последняя цифра, она же первая по счету, если считать слева на право, имеет наибольший вес для, т. е. 10 3 , и поэтому имеем 2000. Чтобы получить окончательный результат, следует сложить количество значений цифр всех позиций.

Двоичная система счисления

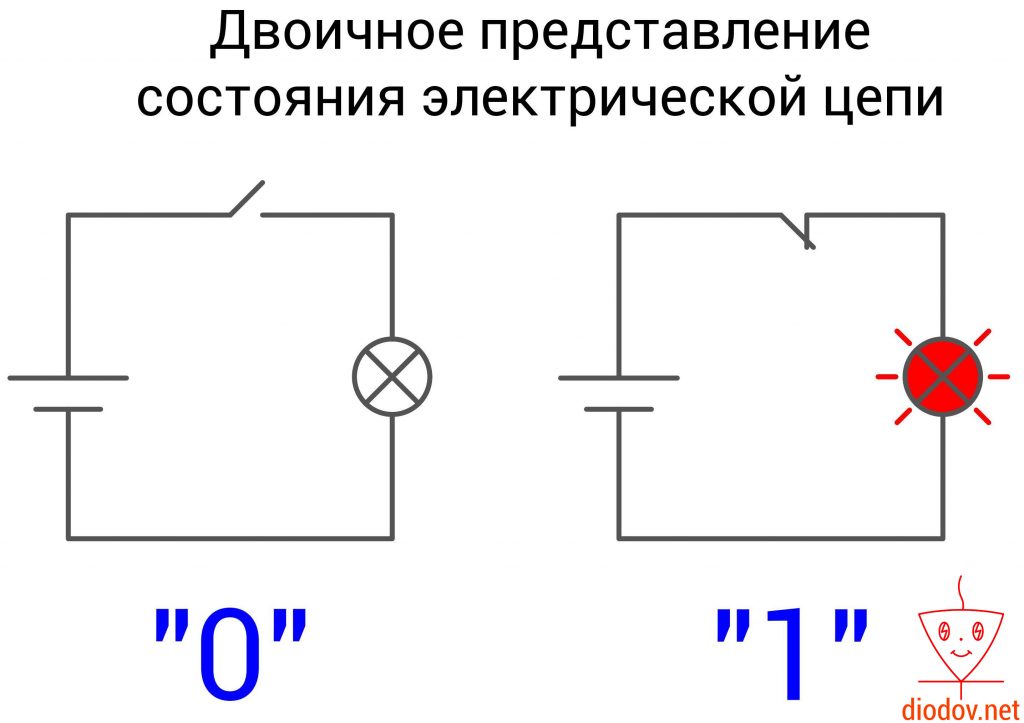
Двоичная система счисления оперирует всего лишь двумя символами 0 и 1. Она повсеместно применяется в цифровой технике, поскольку очень удачно сочетается с двумя устойчивыми состояниями электрической цепей: включено и выключено либо есть сигнал и нет сигнала. Также нулем еще обозначают сигнал низкого уровня, а единицей – высокого.

Порядок записи двоичного числа полностью соответствует десятичному. Веса позиций также возрастают справа налево. Только основанием является 2, а не 10.

Чтобы отличать двоичную систему от десятичной в цифровой технике используют индекс 2 и 10 соответственно:

1101₁₀ – десятичное.

При написании кода программы для обозначения двоичного значения перед ним ставится префикс 0b, например 0b11010101. Если записывается десятичное, то перед ним ничего не ставится.

0b11010101 – двоичное;

11010101 – десятичное.

Бит и байт

Двоичная система счисления также используется при хранении и обработке информации.

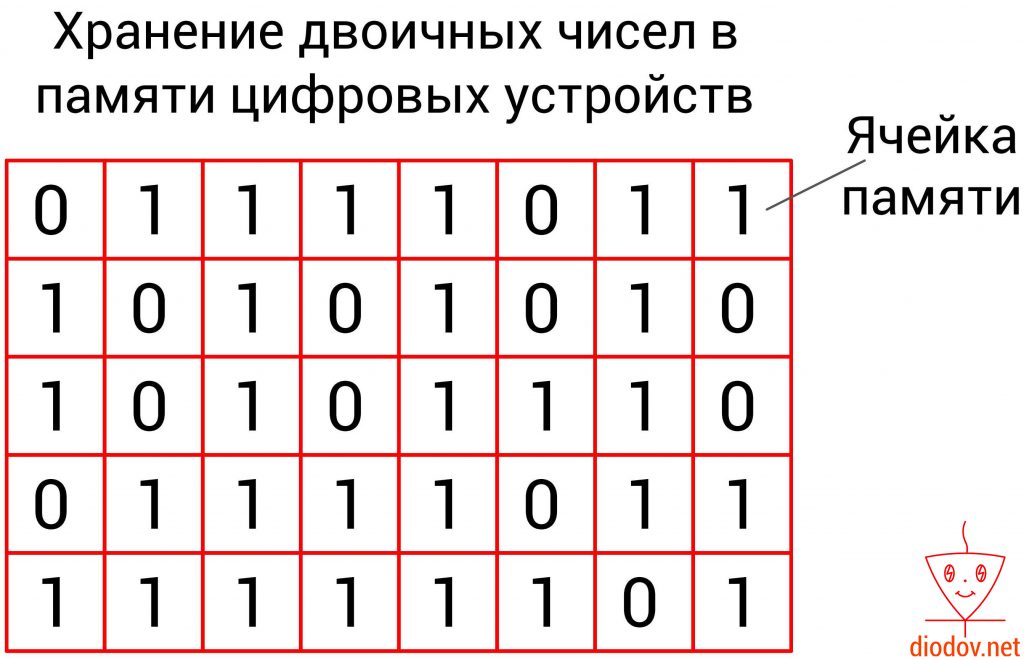
Вся информация цифровых запоминающих устройств хранится в памяти. Память представляет собой набор ячеек.

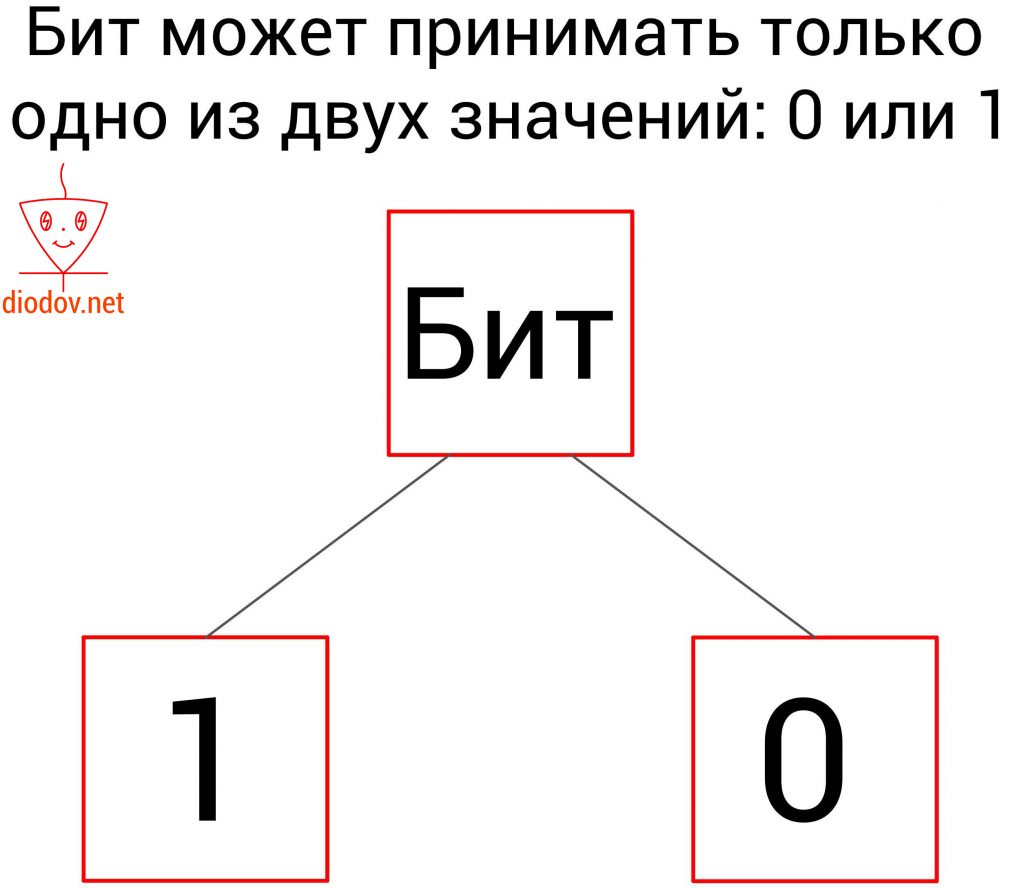
Каждая ячейка содержит один бит данных. Бит – это единица измерения объема памяти. В одном бите можно запоминать максимум два значения: 0 – это одно значение, а 1 – второе.

Bit происходит от двух английских слов Binary Digit (двоичное число).

При работе с битами регистров микроконтроллера мы будем часто обращаться к таким понятиям, как старший и младший биты. Эти понятия строго регламентированы. В двоичной системе разряд, который имеет самую правую позицию, получил название младший значащий бит (МЗБ). В англоязычной литературе его называют Least Significant Bit (LSB). Именно с него начинается нумерация битов.

Наибольший вес имеет бит, находящийся в самой левой ячейке памяти. Его принято называть старший значащий бит (СЗБ) или Most Significant Bit – MSB.

Более емкой единицей информации является байт (byte). Он равен 8 битам, т. е. восемь элементарных ячеек памяти составляют один байт.

1 байт = 8 бит

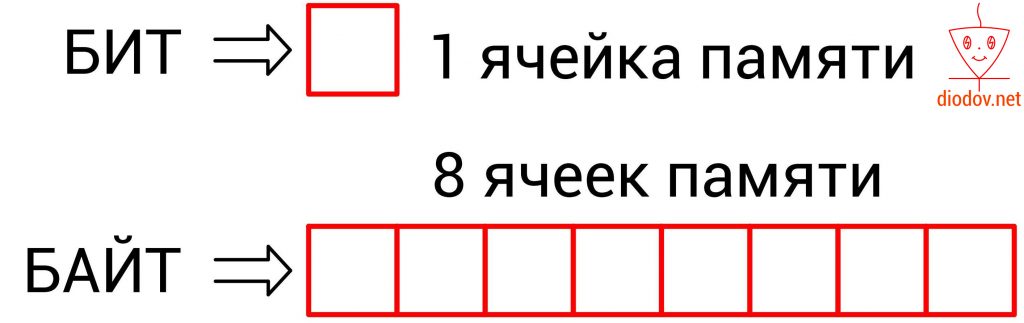
В одном бите можно хранить только два разных значения или две комбинации. А в 1 байте можно хранить 256 различных комбинаций. Ровно столько же символов содержится в таблице кодировки ASCII. Но об этом в другой раз.

На практике пользуются большими значениями объёма памяти килобайтами, мегабайтами, гигабайтами и терабайтами.

1 килобайт (кБ) = 1024 байт

1 мегабайт (МБ) = 1024 кБ

1 гигабайт (ГБ) = 1024 МБ

1 терабайт (ТБ) = 1024 ГБ

Преобразование десятичного числа в двоичное

На практике программисты часто пользуются несколькими системами счисления. Поэтому следует научиться переводить числа из десятичной системы в двоичную. Здесь можно выделить два простых способа. Рассмотрим их по порядку.

Первый способ заключается в том, что десятичное число непрерывно делится на два. При этом учитывается полностью ли оно разделилось или с остатком. Если значение делится без остатка, как например 4/2 = ровно 2 или 6/2 = ровно 3, то записывается ноль, а если с остатком, как 3/2 или 5/2, то записывается единица.

Теперь давайте переведем число 125 в двоичную форму.

125/2 = 62 остаток 1

62/2 = 31 остаток 0

31/2 = 15 остаток 1

15/2 = 7 остаток 1

7/2 = 3 остаток 1

3/2 = 1 остаток 1

1/2 = 0 остаток 1

Получаем двоичное число 1111101₂

Я надеюсь здесь понятно, что если 1 разделить на 2, то математически ноль никак не получится, однако такой подход позволяет объяснить данный алгоритм.

Еще один пример.

84/2 = 42 остаток 0

42/2 = 21 остаток 0

21/2 = 10 остаток 1

10/2 = 5 остаток 0

5/2 = 2 остаток 1

2/2 = 1 остаток 0

1/2 = 0 остаток 1

Второй способ

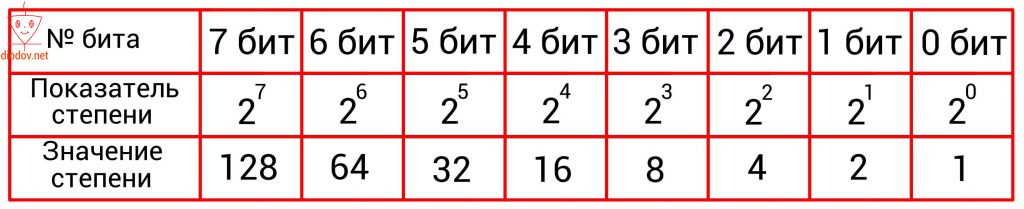
Второй способ имеет такую идею. С изначального числа нужно вычесть число в степени два, которое будет меньше заданного значения. Для ускорения процесса преобразования воспользуемся следующей таблицей.

Давайте преобразуем 125.

Наибольшая степень числа 2 меньшая значения 125 равна 6, т.е. 2 6 . Два в шестой степени равно 64. В 6-й бит записываем единицу. Теперь от 125 отнимаем 64 и получаем 61. Ближайшая степень двойки является 5, т. е. число 32. Следовательно, 5-й бит также находится в единице. Отнимаем от 61 значение 32 и получаем 29. 4-й бит, который соответствует числу 16, также находится в единице. 29 – 16 = 13, поэтому и 3-й бит = 1. 13 – 8 = 5. Отсюда видно, что и второй бит находится в единице. Далее от 5 отнимаем 4 и получаем единицу. Поскольку 1-й бит равен двум (2 1 = 2), а два менее единицы, то в него записываем ноль. Нулевой бит равен одному (2 0 = 1), поэтому в него заносим единицу. В итоге получаем следующее двоичное число: 1111101₂.

Следует обратить особое внимание на то, что нумерация битов, во-первых, выполняется справа налево, а во-вторых начинается с нуля! Это несколько непривычно, поскольку в десятичной системе счисления счет принято начинать с единицы. Однако в цифровой технике счет всегда идет с нуля! К этому следует приучить себя заранее, так как при написании программ для микроконтроллеров мы все время будем начинать счет битов с нуля. В дальнейшем вы такому счету быстро привыкнете, поскольку и в техническом описании МК строго соблюдается данное правило.

Преобразование двоичного числа в десятичное

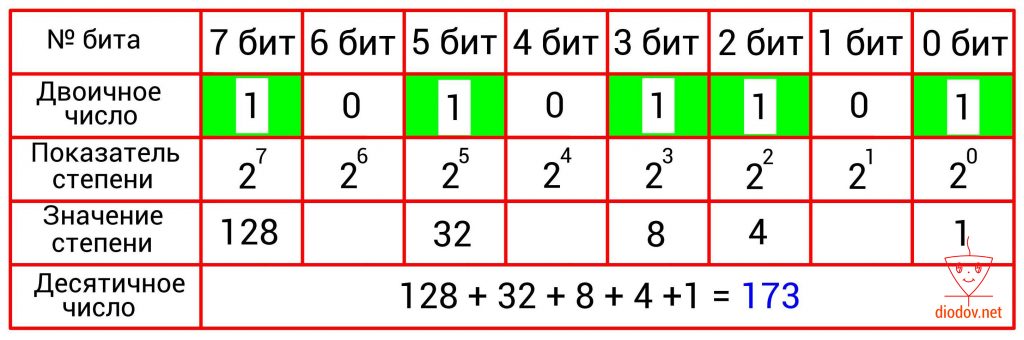
Преобразование двоичного числа в десятичное выполняется довольно просто. Для этого следует сложить десятичные веса всех двоичных разрядов, в которых имеются единицы. Биты, в которых записан ноль, пропускаются. В качестве примера возьмем такое значение: 10101101. Нулевой, второй, третий, пятый и седьмой биты имеют единицы. Получаем: 2 0 + 2 2 + 2 3 + 2 5 + 2 7 = 1 + 4 +8 + 32 + 128 = 173.

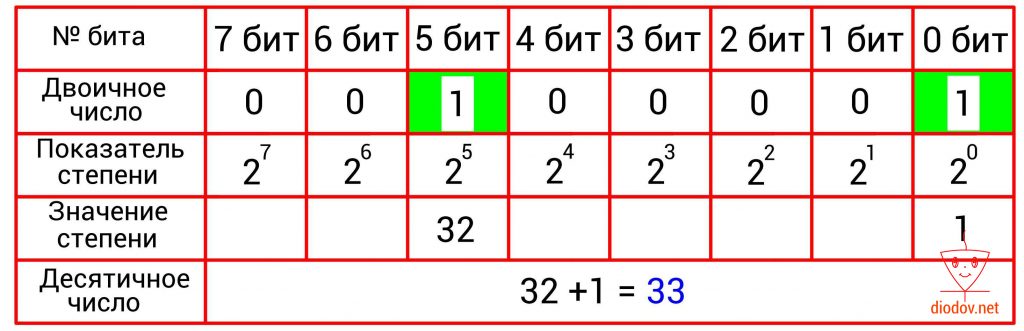
В таблицах, приведенных ниже, наглядно показано перевод чисел из двоичной в десятичную систему счисления.

Шестнадцатеричная система счисления

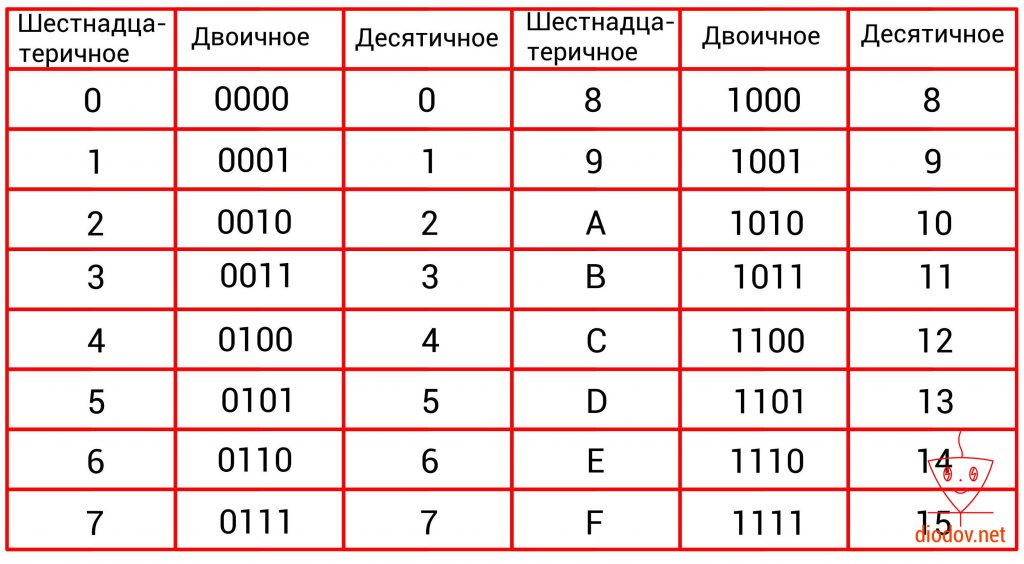
В программировании микроконтроллеров очень часто пользуются шестнадцатеричными числами. Данная система счисления имеет основание 16, соответственно и 16 различных символов. Первые десять символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 заимствованы из десятеричной системы. В качестве оставшихся шести символов применяются буквы A, B, C, D, E, F.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Высокая популярность шестнадцатеричной системы счисления поясняется тем, что при отображении одного и того же значения используется меньше разрядов по сравнению с десятичной системой и тем более с двоичной. Например, при отображении 100 используется три десятичных разряда 100₁₀ или 7 двоичных разрядов 1100100₂ и только 2 шестнадцатеричных разряда 64₁₆.

А если записать 1000000, то разница в количестве занимаемых разрядов буде еще более ощутима:

1 000 000₁₀ = 1111 0100 0010 0100 0000₂ = F4240₁₆

Преобразование двоичного числа в шестнадцатеричное

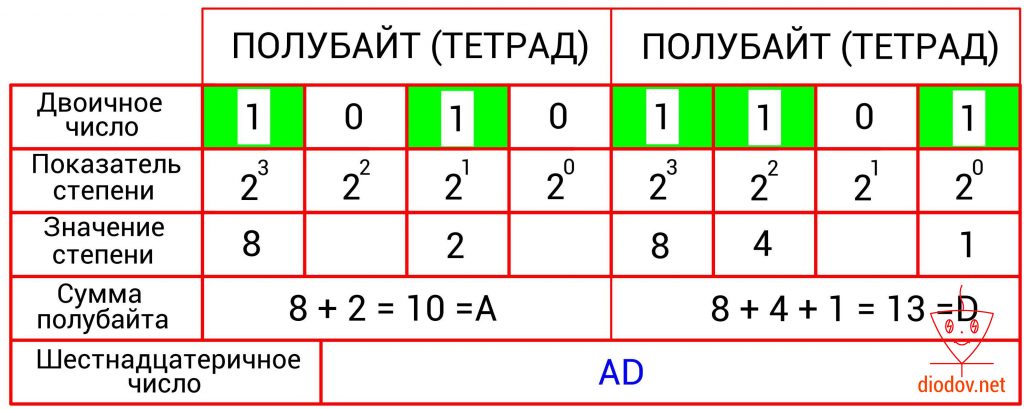
Еще одним положительным свойством шестнадцатеричного числа является простота получение его из двоичного. Такое преобразование выполняется следующим образом: сначала двоичное число разбивается на группы по четыре быта или на полубайты, которые еще называют тетрадами. Если количество битов не кратно четырем, то их дополняют нулями. Далее следует сложить значение всех битов в каждом полубайте. Сумма каждого полубайта даст значение отдельной цифры шестнадцатеричного числа.

Другие системы счисления

В цифровой технике также применяется восьмеричная система счисления, но она не нашла применения в микроконтроллерах.

Теоретические можно получить бесконечное значение систем счисления: троичную, пятиричную и даже сторичную, т.е. с любым основанием. Однако практической необходимости в этом пока что нет.

Наиболее простой и быстрый способ преобразования чисел с одной системы счисления в другую – это применение встроенного в операционную систему калькулятора. Найти его можно следующим образом: Пуск – Все программы – Стандартные – Калькулятор.

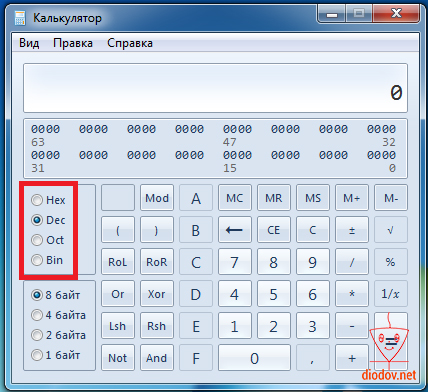
Чтобы перейти в «нужный» режим следует кликнуть по вкладке Вид и выбрать Программист или нажать комбинацию клавиш Alt+3.

В открывшемся окне можно вводить двоичные, восьмеричные, шестнадцатеричные и десятичные числа, выбрав соответствующий режим. Кроме того можно выполнять различные математические операции между ними.

В дальнейшем, при написании кода программы мы часто будем обращаться к данному калькулятору. Кроме того, опытные программисты любят использовать шестнадцатеричные числа, а нам проще будет понять двоичный код, поэтому калькулятор в помощь)

Источник