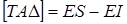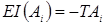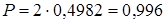Расчет размерной цепи вероятностным методом
Назначение предельных отклонений составляющих звеньев размерной цепи при известном допуске замыкающего звена называется прямой задачей, которая может быть решена либо методом полной взаимозаменяемости, либо методом вероятностного расчёта. В данной курсовой работе производим расчет размерной цепи вероятностным методом, что позволяет установить на составляющие звенья более широкие допуски, чем те, которые получаются при решении задачи методом полной взаимозаменяемости. В основе этого метода служат теоремы математической статистики, устанавливающие свойства дисперсии. Замыкающее звено размерной цепи принимается за случайную величину, являющуюся суммой независимых случайных переменных, т.е. суммой независимых составляющих звеньев цепи. Как известно из теории вероятности, при любых законах распределения случайных погрешностей отдельных составляющих звеньев погрешность замыкающего звена также будет случайной погрешностью, подчиняющейся определённому закону распределения.
Распределение размеров в пределах допуска может происходить по одному из следующих законов:
а) нормального распределения;
б) равнобедренного треугольника (Симпсона);
в) равной вероятности.
| А1 | А2 | А3 | А4 | А5 | А6 | А  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | 120 | 40 | 100 | 70 | 400 |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| РВ | РТ | Н | РТ | РТ | Н | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— коэффициент относительного рассеивания, который равен для:
. Возводим это произведение в квадрат, где 
— единица допуска, которая выбирается в зависимости от номинальных размеров по ГОСТ 23347 – 82.| А1 | А2 | А3 | А4 | А5 | А6 |
| 70 | 120 | 40 | 100 | 70 | 400 |
| 1,86 | 2,17 | 1,56 | 2,17 | 1,86 | 3,54 |
9.4.1 Суммируем все значения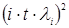 
и определяем значение среднего коэффициента точности цепи – аср по формуле:
аср= 
(9.2),
где [TA 
] – замыкающее значение допуска, мкм
мм = 1600 мкм
Таблица 8 – Расчет средней точности размерной цепи.
| Аi ном | i | t | λi | (i·t·λi) 2 |
| 70 | 1,86 | 3,00 | 0,577 | 10,37 |
| 120 | 2,17 | 3,00 | 0,408 | 7,06 |
| 40 | 1,56 | 3,00 | 0,333 | 2,43 |
| 100 | 2,17 | 1,96 | 0,408 | 3,01 |
| 70 | 1,86 | 3,00 | 0,408 | 2,28 |
| 400 | 3,54 | 3,00 | 0,333 | 3,54 |
аср= = 
мкм
По полученному значению аср из табл.1.2[4] выбираем ближайший более точный квалитет допусков звеньев размерной цепи.
Принимаем а = 250, что соответствует 13 квалитету.
9.5 Определение вероятностного допуска замыкающего звена.
По табл.1.3[4] (ГОСТ 25347 – 82) определяем допуски составляющих звеньев размерной цепи.
Таблица 9 – Расчет вероятностного допуска замыкающего звена
| Аi ном | TAi | λi | t | (TAi · λi·t) 2 |
| 70 | 460 | 0,577 | 3,00 | 634029,99 |
| 120 | 540 | 0,408 | 3,00 | 436868,12 |
| 40 | 390 | 0,333 | 3,00 | 151795,95 |
| 100 | 540 | 0,408 | 1,96 | 186474,73 |
| 70 | 460 | 0,408 | 3,00 | 317014,04 |
| 400 | 890 | 0,333 | 3,00 | 790516,59 |
9.6 Рассчитываем вероятностный допуск замыкающего звена по формуле:
(9.3)
мкм
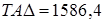
Условие TA 
[TA 
] выполняется.
1586,4 
1600
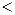
9.7 Полученные допуски составляющих звеньев разбиваем на отклонения, пользуясь следующими правилами:
а) если среднее отклонение звена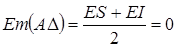 
, то отклонение для всех звеньев принимаются симметрично, т.е. 
;
б) если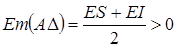 
то отклонения принимаются
— для увеличивающихся звеньев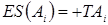 
; 
— для уменьшающихся звеньев 
; 
в) если 
, то отклонения принимаются
— для увеличивающихся звеньев 
; 
— для уменьшающихся звеньев ;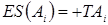 
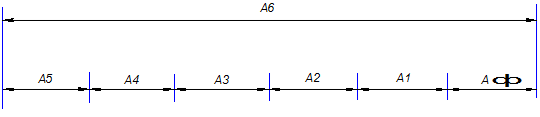
Звено А6 – увеличивающееся
Звенья А1-А5 – уменьшающиеся
мм = 0 мкм, то отклонения:
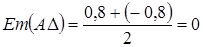
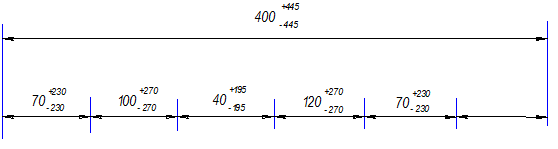
А1: ES(70) = +230 мкм EI(70) = -230 мкм
А2: ES(120) = +270 мкм EI(120) = -270 мкм
А3: ES(40) = +195 мкм EI(40) = -195 мкм
A4: ES(100) = +270 мкм EI(100) = -270 мкм
A5: ES(70) = +230 мкм EI(70) = -230 мкм
A6: ES(400) = +445 мкм EI(400) = -445 мкм
Так как разбивка отклонений произвольна, то обязательное условие 
может не выполняться.
мкм
– условие выполняется
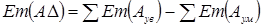
9.8 Процент годных деталей при сборке размерной цепи вычисляют в следующей последовательности:
а) Определяем средне квадратичное отклонение звена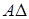 
:
(9.4),
Где [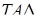 
] – заданное значение допуска, мкм:
мкм
б) Находим границы нового допуска:
Х=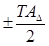 
(9.7),
где 
— вероятный допуск, мкм
Х= 
мкм
в) Находим пределы интегрирования расчетного вероятностного допуска Z:
(9.8)
Г) Рассчитываем вероятность изготовления годных деталей по формуле:
(9.9),
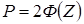
Где Ф(Z) – значение функции Лапласа
Ф(2,97) = 0,4982; 
д) Процент годных деталей:
(9.10)
(9.11)
Список используемой литературы
1. Расчет посадок с зазорами и натягами. Допуски и посадки подшипников качения. Выбор средств измерения. Допуски зубчатых передач: Произв. – техн. Материалы к учеб. Занятиям по курсу «Взаимозаменяемость, стандартизация и технические измерения»: для студентов спец. 170500, 170600/Воронеж. Гос. Технол. Акад.; Сост. А.А. Афанасьев, В.И. Логинова, Ю.М. Веневцев, И.М. Комарчев. Воронеж, 1997. 40 с.
2. Курсовое проектирование деталей машин: Учеб. Пособие для учащихся машиностроительных специальностей техникумов/С.А. Чернавский, К.Н. Боков, И.М. Чернин и др. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1988. – 416 с.: ил.
3. Допуски и посадки: Справочник: В 2-х ч./В.Д. Мягков, М.А. Палей, А.Б. Романов, В.А. Брагинский. – 6-е изд. П.: Машиностроение, 1982. – Ч.1,1983. – Ч. 2.
4. Афанасьев А.А., Веневцев Ю.М. Допуски отверстий, валов, резьб, калибров: учебное пособие ВГТА/А.А. Афанасьев, Ю.М. Веневцев. Воронеж, 1994. – 44 с.
5. Методические указания к оформлению расчетно-проектных, расчетно-графических работ, курсовых и дипломных проектов/Воронеж. Гос. Технол. Акад.; Сост. Ю.Н. Шаповалов, В.Г. Савенков, Е.В. Вьюшина. Воронеж, 1998. – 50 с.
6. Взаимозаменяемость, стандартизация и технические измерения: Учебник для вузов/А.И Якушев, Л.Н. Воронцов, Н.М. Федотов. – 6-е изд., перераб. и доп. – М.: Машиностроение, 1986. – 352 с.
7. Справочник контролера машиностроительного завода. Допуски, посадки, линейные измерения/А.Н. Виноградов, Ю.А. Воробьев, Л.Н. Воронцов и др.; под ред. А.И. Якушева. – 3-е изд. – М.: Машиностроение, 1980. – 367 с.
Источник
