Определители 2-го и 3-го порядков
Рассмотрим квадратную матрицу 2-го порядка:
Определение. Определителем 2-го порядка, соответствующим матрице А, называется число
.
Числа а11, а12, а21, а22 называются элементами определителя (они же элементы матрицы А).
Элементы а11, а22 составляют главную диагональ, а элементы а21, а12 – побочную диагональ.
Пусть дана квадратная матрица 3-го порядка:
.
Определение. Определителем 3-го порядка, соответствующим матрице А, называется число D, которое определяется выражением:
Элементы а11, а22, а33 – расположены на главной диагонали, элементы а13, а22, а31 – на побочной диагонали.
Вычисление определителей 2-го и 3-го порядка
Определитель 2-го порядка вычисляется по определению:
.
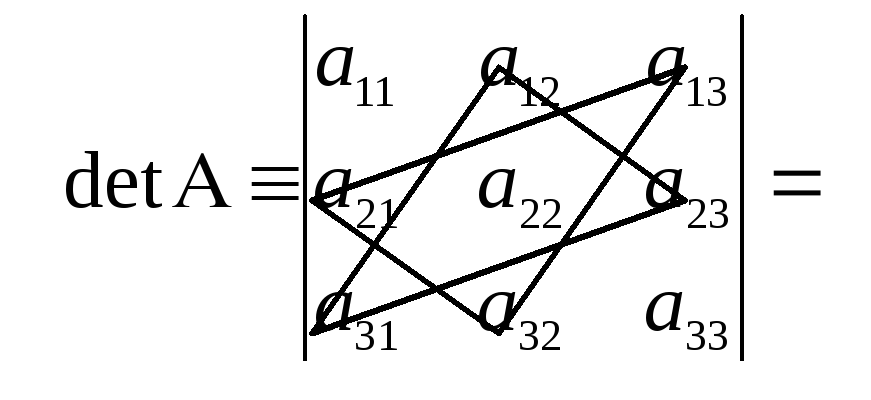
Для вычисления определителя 3-го порядка можно воспользоваться следующими правилами:
Правило Саррюса: дописать справа к элементам определителя сначала 1-й столбец, затем 2-й (можно внизу дописать первую и вторую строки), (рис.1), произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «плюс», а произведение элементов побочной диагонали и двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «минус» (рис. 1). Сумма этих шести произведений дает определитель 3-го порядка, соответствующий матрице А.
,
Вычислить 
.
,
Правило треугольника:одно из трех слагаемых, со знаком «плюс» есть произведение элементов главной диагонали определителя, каждое из двух других – произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла определителя, слагаемые со знаком «минус» строятся так же, но относительно побочной диагонали (рис.2).
Пример 3
Вычислить определитель по правилу треугольника: 
.
Решение
Свойства определителей
Рассмотрим свойства определителей на примере определителя 3-го порядка.
.
Определение. Минором некоторого элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, на пересечении которых стоит этот элемент. Обозначение минора 
.
Пример 4
Минор элемента а12: 
.
Определение. Алгебраическим дополнениемлюбого элемента определителя называется минор этого элемента, взятый со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит этот элемент, есть число четное, либо с противоположным знаком, если эта сумма есть число нечетное. Обозначение алгебраического дополнения Аij.
Пример 5
Свойство 1.Определитель равен сумме произведений элементов какого-нибудь столбца (или строки) на их алгебраические дополнения.
Пример 6
Вычислим определитель, разложив его по элементам 1-ой строки:
.
Свойство 2. Величина определителя не изменится, если каждую его строку заменить столбцом с тем же номером.
Свойство 3. Перестановка двух столбцов или двух строк определителя равносильна его умножению на (–1).
Свойство 4.Общий множитель всех элементов одного столбца или одной строки определителя можно вынести за знак определителя.
Свойство 5. Если все элементы какой-либо строки или какого-либо столбца равны нулю, то определитель равен нулю.
Свойство 6. Определитель, имеющий два одинаковых столбца или две одинаковых строки, равен нулю.
Свойство 7. Определитель равен нулю, если элементы двух столбцов или двух строк пропорциональны.
Свойство 8. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые слагаемые, а во втором – вторые:
.
Свойство 9.Если к элементам некоторого столбца (или строки) определителя прибавить соответствующие элементы другого столбца (или строки), умноженные на общий множитель, то величина определителя не изменится.
Пример 7
,
при вычислении определителя первую строку умножили на 2 и сложили со второй, затем разложили определитель по 2-й строке.
Свойство 10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или строки) определителя равна нулю.
Обратная матрица
Пусть дана квадратная матрица А порядка n.
Обратной матрицей по отношению к данной А называется матрица 
, которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
А · 
= · А = Е.
Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной.
Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
,
где 
— определитель матрицы А, 
— союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
,
для квадратной матрицы 3-го порядка союзной является матрица
.
Пример
Для матрицы 
найти обратную.
Обратную матрицу находим по формуле
.
Определитель матрицы 
, следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
.
Тогда обратная матрица имеет вид
.
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.
ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник
1.2. Определители второго, третьего, n-го порядка
Звуковое сопровождение лекции
Рассмотрим квадратную матрицу 2-го порядка
.
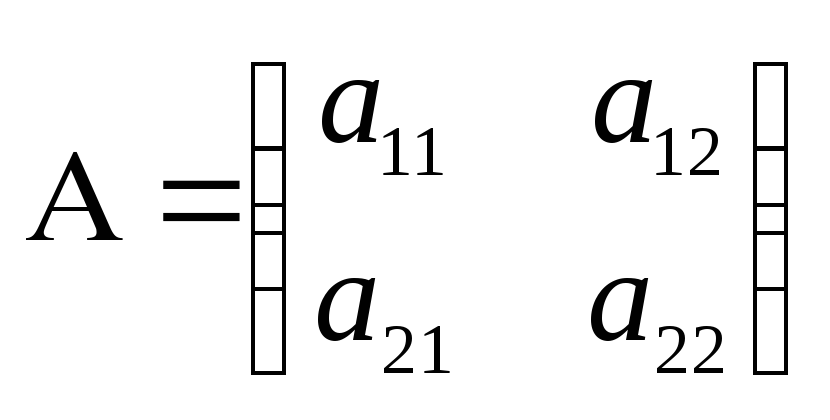
Определителем второго порядка, соответствующим квадратной матрице второго порядка, называется число, обозначаемое 
или 
, равное
.
Определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов на побочной диагонали.
.
Пример 1(для самопроверки)
Вычислите определитель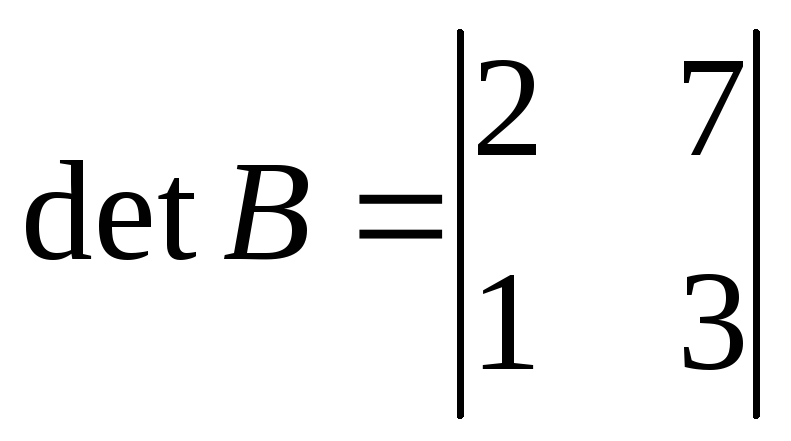 
.
Рассмотрим квадратную матрицу третьего порядка
.
Определителем третьего порядка, соответствующим квадратной матрице третьего порядка, называется число
.
В выражение определителя со знаком ‘’ входят произведение элементов, стоящих на главной диагонали, и произведения элементов, расположенных в вершинах треугольников, основания которых параллельны главной диагонали; со знаком ‘’ . (то же про побочную диагональ).
.
Пример 2(для самопроверки)
Вычислите определитель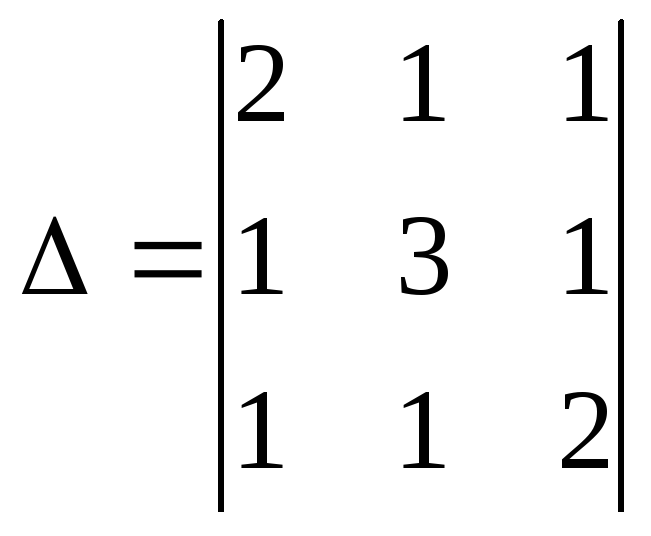 
.
Пример 3(для самопроверки)
Вычислите определитель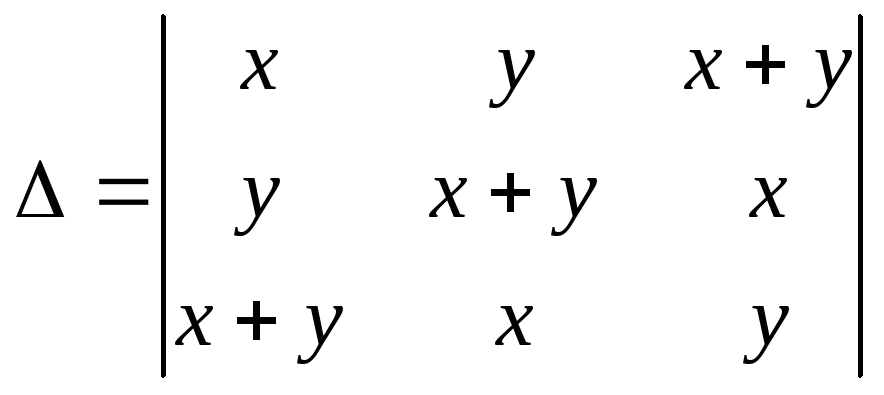 
.
Определителем 
-го порядка, соответствующим матрице 
-го порядка, называется число, равное сумме всевозможных произведений элементов матрицы, взятых по одному из каждой строки и из каждого столбца и снабженных знаками «+» или «–» по некоторому определенному правилу (строгое определение этого понятия можно найти в учебной литературе, в данном курсе оно не требуется).
1.3. Свойства определителей
(уметь доказывать для определителей третьего порядка)
Звуковое сопровождение лекции
1. При транспонировании матрицы ее определитель не меняется:
.
Вычислить левую и правую части равенства по правилу треугольника и сравнить результаты.
2. Перестановка любых двух строк (столбцов) меняет знак определителя:
.
3. Определитель с двумя равными строками (столбцами) равен нулю:
.
Рассмотрим 
. Переставим в этом определителе первую и вторую строки. По предыдущему свойству
.
Следовательно, 
. Отсюда
.
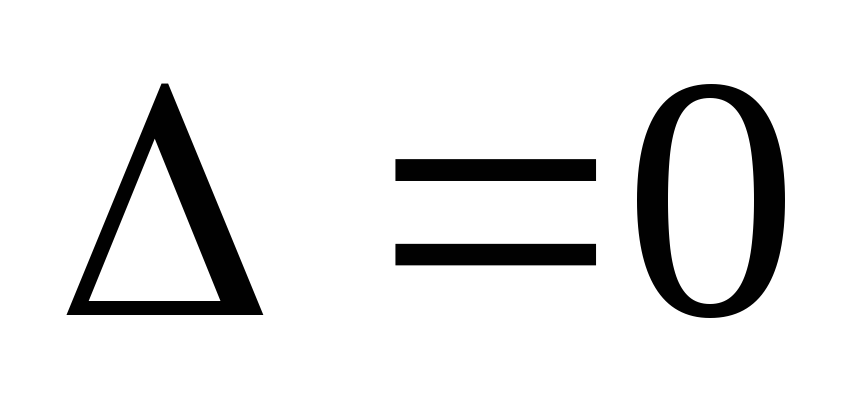
4. Общий множитель строки (столбца) можно выносить за знак определителя:
.
5. Определитель, у которого две строки (2 столбца) пропорциональны, равен нулю:
.
6. Определитель, в некоторой строке которого каждый элемент равен сумме двух слагаемых, равен сумме двух определителей:
.
7. Величина определителя не изменится, если ко всем элементам некоторой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число 
:
.
В новом определителе без изменения записывается строка, которую умножали на 
(рабочая строка).
1.4. Разложение определителя по элементам строки или столбца
Звуковое сопровождение лекции
Минором 
элемента квадратной матрицы 
называется определитель, полученный из данного путем вычеркивания
-й строки и
-го столбца.
, 
.
Алгебраическим дополнением 
элемента квадратной матрицы 
называется число
.
.
.
Пример 4(для самопроверки)
Для определителя 
найдите миноры и алгебраические дополнения элементов 
и 
.
8. Величина определителя равна сумме произведений элементов некоторой строки (столбца) на их алгебраические дополнения:
–
– формула разложения определителя третьего порядка по первой строке.
Для определителя 
-го порядка:
–формула разложения по элементам 
-го столбца;
–формула разложения по элементам 
-й строки.
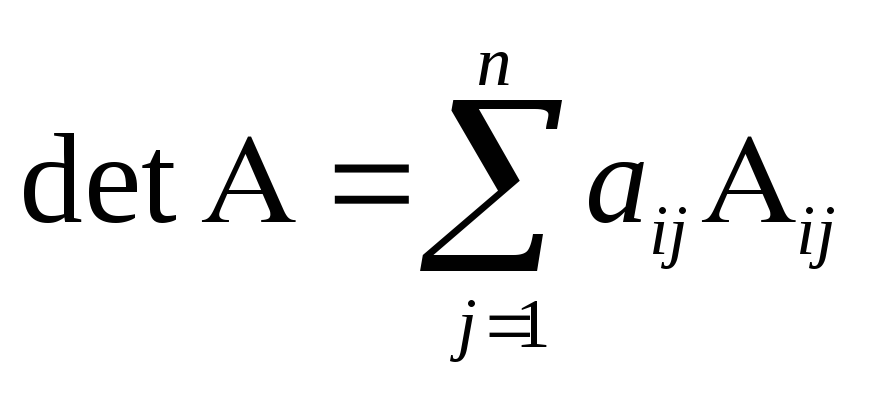
В формулах разложения 
выражается через определители порядка
, т.е. на единицу меньше исходного.
9. Сумма произведений элементов некоторой строки (столбца) на соответствующие алгебраические дополнения элементов другой строки (столбца) равна нулю:
.
10. Величина определителя треугольной матрицы равна произведению элементов, стоящих на главной диагонали:
.
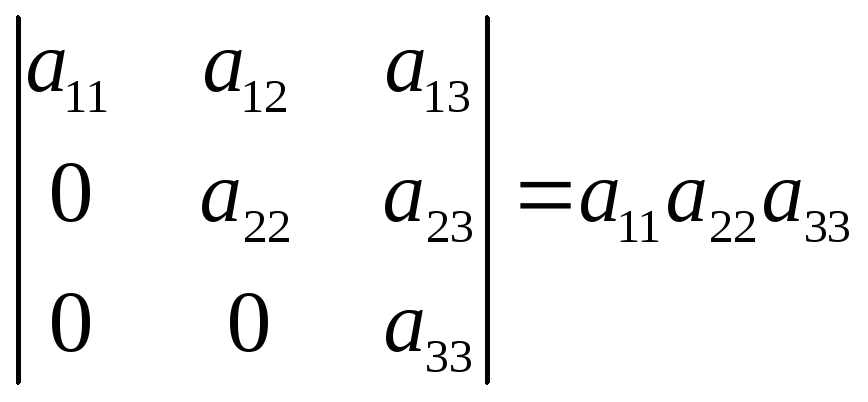
Разложим определитель по элементам первого столбца:
.
Перечисленные свойства используются при вычислении определителей.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
