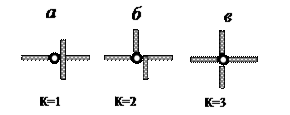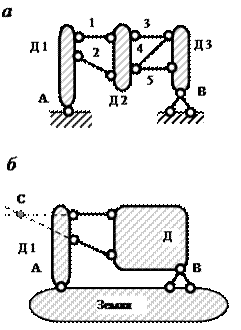
2 геометрические способы образования неизменяемых систем порядок кинематического анализа сооружений

Источник

Лекция 2 КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ. Внешняя нагрузка может вызвать значительные перемещения элементов сооружения, в результате чего оно может перестать. — презентация

Презентация была опубликована 6 лет назад пользователемАнна Талалыкина

Похожие презентации

Презентация на тему: » Лекция 2 КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ. Внешняя нагрузка может вызвать значительные перемещения элементов сооружения, в результате чего оно может перестать.» — Транскрипт:

1 Лекция 2 КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ

2 Внешняя нагрузка может вызвать значительные перемещения элементов сооружения, в результате чего оно может перестать служить своему предназначению. Поэтому ставится требование: «перемещения сооружения должны быть малыми». Решением этой задачи на начальном этапе проектирования занимается специальный раздел строительной механики – кинематический анализ. Кинематический анализ – это анализ геометрической структуры сооружения с целью исключения больших перемещений. При кинематическом анализе внешняя нагрузка не рассматривается, а элементы системы считаются достаточно жесткими. Кинематический анализ рассматривает три типа расчетных схем: 1) неизменяемые, 2) изменяемые, 3) мгновенно изменяемые системы.

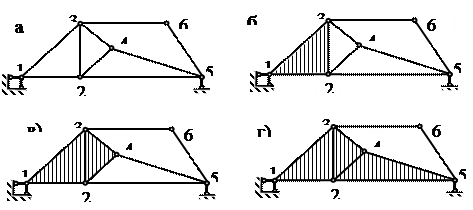
3 Геометрически неизменяемая система (ГНС) – это система, перемещения которой возможны только при деформации его элементов. Простейшая ГНС шарнирный треугольник (рис а). Геометрически изменяемая система (ГИС) – это система, элементы которой могут получать перемещения даже без их деформаций. Например, ГИС является шарнирный четырехугольник (рис. б). Мгновенно изменяемая система (МИС) – система, способная получать лишь мгновенные перемещения (рис. в).

4 1. Степень свободы. Кинематические связи Количественная оценка кинематических свойств системы основана на понятии степени свободы как направления возможного независимого перемещения. Число степеней свободы (W) – это минимальное число независимых параметров, необходимых для определения положения всех точек системы. Такими параметрами могут быть перемещения отдельных точек, углы поворота элементов и др. Число степеней свободы простых систем можно определять путем задания ее элементам возможных перемещений (рис. а, б, в):

5 Для изучения более сложных случаев введем понятия: диск (Д) – неизменяемая часть системы, состоящая из одного или нескольких жестко связанных элементов (рис. а); шарнир (Ш) – связь, дающая возможность взаимного поворота соседним дискам (рис. б); припайка (П) – связь, жестко закрепляющая соседние диски (рис. в); стержень (С) – связь, ограничивающая перемещение диска в одном направлении (рис. г); опорная связь (С 0 ) – связь, ограничивающая перемещение диска в одном направлении по отношению к земле (рис. д).

6 Определим число степеней свободы точки (рис. а) и диска с различными кинематическими связями (рис. б-д): Следовательно, стержень или опорная связь уменьшают число степеней свободы на единицу, шарниры – на два, припайки – на три. Кинематические связи должны обеспечивать неподвижность системы относительно земли (основания), а также неизменяемость ее внутренней структуры. Если при удалении одной связи из неизменяемой системы она становится изменяемой, то эта связь называется необходимой. Если после этого система остается неизменяемой, то связь называется избыточной. Связь, соединяющая систему с землей, называется внешней, а находящаяся внутри – внутренней связью.

7 Шарнир, объединяющий два диска называется простым шарниром (рис. а). Если шарнир объединяет несколько дисков, то он называется кратным шарниром. Кратный шарнир эквивалентен нескольким простым шарнирам. Кратность шарнира определяется по формуле n Ш =n Д –1. Здесь n Д – число дисков, объединяемых шарниром.

8 Рассматривая расчетную схему сооружения как систему дисков объединенных связями, получаем ее дисковый аналог. 2. Число степеней свободы стержневой системы

9 Число степеней свободы плоской стержневой системы определяется по основной формулой кинематического анализа: W = 3n Д – 2n Ш – n C – – 3n П, где n Д – число дисков в дисковом аналоге n Ш – число простых шарниров n С – число стержней – число опорных связей; n П – число припаек. Например, для арки имеем: W=3 2 – 2 1 – 0 – 4 –3 0 =0. При расчете ферм можно использовать формулу W = 2n У – n C –, где n У – число узлов фермы (узлом считается любой шарнир, связывающий стержни фермы). Для фермы имеем: W = 2 4 – 5 – 3 = 0.

0 – такая система ГИС, т.е. геометрически изменяема; 2) W=0 – в системе имеется достаточное число связей; если эти связи введены правильно, система неизменяема и статически определима; 3) W» title=»После расчета по этим формулам возможны три случая: 1) W>0 – такая система ГИС, т.е. геометрически изменяема; 2) W=0 – в системе имеется достаточное число связей; если эти связи введены правильно, система неизменяема и статически определима; 3) W» > 10 После расчета по этим формулам возможны три случая: 1) W>0 – такая система ГИС, т.е. геометрически изменяема; 2) W=0 – в системе имеется достаточное число связей; если эти связи введены правильно, система неизменяема и статически определима; 3) W 0 – такая система ГИС, т.е. геометрически изменяема; 2) W=0 – в системе имеется достаточное число связей; если эти связи введены правильно, система неизменяема и статически определима; 3) W»> 0 – такая система ГИС, т.е. геометрически изменяема; 2) W=0 – в системе имеется достаточное число связей; если эти связи введены правильно, система неизменяема и статически определима; 3) W»> 0 – такая система ГИС, т.е. геометрически изменяема; 2) W=0 – в системе имеется достаточное число связей; если эти связи введены правильно, система неизменяема и статически определима; 3) W» title=»После расчета по этим формулам возможны три случая: 1) W>0 – такая система ГИС, т.е. геометрически изменяема; 2) W=0 – в системе имеется достаточное число связей; если эти связи введены правильно, система неизменяема и статически определима; 3) W»>

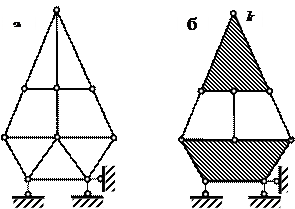
11 3. Способы образования неизменяемых систем Выполнение условия W 0 необходимо, но не достаточно. Например, у систем на рис. а, б W=0, но первая из них ГИС, а другая ГНС. Причиной изменяемости системы а) является неправильная установка связей. Чтобы она стала неизменяемой, одну связь нужно переставить (рис. б). То же самое имеет место и для систем на рис. б и г.

12 Из этих примеров следует, что для полной уверенности в неизменяемости системы нужна дополнительная проверка – проверка геометрической структуры. Ее суть заключается в проверке способов объединения элементов между собой и с землей. Для такой проверки необходимо: – выделить в системе неизменяемые фигуры – диски; – последовательно объединять эти диски между собой, используя способы образования неизменяемых систем.

13 Простейшие способы образования неизменяемых систем: 1. Новый узел к диску добавляется способом диады (рис. а). 2. Два диска объединяются: – одним шарниром и одной связью (рис. б); – способом триады (рис. в). 3. Три диска объединяются тремя шарнирами, не лежащими на одной прямой (рис. г). Шарниры могут быть условными (рис. д).

14 4. Понятие о мгновенно изменяемых системах Мгновенная изменяемость часто возникает при неправильной установке связей (рис. а, г, д, е). Обнаружить мгновенную изменяемость очень важно уже на этапе кинематического анализа, так как позволяет вносить коррективы в расчетную схему сооружения.

15 Для этого можно использовать метод нулевой нагрузки. Суть этого метода: – удалить все силы, действующие на систему; – вычислить внутренние усилия. Если они все (включая и опорные реакции) будут равны нулю, то система неизменяема. Если же хотя бы одно усилие будет неопределенным (типа 0/0), то данная система является мгновенно изменяемой. Общие выводы Расчетная схема сооружения должна быть геометрически неизменяемой. С целью проверки геометрической неизменяемости проводится кинематический анализ, состоящий из двух этапов: 1) количественный анализ – проводится по основной формуле кинематического анализа; должно выполняться условие W 0; 2) качественный анализ – проводится с использованием принципов образования геометрически неизменяемых систем.

16 В о п р о с ы 1. Какие системы называются геометрически не изменяемыми, изменяемыми и мгновенно изменяемыми? 2. Что такое число степеней свободы? 3. Как пишется основная формула кинематического анализа? 4. Как классифицируются системы по степени свободы? 5. В чем заключается необходимое условие геометрической неизменяемости системы? 6. Как проверяется геометрическая структура системы? 7. Какие способы образования неизменяемых систем знаете? 8. Каков порядок кинематического анализа? 9. Что такое метод нулевой нагрузки?

Источник

2 геометрические способы образования неизменяемых систем порядок кинематического анализа сооружений

3. Примеры кинематического анализа

3.1. Правила образования геометрически неизменяемых систем

Любую геометрически неизменяемую часть системы назовем диском.

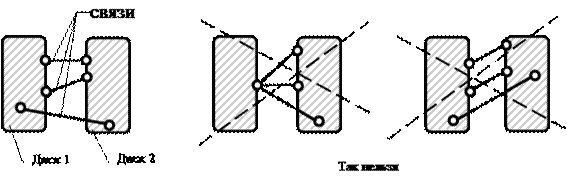
П равило 1: узел присоединяется к диску двумя связями, не лежащими на одной прямой (рис. 3.1).

Правило 2: диск соединяется с другим диском тремя связями, не пересекающимися в одной точке и не параллельными друг другу (рис. 3.2).

Точка пересечения двух связей может рассматриваться как шарнир – действительный или фиктивный. Поэтому правило 2 можно трактовать как соединение двух дисков с помощью шарнира и одной связи, не проходящей через шарнир. Например, два диска, показанные на рис. 3.3, соединены действительным шарниром А и связью 3. Можно также считать, что диски соединены фиктивным шарниром В и связью 1.

Рис.3.1. Присоединение узла к диску

Рис.3.2. Соединение двух дисков тремя связями

Рис.3.3. Соединение двух дисков шарниром и стержнем:

А – действительный шарнир; В – фиктивный шарнир

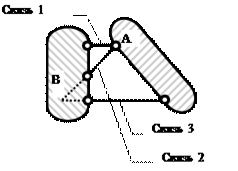
Правило 3: три диска соединяются друг с другом тремя шарнирами, не лежащими на одной прямой (рис. 3.4). Шарниры могут быть действительными или фиктивными.

Рис.3.4. Соединение трех дисков тремя шарнирами

Если какое-то из указанных правил нарушается, система оказывается геометрически изменяемой или мгновенно изменяемой.

Если система образована с использованием перечисленных правил, она будет обязательно геометрически неизменяемой.

Если при кинематическом анализе в геометрически неизменяемой системе обнаруживается n избыточных связей, то система оказывается n раз статически неопределимой. При отсутствии избыточных связей система является статически определимой.

Системы, образование которых подчиняется указанным правилам, называются системами простого образования. Есть системы, порядок образования которых не может быть установлен с помощью упомянутых выше правил. Для кинематического анализа таких систем применяют иные методы, например метод замены связей, которые в настоящем пособии не рассматриваются.

3.2. Степень свободы системы

Степенью свободы системы W называется число независимых параметров, определяющих положение системы в пространстве.

Д – число дисков, из которых образована система;

Ш – число простых шарниров, соединяющих диски между собой;

С – число связей, соединяющих диски между собой;

С _О – число опорных связей, соединяющих диски с землей.

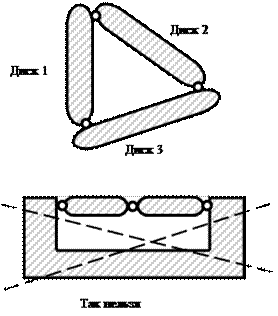
Простым шарниром называется шарнир, соединяющий два диска, такой шарнир эквивалентен двум связям. Если шарнир соединяет d дисков, то он называетсякратным шарниром и его кратность К =d–1 показывает, скольким простым шарнирам он эквивалентен (рис. 3.5).

Рис.3.5. Простой (а) и кратные (б, в) шарниры

Для произвольной плоской системы

причем диски не должны содержать избыточные связи.

Для ферм с шарнирными узлами степень свободы можно определить по более простой формуле

где У – число узлов фермы; С – число стержней фермы; С_О – число опорных связей.

Если W > 0, то система геометрически изменяемая.

Если W = 0, то система геометрически неизменяемая и статически определимая.

Важно знать, что условия геометрической неизменяемости W = 0 и W

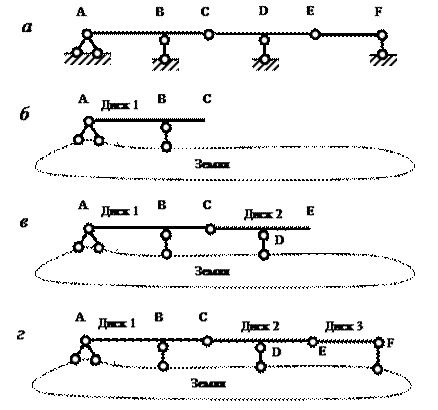
Пример 1. Кинематический анализ балки (рис. 3.6, а).

Балка собирается в такой последовательности:

1-й этап. К земле, как к диску, присоединяется Диск 1 (стержень АВС) с помощью трех связей (правило 2, рис. 3.6, б).

Рис.3.6. Последовательность сборки балки

2-й этап. К образовавшейся системе «Земля + Диск 1», как к единому диску, присоединяется Диск 2 (стержень CDE ) с помощью шарнира С и опорной связи в точке D (вариант правила 2, рис. 3.6, в).

3-й этап. К образовавшейся системе «Земля + Диск 1 + Диск 2», как к единому диску, присоединяется Диск 3 (стержень EF ) с помощью шарнира E и опорной связи в точке F (вариант правила 2, рис. 3.6, г). Этим и заканчивается сборка балки.

Поскольку образование балки (рис. 3.6, а) подчиняется установленным правилам и дополнительных (избыточных) связей не обнаружено, то заданная система является геометрически неизменяемой и статически определимой (ГН СО ).

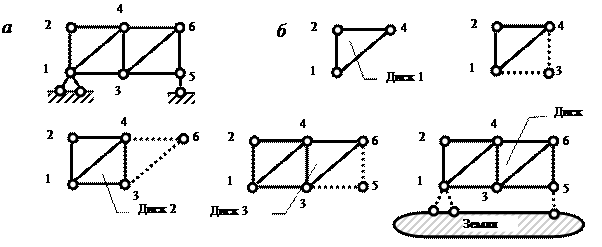
Пример 2. Кинематический анализ фермы (рис. 3.7, а).

Ферма собирается в такой последовательности:

1-й этап. Три стержня (1-2, 2-4, 1-4), как три диска, соединяются тремя шарнирами (1, 2, 4) согласно правилу 3.

2-й этап. К образовавшемуся Диску 1 (1-2-4) присоединяется узел 3 с помощью стержней 1-3 и 4-3 согласно правилу 1.

3-й этап. К образовавшемуся Диску 2 (1-2-4-3) присоединяется узел 6 с помощью стержней 4-6 и 3-6 согласно правилу 1.

4-й этап. К образовавшемуся Диску 3 присоединяется узел 5 с помощью стержней 3-5 и 6-5 согласно правилу 1.

5-й этап. Полученная ферма присоединяется к земле тремя опорными связями согласно правилу 2.

Рис.3.7. Последовательность сборки фермы: а — ферма; б — этапы сборки

Поскольку образование фермы (рис. 3.7, а) подчиняется установленным правилам и дополнительных (избыточных) стержней не выявлено, то заданная система – геометрически неизменяемая и статически определимая (ГН СО ).

Ферма может быть собрана и в иной последовательности, но в любом случае вывод будет тем же.

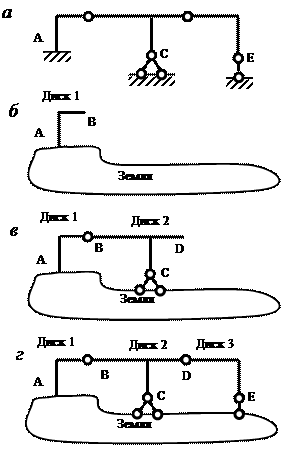
Пример 3. Кинематический анализ рамы (рис. 3.8, а).

Рама собирается в такой последовательности:

1-й этап. К земле прикрепляется стержень АВ (Диск 1 на рис. 3.8, б) с помощью жесткого защемления, которое эквивалентно трем связям (правило 2).

Рис.3.8. Последовательность сборки рамы

2-й этап. К образовавшейся системе «Земля + Диск 1» присоединяется диск 2 (стержень BCD) с помощью шарнира B и двух связей в точке С (рис. 3.8, в).

По правилу 2 достаточно в точке С иметь одну связь, поэтому вторая связь является избыточной.

3-й этап. К получившейся системе «Земля + Диск 1+ Диск 2» присоединяется диск 3 (стержень DE на рис. 2.8, г) с помощью шарнира D и опорного стержня в точке Е (правило 2).

Поскольку образование рамы (рис. 3.8, а) подчиняется установленным правилам и выявлена одна избыточная связь, то заданная система – геометрически неизменяемая и один раз статически неопределимая (ГН СН).

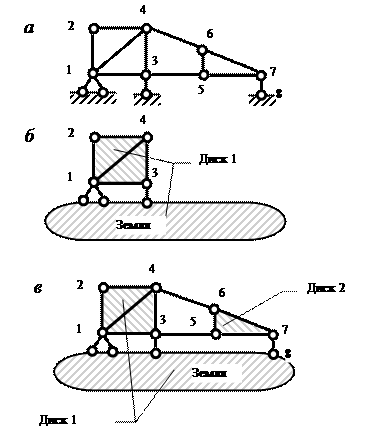
Пример 4. Кинематичес­кий анализ фермы (рис. 3.9, а).

Ферма собирается в такой последовательности.

1-й этап. Из трех стержней (1-2, 2-4, 1-4) образуется диск – треугольник 1-2-4 (правило 3), к которому прикрепляется узел 3 (правило 1) стержнями 1-3 и 4-3. Полученный диск 1-2-4-3 соединяется с землей тремя опорными связями (правило 2), образуя Диск 1 (рис. 3.9, б).

2-й этап. Три стержня (5-6, 6-7, 5-7) образуют по правилу 3 Диск 2 (рис. 3.9, в).

3-й этап. Диск 2 соединяется с Диском 1 тремя связями (4-6, 3-5, 7-8), но так как все эти связи пересекаются в одной точке 7, то правило 2 нарушается. Возможен взаимный поворот Диска 1 и Диска 2 относительно узла 7 на бесконечно малый угол.

Рис.3.9. Последовательность сборки фермы

Ввиду нарушения правила 2 заданная система является мгновенно изменяемой и не может служить расчетной схемой сооружения.

Пример 5. Найти степень свободы балки (см. рис. 3.6, а).

Балка состоит из трех дисков (стержней) AC , CE , EF , соединенных между собой двумя простыми шарнирами С и Е и прикрепленных к земле пятью опорными связями. Поэтому Д = 3, Ш = 2, С = 0, С_О = 5 и по формуле (1) получаем W = 3·3 – 2·2 – 0 – 5 = 9 – 9 = 0, что является необходимым признаком геометрически неизменяемой и статически определимой системы. Этот вывод подтверждается в примере 1.

Пример 6. Найти степень свободы фермы (см. рис. 3.7, а).

Будем использовать формулу (1) и считать каждый стержень фермы диском, т. е. Д = 9. Шарниры 2 и 5 соединяют по два стержня фермы, поэтому они простые. Шарниры 1 и 6 соединяют по три стержня фермы, поэтому они двухкратные . Шарниры 3 и 4 – трехкратные. Общее число простых шарниров Ш = 2·1 + 2·2 + 2·3 =12. Опорных связей – три.

Получаем W = 3·9 – 2·12 – 3 = 27 – 27 = 0.

При использовании формулы (2) имеем С = 9, У = 6, С_О = 3.

Получаем W = 2·6 – 9 – 3 = 12 – 12 =0.

Этот пример демонстрирует преимущество формулы (2) перед формулой (1). Признак ГН СО системы подтверждается в примере 2.

Пример 7. Найти степень свободы рамы (см. рис. 3.8, а).

Рама состоит из трех дисков AB , BCD и DE , соединенных между собой двумя простыми шарнирами B и D . К земле рама прикрепляется шестью опорными связями (три в жесткой заделке А , две в опоре С, одна в опоре Е). Поэтому Д = 3, Ш = 2, С = 0, С_О = 6 и по формуле (1) получаем

W = 3·3 – 2·2 – 0 – 6 = –1, что является необходимым признаком ГН СН системы. Этот вывод подтверждается в примере 3.

Пример 8. Найти степень свободы фермы (см. рис. 3.9, а).

При использовании формулы (2) имеем С = 10, У = 7, С_О = 4.

Получаем W = 2·7 – 10 – 4 = 14 – 14 =0, что указывает на ГН СО систему. Однако анализ образования фермы (см. пример 4) приводит к выводу о мгновенной изменяемости системы. Этот пример демонстрирует недостаточность вычисления степени свободы системы по формуле для окончательного вывода о виде системы.

Пример 9. Кинематический анализ системы (рис. 3.10, а).

Система состоит из трех дисков Д 1 , Д2 и Д3, которые соединяются между собой пятью связями 1…5. Диски Д1 и Д3 прикреплены к земле шарнирно-неподвижными опорами А и В, каждая из которых эквивалентна двум опорным связям. Поэтому Д = 3, Ш = 0, С = 5, С_О = 4 и по формуле (1) получаем

W = 3·3 – 2·0 – 5 – 4 = 9 – 9 = 0.

Система собирается в такой последователь­ности:

1-й этап. Диски Д2 и Д3 соединяются связями 3, 4, 5 по правилу 2 и образуют новый диск Д (рис. 3.10, б);

2-й этап. Три диска (Д1, Д и земля) по правилу 3 соединяются тремя шарнирами: действительными А , В и фиктивным С, не лежащими на одной прямой.

Следовательно, система – ГН СО .

Рис.3.10. Схемы к примеру 9

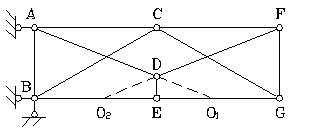
Пример 10. Кинематический анализ системы (рис. 3.11).

Для вычисления степени свободы системы по формуле (1) рассмотрим два варианта. В первом варианте считаем, что система состоит из пяти дисков – ломаных стержней ABC , ADC и прямых стержней BE , CE , DE .

Тогда шарниры A , B , D – простые, а шарниры С и Е – двухкратные .

W = 3·5 – 2·7 – 0 – 3 = 15 – 17 = –2.

Рис.3.11. Схема к примеру 10

Во втором варианте считаем, что система состоит из трех дисков – ABC , ADC и EC , которые соединяются простым шарниром А , двухкратным шарниром С и двумя связями BE и DE .

W = 3·3 – 2·3 – 2 – 3 = 9 – 11 = –2.

Замечание: нельзя считать систему состоящей только из двух дисков (ломаных стержней ABC и ADC ), так как в этом случае стержни BE , CE , DE не соединяют диски между собой.

Система собирается в следующей последовательности:

1-й этап. Диски ABC и ADC соединяются в один диск двумя шарнирами А и С, т. е. четырьмя связями, одна их которых будет избыточной (правило 2).

2-й этап. К полученному диску присоединяется узел Е тремя связями, одна их которых будет избыточной (правило 1).

3-й этап. Собранный ди ск с дв умя избыточными связями прикрепляется к земле тремя опорными связями (правило 3).

Следовательно, заданная система – ГН СН (два раза).

Пример 11. Произвести кинематический анализ системы (рис.3.12).

Определяем степень свободы системы по формуле П.Л.Чебышева :

где Д – число дисков, Ш – число простых шарниров, С₀ – количество стержней.

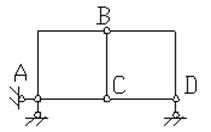
Рис.3.12. Схема к примеру 11

Отбрасывая все шарниры и опорные стержни, находим, что система состоит из пяти дисков (Д=5). Отбрасывая опорные стержни, определяем число шарниров, приведенных к простым (Ш=6: по два в точках В и С, по одному – в точках А и Д). Число опорных стержней — С ₀ =3.

Отсюда W = 3 ∙ 5 – 2 ∙ 6 – 3 = 0, то есть система может быть геометрически неизменяемой и статически неопределимой. Чтобы убедиться, что это так, выполним анализ структуры системы. Так как диски АВ, ВС и АС связаны тремя шарнирами А , В и С, не лежащими на одной прямой, то они образуют диск, к которому жестко присоединен дискВД с помощью шарнира В и стержня СД, ось которого не проходит через центр шарнира. Эта неизменяемая фигура жестко присоединена к земле с помощью трех стержней, не пересекающихся в одной точке. Таким образом, система (рис.1.14) геометрически неизменяема и не является мгновенно изменяемой.

Пример 12. Выполнить кинематический анализ системы (рис.3.13).

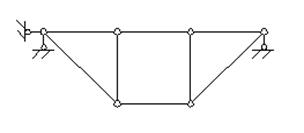
Рис.3.13. Схема к примеру 12

Так как система является шарнирно-стержневой, то для определения ее степени свободы используем формулу (2):

где У – число узлов фермы; С – число внутренних стержней; С₀ – число опорных стержней.

Здесь У =6, С=8, С₀=3, следовательно, W = 2∙6 – 8 – 3 = 1.

Таким образом, система имеет одну степень свободы, и не может использоваться как строительная конструкция.

Пример 13. Исследовать ферму (рис.3.14).

Рис.3.14. Схема к примеру 13

По формуле (2) определяем степень свободы фермы: W = 2 ∙ 7 – 11 – 3 = 0, следовательно, система может быть геометрически изменяемой и статически определимой.

Проанализируем систему. Она состоит из трех дисков – треугольники АВС, CFG и стержень DЕ, связанных между собой стержнями ВЕ, АD, ЕG, DF, которые можно заменить фиктивными шарнирами О ₁ , О₂ и шарниром С. Следовательно, можно сделать вывод: все стержни соединены между собой жестко и прикрепляются к земле так же жестко с помощью трех стержней, не пересекающихся в одной точке.

Для проверки системы на мгновенную изменяемость применим способ нулевой нагрузки – определим опорные реакции и усилия во всех стержнях при условии, что внешней нагрузки нет. Из условий равновесия всей системы ( Σ М_А = 0; Σ М_В = 0; Σ У =0) находим, что опорные реакции равны нулю. Вырезая узел Е и проектируя все силы на вертикаль, находим, что усилие в вертикальном стержне N_DЕ = 0. Затем, записывая уравнения проекций двух сил, сходящихся в узле D (третья сила — N_{D Е} = 0), на направления нормалей к этим стержням, находим, что усилия в стержнях DА и DF также равны нулю. Наконец, рассматривая равновесие узлов A, F, B, G, находим, что усилия во всех стержнях системы при отсутствии нагрузки равны нулю, следовательно, система неизменяемая.

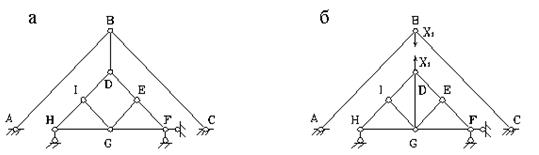
Пример 14. Выполнить кинематический анализ системы (рис.3.15,а).

Рис.3.15. Схема к примеру 14

По формуле (2) определяем степень свободы: W = 2 ∙ 9 – 11 – 7 = 0, то есть система обладает необходимым минимумом связей, чтобы быть геометрически неизменяемой. Для проверки того, является ли система действительно неизменяемой, используем метод замены стержней. Выберем заменяющую систему (рис.3.15,б). Здесь отброшен стержень ВD, а его действие заменено силами Х ₁ , и добавлен заменяющий стержень DG. Выбранная заменяющая система неизменяема: стержни АВ, ВС и земля жестко соединены тремя шарнирами, не лежащими на одной прямой. А нижняя часть системы неизменяема, поскольку состоит из треугольника (например, GHI), к которому жестко прикреплены все остальные узлы с помощью диад, и все это прикреплено к земле тремя опорными стержнями.

Теперь определим усилие в заменяющем стержне от сил Х ₁ = 1. Вырезая последовательно узлы E, I, G и рассматривая их равновесие, получим, что усилие в заменяющем стержне равно нулю, следовательно, исходная система — мгновенно изменяемая.

Пример 15. Произвести анализ образования системы, показанной на рис.3.16.

Рис.3.16. Схема к примеру 15

Вначале определяем степень свободы системы. Поскольку система является шарнирно-стержневой — воспользуемся формулой (2) W = 2У – С – С₀ . Число узлов системы У =6, число стержней системы С=8, число опорных стержней С₀=3, следовательно, W = 2 ∙ 6 – 8 – 3 = 12 — 1 = +1. Система имеет одну степень свободы и не может быть использована в качестве строительной конструкции.

Пример 16. Произвести анализ образования системы, показанной на рис.3.17, а.

Рис.3.17. Схема к примеру 16

1. Пользуясь формулой (2) W = 2У – С – С ₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =6, число стержней системы С=9, число опорных стержней С₀=3, следовательно, W = 2 ∙ 6 – 9 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть неизменяемой и статически определимой.

2. Проводим анализ структуры системы. Рассмотрим треугольник 123, который в соответствии с третьим признаком является неизменяемой системой. Считая его жестким диском (заштрихован на рис. 3.17, б), присоединим к нему двумя стержнями (3-4 и 2-4) узел 4. Эти стержни не лежат на одной прямой, следовательно, на основании первого принципа узел 4 неподвижно прикреплен к диску 123. Полученная система также является жестким диском (заштрихован на рис.3.17, в ). Прикрепив к нему двумя стержнями (4-5 и 2-5) узел 5 снова получим жесткий диск, заштрихованный на рис.3.17, г). К этому диску присоединим двумя стержнями (3-6 и 5-6) не лежащими на одной прямой последний узел 6.

Поскольку система образована в соответствии с принципами образования структурно неизменяемых систем, она неизменяема и не является мгновенно изменяемой. К земле система прикреплена так же жестко, с помощью трех опорных стержней, не пересекающихся в одной точке.

Пример 17. Произвести кинематический анализ системы, показанной на рис. 3.18.

Рис.3.18. Схема к примеру 17

1. Пользуясь формулой W = 2У – С – С ₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =9, число стержней системы С=15, число опорных стержней С₀=3, следовательно, W = 2 ∙9 – 15 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть геометрически неизменяемой.

2. Проводим анализ структуры системы. Вначале найдем заведомо неизменяемые части системы – два диска, образованные треугольниками (заштрихованы на рис. 3.18, б). Они соединены тремя стержнями. Однако эти стержни пересекаются в одной точке (т. k на рис. 3.18, б). Следовательно, система мгновенно изменяемая.

Пример 18 . Проанализировать систему, изображенную на рис. 3.19.

Система состоит из четырех дисков ( A С, С E , EF и FH ) т.е. Д=4. Число шарниров Ш = 3 (все шарниры простые). Число опорных стержней С ₀ =2+1 ∙ 4=6. Степень свободы системы по формуле W = 3Д – 2Ш – С ₀ = 3 ∙ 4-2 ∙ 3-6=0.

Рис.3.19. Схема к примеру 18

Необходимое условие неизменяемости системы удовлетворено. Производим анализ структуры. Диск АС присоединен к земле тремя опорными стержнями, не пересекающимися в одной точке. Такое прикрепление обеспечивает неподвижность диска АС. К нему шарниром С и к земле опорным стержнем в точке D прикреплен дискСЕ. При этом ось стержня D не проходит через шарнир С. К полученной неизменяемой системе стержнем EF и двумя опорными стержнями в точках G и H присоединен диск FH . Эти три стержня не пересекаются в одной точке.

Таким образом, рассматриваемая система неизменяема и не является мгновенно изменяемой.

Пример 19. Проверить геометрическую неизменяемость системы, приведенной на рис. 3.20.

Рис.3.20. Схема к примеру 19

Следовательно, система имеет необходимое количество связей, чтобы неизменяемой . Проанализируем ее структуру.

Вместе с землей система состоит из трех дисков, соединенных между собой шарниром Ш_1–2 и четырьмя стержнями, эквивалентными условным шарнирам Ш_1–3 иШ_2–3.

Так как три шарнира, соединяющие три диска, лежат на одной прямой, система мгновенно изменяема.

3.3. Степень изменяемости системы

Системы не связанные с землей

Для системы, не связанной с землей, вместо степени свободы W вводится характеристика степень изменяемости V, которую вычисляют по формулам:

V = 3Д – 2Ш – С – 3 , (3)

где смысл обозначений такой же, как в формулах (1) и (2).

Если V > 0, то система геометрически изменяемая.

Если V = 0, то система геометрически неизменяемая и статически определимая.

Условия геометрической неизменяемости V =0 и V примеры ниже).

Пример 20. Кинематический анализ системы (рис. 3.21).

C читаем, что система состоит из двух ломаных стержней ABC , CDE и четырех прямых стержней AB , BC, CD, D E.

Шарниры A и Е – простые, шарниры B и D – двухкратные , шарнир С – трехкратный.

При Д = 6, Ш = 9, С = 0 получаем

V = 3·6 – 2·9 – 0 – 3 = 18 – 21 = –3.

Рис.3.21. Схема к примеру 20

Анализируем порядок образования системы. На ломаный стержень АВС накладываются две связи АВ и ВС, которые получаются избыточными. Аналогично, избыточными являются связи CD и DE для ломаного стержня CDE . Два диска АВС и CDE соединяются только шарниром С и для использования правила 2 не достает одной связи.

Следовательно, система геометрически изменяемая, хотя и содержит три избыточные связи в отдельных своих частях. Систему можно сделать геометрически неизменяемой, если изменить расположение некоторых связей, например, заменить стержень BC на стержень BD .

Пример 21. Кинематический анализ системы (рис. 3.22).

Рама имеет два замкнутых контура, а формула (3) не допускает наличия замкнутых контуров. Поэтому разделим раму четырьмя сечениями на три части (диска), соединенных между собой тремя связями в каждом из проведенных сечений.

Рис.3.22. Схема к примеру 21

Тогда получаем Д = 3, Ш = 0,

С = 3∙4 =12 и степень изменяемости

V = 3∙3 –0 – 12 – 3 = –6.

Анализируем порядок образования системы. К среднему диску прикрепляется левый диск с помощью шести связей, три из которых являются избыточными. Затем к образованному диску присоединяется правый диск с помощью шести связей, три из которых также избыточные.

Следовательно, анализируемая система геометрически неизменяемая и содержит шесть избыточных связей.

Источник